Синтез КС из набора элементов.

Наиболее часто встречаются ситуации, когда надо строить схему не из одного типа элементов, а из набора.

Пример набора элементов:

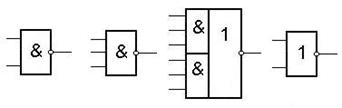
При этом возникает проблема выбора наилучшего ЛЭ на каждом этапе построения схемы. В таком случае, идеальным вариантом будет проверка реализации на каждом элементе. Но этот процесс может занять очень много времени. Для упрощения процедуры поиска оптимального ЛЭ наилучшим вариантом является сокращения их числа. Для этого используется понятие – покрываемый ЛЭ.

ЛЭ, который может быть получен из другого ЛЭ данного набора подстановкой констант на входы, называется покрываемым элементом набора.

В приведенном выше примере, из элемента 3И-2ИЛИ-НЕ путем подстановки констант можно получить ЛЭ 2И-НЕ, 3И-НЕ, 2ИЛИ-НЕ. Фактически, схему можно строить только на элементах 3И-2ИЛИ-НЕ.

При построении КС сначала используются только те ЛЭ, которые не являются покрываемыми.

Затем в построенной КС заменяем везде, где это возможно использованные ЛЭ на наиболее простые покрываемые.

При синтезе КС из непокрываемых ЛЭ остается проблема нахождения наилучшего ЛЭ в данном месте.

Всякий раз для очередной рассматриваемой функции ищем ЛЭ с minW входа. Этот элемент и надо использовать.

Если minW входа ЛЭ равны, то вычисляется суммарный вес функций входа для каждого элемента. Использоваться будет тот ЛЭ, который дает меньший суммарный вес.

При анализе ЛЭ И-ИЛИ-НЕ необходимо использовать полную дизъюнктивную модель.

Рассмотрим пример построения КС из набора элементов.

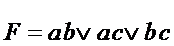
Задан набор ЛЭ.

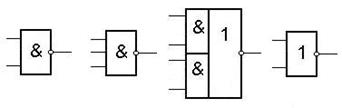
Временно исключаем из рассмотрения поглощаемые ЛЭ, и получаем сокращенный набор ЛЭ.

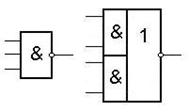
Выясним теперь, какой ЛЭ должен быть на выходе всей КС.

Предположим, что на выходе стоит ЛЭ 3И-НЕ и найдем его функции входов.

,

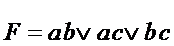
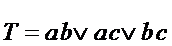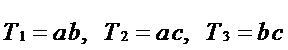
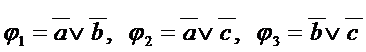
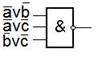
maxW = 8

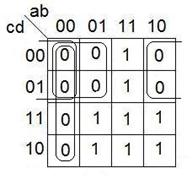
Tеперь предположим, что на выходе стоит ЛЭ 2И-2ИЛИ-НЕ и найдем его функции входов, используя неупрощенную дизъюнктивную модель.

По карте Карно находим инверсию функции и ТДНФ .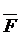

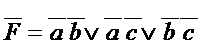
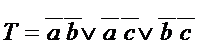
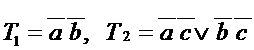
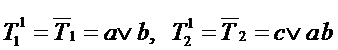
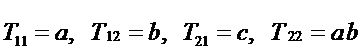
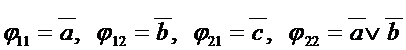
maxW = 8

Минимальный maxW у ЛЭ одинаковый. Будем выбирать по минимальному суммарному весу. Суммарный W для 3И-НЕ – 24, для 2И-2ИЛИ-НЕ – 20. Следовательно, выбираем 2И-2ИЛИ-НЕ (чем меньше вес, тем проще схема).

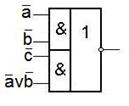
Осталось достроить функцию входа 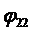. Подбираем ЛЭ для реализации 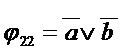(a Úb).

Анализ показывает, что здесь по минимуму maxW можно выбрать любой из двух ЛЭ. ( Сумма W для обоих ЛЭ здесь одинакова.)

Выберем И-НЕ как более простой – 3 входа вместо 4.

В итоге получаем:

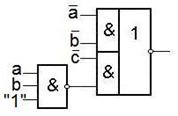
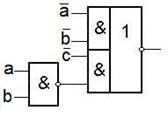
После анализа полученной схемы определяем, что ЛЭ 3И-НЕ можно заменить покрываемым элементом 2И-НЕ. Получаем окончательную схему реализации БФ.

ЛИТЕРАТУРА

1. Желенков Б.В. Дикин В.В. Курс интерактивных лабораторных работ по дисциплине «Дискретная математика». – М.: МИИТ, 2003г.

2. Першеев В.Г., Желенков Б.В. Мультимедийный конспект лекций «Дискретная математика». – М.: МИИТ, 2002г.

3. Поспелов Д.А. Логические методы анализа и синтеза схем. - М.: Энергия, 1979г.

4. Яблонский С.В. Введение в дискретную математику: Учеб. Пособие для вузов. 3-е изд.- М.: Высш. Шк., 2001 г.