Коррекция нужна из-за того, что отдельные части схемы переводятся на новые ЛЭ независимо друг от друга.

Рассмотрим пример построения схемы.

Пусть КС из И, ИЛИ, НЕ имеет вид

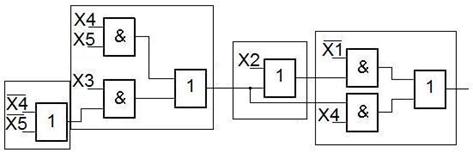
Предположим, что эта схема должна быть переведена на ЛЭ типа 3И-НЕ и 2ИЛИ-НЕ.

Перестраивая схему по частям, выделенным частям, получим:

Первая часть.

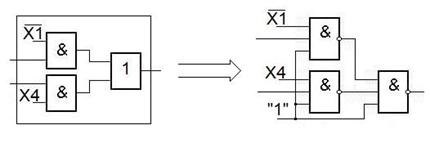
Вторая часть.

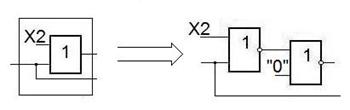
Третья часть.

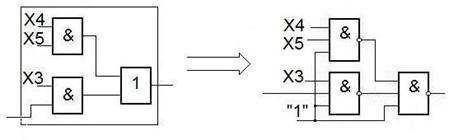
Четвертая часть.

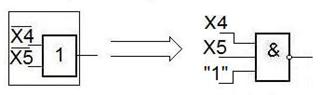
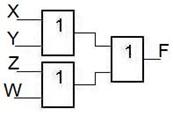
В результате получим схему следующего вида:

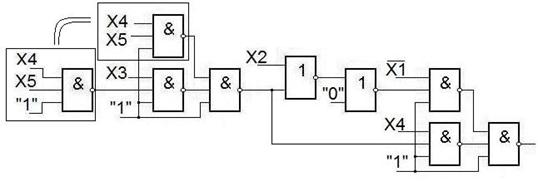
В полученной схеме содержатся общие части. После выполнения корректировки получим:

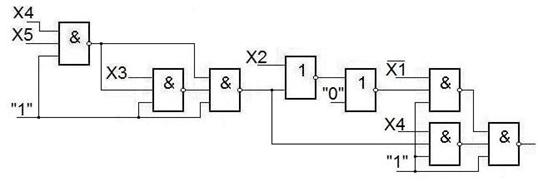
Примечание.

Исходную схему (1-ый этап) можно построить методами раздела 2.2 либо даже из других ЛЭ другими способами, а потом переводить на требуемые ЛЭ по частям.

Например, исходной может быть схема

РАЗДЕЛИТЕЛЬНЫЙ МЕТОД СИНТЕЗА

СХЕМ МИНИМАЛЬНОЙ ГЛУБИНЫ

ИЗ ЭЛЕМЕНТОВ

И-НЕ, ИЛИ-НЕ, И-ИЛИ-НЕ.

Базовая концепция.

Начинаем строить схему от выхода. Находим выходной ЛЭ и функции его входов для реализации бф F.

j₁

y F

j_k

F = y(j₁,j₂,...j_k).

Далее процедура повторяется для j₁,j₂,...j_k,пока для всех ЛЭ схемы в качестве функций входов будут получены независимые (отдельные) переменные или константы.

При этом в процессе построения схемы возникает две проблемы:

1. Выбрать «наилучший ЛЭ» из числа заданных;

2. Найти «наилучшую совокупность» функций входов ЛЭ.

Рассмотрим пример возникновения первой проблемы.

F = XYÚXZÚYWÚZW
XYÚXZÚYWÚZW = (XÚW)(YÚZ)

Рассмотрим пример возникновения второй проблемы.

F =XÚYÚZÚW
XÚ(Y(Ú(Z(ÚW)))	(XÚY)Ú(ZÚW)
Глубина схемы = 3	Глубина схемы = 2

Нужно научится, для выбранного ЛЭ, сроить совокупность функций его входов и сравнивать результаты, полученные для разных ЛЭ.

Сравнение удобно выполнять с помощью оценок (весов) реализуемых БФ. Чем точнее оценка, тем сложнее она получается. Абсолютно точная оценка по сложности эквивалентна сложности полного перебора всех вариантов построения схем.

Простейшей оценкой может быть величина n, но такая оценка очень груба. Она не позволяет различать функции с одинаковым числом переменных.

F = XÚYÚZÚW; n = 4.

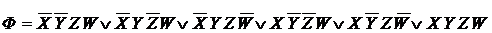; n = 4.

Наилучшим образом учитывает индивидуальные свойства функций оценка БФ, получаемая по ТДНФ (вес W для ТДНФ).

Вычисление W для ТДНФ будет рассмотрено ниже.

Проведение предварительной оценки позволяет сравнивать варианты схем без их построения.

Если W(F₁) > W(F₂), то Г(F₁) > Г(F₂)

Г(F) - глубина КС, реализующей F.

Пусть имеем некоторую схему:

j₁

y F

j_k

и пусть оценки (веса) функций входов при этом:

W(j₁), W(j₂), …W(j_K).

Таких схем может быть много. Для каждой из них получим веса.

Лучшей будет схема, в которой maxW(j_J) для J от1 до k будет как можно меньше. (maxW определяет Г.)

Наша задача – нахождение иметь min(max(W(j_J)) по разным вариантам выбора функций входов.

Любая приближенная оценка не может быть абсолютно точной, и из-за этого схема может быть не лучшей, но это плата за приемлемое время решения задачи.

Для получения функций входов ЛЭ будем пользоваться дизъюнктивными моделями ЛЭ (моделями из дизъюнкторов и инверторов).

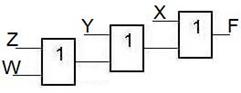
Пример модели.

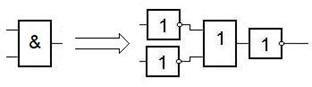
По такой модели, двигаясь от выхода ко входам, легко находить функцию входа инвертора (однозначно получается инверсией функции выхода) и функции входов дизъюнкторов ( получаются разделением ТДНФ).

Рассмотрим пример реализации функции.

ТДНФ для F имеет вид 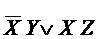. Отсюда получим:

Замена исходной ДНФ на ТДНФ, в данном примере дала упрощение функций входов и, соответственно, даст упрощение схемы их реализующей.

Но дело не только в этом.

Если разделение делать не по ТДНФ, то процедура синтеза может не сходиться (будем строить схему до бесконечности).

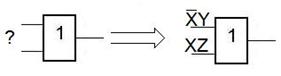
Для реализации БФ F в процессе синтеза может потребоваться реализация БФ F. ?!

Рассмотрим пример.

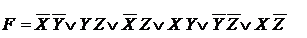
Построим карту Карно для данной функции.

Выполним поиск ТДНФ

В итоге получаем две ТДНФ.

Если начать разделение F по исходному выражению, то можно получить схему вида

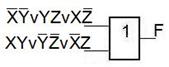
Что соответствует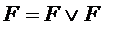

Вес W для F рассчитывается по ТДНФ этой функции.

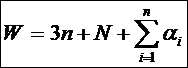
где N - число букв ТДНФ;

a_i=0, если i-ая переменная входит в ТДНФ либо только в прямом, либо только в инверсном виде, иначе a_i=1.

Рассмотрим пример.

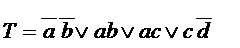
W = 3^*4 + 8 + (1 +1 + 0 + 0) =22.

Другой способ подсчета веса ТДНФ выполняется следующим образом:

Первое появление переменной вносит в вес значение – 4.

Первое появление инверсии бывшей ранее буквы – 2.

Повторное появление буквы – 1.

При выполнении суммирования этих весов получим ту же величину W. Порядок просмотра может быть любым.

Рассмотрим пример.

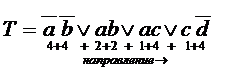
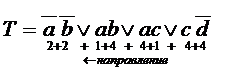
В обоих случаях W = 22.

Умея подсчитывать W, можно научиться разделять ТДНФ на части так, чтобы maxW среди весов отдельных частей был по возможности минимальным. Решив эту задачу, можно научиться строить схемы минимальной глубины по дизъюнктивным моделям ЛЭ.