При синтезе кс из элементов типа и, или, не.

Рассмотрим алгоритм построения КС с помощью скобочных преобразований.

1. Преобразуем исходную ДНФ многократно вынося за скобки переменные.

Пример.

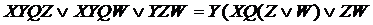
2. Выделяем одинаковые подфункции в скобочной форме F и получаем совокупность функций для F.

Пример.

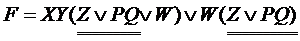
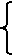F = XY(ФÚ W) Ú WФ

Ф = Z Ú PQ

3. Выделяем конъюнкции или их части общие для нескольких мест (одинаковые) и расширяем совокупность функций.

Пример.

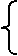F = XY(F Ú W) ÚWF Ú MNK

F = Z Ú MNP

F = XY(F Ú W) ÚWF Ú YK

F = Z Ú YP

Y = MN

При поиске и выделении общих частей конъюнкций учитывается, что выделение k букв из Lконъюнкций дает выигрыш W = k(L-1).

Выделяя общие части с максимумом W при W > 0, мы обеспечиваем упрощение схемы.

Далее по совокупности БФ строится КС, например, моделированием полученных выражений.

Действия по п.2 и 3 ясны. Действия по п.1 рассмотрим подробнее, полагая, что исходное выражение для F - ДНФ.

Исходную ДНФ, рассматриваемой БФ F, обозначим как D⁰.

Делая вынесение за скобки переменных, получим

D⁰ = K⁰&(D ⁰₁) Ú D⁰₂

КонъюнкцияДНФ

Поиск выносимых за скобки переменных (конъюнкции) рассмотрим далее.

«Убираем» на время из рассмотрения внутри-скобочное выражение для D ⁰₁ и получаем ДНФ D ¹ .

D ¹ = K⁰&(F ⁰₁) Ú D⁰₂ .

Переменная, заменяющая ДНФ D ⁰₁ .

D ¹ обрабатываем как исходную ДНФ D⁰, если возможно вынесение за скобки K¹ и представление ее в виде

D ¹ = K¹&( D ¹₁) Ú D¹₂ .

Затем аналогично получаем D ² , D ³ и т.д.

Если в D^j уже нельзя выделить К^j , то берем

D ^j = K^j-1&(F ^j-1₁) Ú D^j-1₂

и подставляем туда последовательно (D ^j-1₁) вместо F ^j-1₁, (D ^j-2₁) вместо F ^j-2₁ и т.д. до (D ⁰₁) вместо F ⁰₁.

При этом мы получаем выражение, в котором в скобки заключены ДНФ D ⁰₁, D ¹₁, …D ^j-1₁.

Каждую из этих ДНФ будем обрабатывать как исходную, продолжая до тех пор, пока это возможно.

В результате получим искомую форму.

Рассмотрим пример.

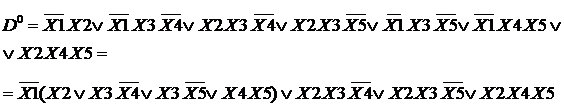
К⁰ D ⁰₁ D⁰₂

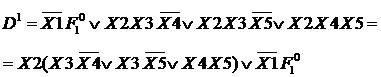
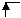К¹ D¹₁ D¹₂

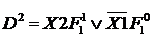
Дальнейшее вынесение за скобки невозможно.

Подставляя всюду D^q₁ вместо F ^q₁, получаем

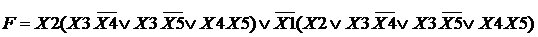
Преобразуя каждую ДНФ из скобок, получим

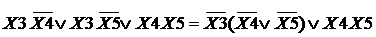
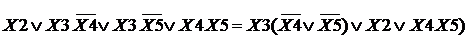
Полученные здесь в скобках ДНФ уже не допускают дальнейших скобочных преобразований.

Заменив преобразованные ДНФ на скобочные выражения, получим

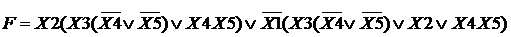
На этом скобочные преобразования завершены.

Выделив одинаковые подфункции, мы получим

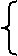
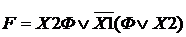
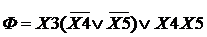
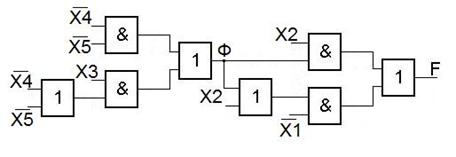
В результате, получаем схему.

Замечание о многовыходных схемах.

Для системы БФ, каждая функция приводится к скобочной форме отдельно. Затем во всех функциях находятся одинаковые части формул и конъюнкций и формируется общая совокупность функций.

Следует отметить, что при большом числе «похожих» конъюнкций в разных БФ, лучшие результаты может дать другой подход.

1) В совокупности всех БФ выделяются общие части и заменяются новыми переменными;

2) БФ (с новыми переменными, если они введены) раздельно обрабатываются описанным ранее способом;

3) Введенные в 1) переменные реализуются схемами.

При синтезе многовыходных схем удобно строить схемы, используя поочередно оба подхода, и выбирать лучшую.

Выясним теперь, как в днф D ^j найти конъюнкцию K^j, чтобы, вынеся ее за скобки, получить D ^j = K^j&( D ^j ₁) Ú D^j₂

Обозначим (Kⁱ)_J совокупность первых j букв в Kⁱ.

Весом W(Kⁱ)_J для (Kⁱ)_J назовем

W[(Kⁱ)_J ] = j^. (L_k-1),

где L_k - число конъюнкций в D ⁱ, содержащих (Kⁱ)_J.

Kⁱ строим, последовательно находя (Kⁱ)₁, (Kⁱ)₂, …так, чтобы вес W для (Kⁱ)_J всякий раз был наибольшим и больше нуля.

Переходя к (Kⁱ)_J нужно подобрать к (Kⁱ)_J-1 такую переменную, чтобы вес (Kⁱ)_J был наибольшим.

Отбор переменных к (Kⁱ) идет до тех пор, пока вес (Kⁱ)_J не начнет убывать.

Рассмотрим пример.

Dⁱ = X1X2X3ÚX1X2X4ÚX1X5ÚX2X5

	X1	W=2 - max	(Ki)1 = x1
	X2	W=2
(Ki)1 =	X3	W=0
	X4	W=0
	X5	W=1
	X1X2	W=2 - max	(Ki)2 = X1X2
(Ki)2 =	X1X3	W=0
	X1X4	W=0
	X1X5	W=0
	X1X2X3	W=0
(Ki)3 =	X1X2X4	W=0
	X1X2X5	W=0

В итоге получаем

Dⁱ = X1X2(X3ÚX4)ÚX1X5ÚX2X5

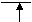Кⁱ Dⁱ₁ Dⁱ₂

Схема, построенная по этому выражению, будет содержать 4 двухвходовых конъюнктора.

Схема для исходной ДНФ содержит 6 двухвходовых конъюнкторов.

Вес W для Kⁱ равен числу конъюнкторов, которые могут быть удалены из КС для ДНФ D ⁱ после перехода к КС для D ⁱ в виде

D ⁱ = Kⁱ&( D ⁱ₁) Ú Dⁱ₂

СИНТЕЗ КС ИЗ ЭЛЕМЕНТОВ

И-НЕ, ИЛИ-НЕ, И-ИЛИ-НЕ.

КС часто используемых БФ.

Наиболее часто используемыми БФ являются конъюнкция, дизъюнкция, сумма «по модулю 2» и инверсия.

F = X1&X2& … &Xn

F = X1ÚX2Ú… ÚXn

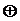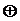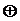F = X1 X2 … Xn

F = X1oX2o…oXn

где o - либо &, либо Ú ,либо .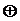

Существует набор стандартных решений для построения БФ.

Для этого используются следующие правила:

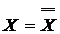
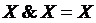
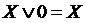
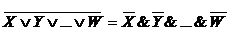
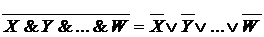
Для &, 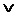и 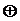имеется свойство ассоциативности:

возможность произвольной расстановки скобок в формуле

F = X1oX2o…oXn

Например:

F = X1oX2o…oXn = X1o(X2(o…oXn))= (X1oX2)o(…oXn)

В зависимости от того, как расставляются скобки, можно получить выражение, задающее КС последовательной, пирамидальной или смешанной структуры.

Последовательная структура.

;

N- число переменных; К - число входов ЛЭ;

Г - глубина КС; S - число ЛЭ в КС.

Пирамидальная структура.

,

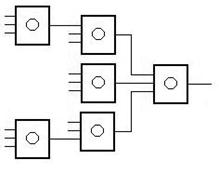
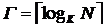Смешанная структура.

Мы увидели, как построить КС с n входами из ЛЭ (либо «блоков») с К входами, реализующими такие же функции, что и вся КС. Обратимся теперь к построению «блоков».

Рассмотрим типы используемых ЛЭ и их обозначения.

ЛЭ И-ИЛИ-НЕ таков, что из него путем подстановки констант или отождествления входов можно получать ЛЭ типа И-НЕ либо ИЛИ-НЕ.

Покажем это.

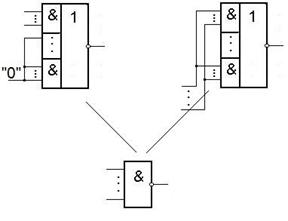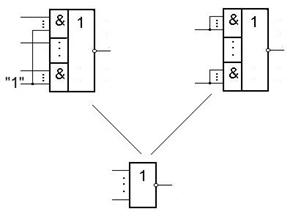Рассмотрим способы получения инверторов из элементов И-НЕ, ИЛИ-НЕ, И-ИЛИ-НЕ.

Рассмотрим способы получения конъюнкции из элементов И-НЕ, ИЛИ-НЕ, И-ИЛИ-НЕ.

Получение конъюнкции из элементов И-НЕ.

Получение конъюнкции из элементов ИЛИ-НЕ.

Получение конъюнкции из элементов И-НЕ и ИЛИ-НЕ.

Получение конъюнкции из элементов И-ИЛИ-НЕ.

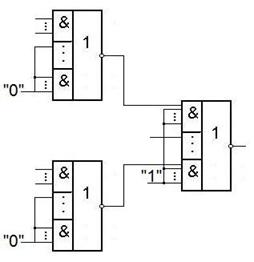
Рассмотрим примеры получения конъюнкций.

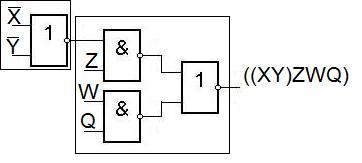
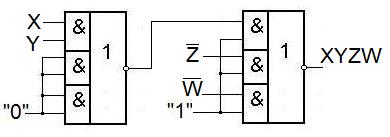
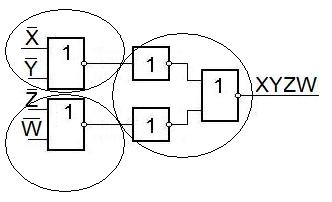
Получение дизъюнкции из элементов ИЛИ-НЕ.

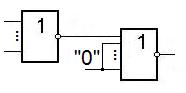
Получение дизъюнкции из элементов И-НЕ и ИЛИ-НЕ.

Получение дизъюнкции из элементов И-ИЛИ-НЕ.

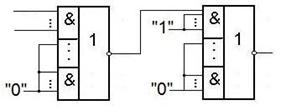
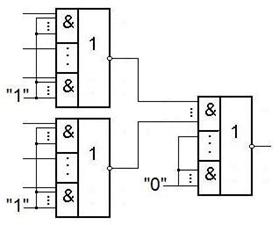
Рассмотрим примеры получения дизъюнкций.

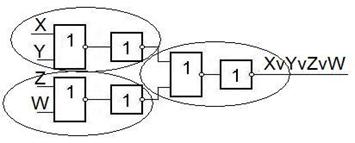
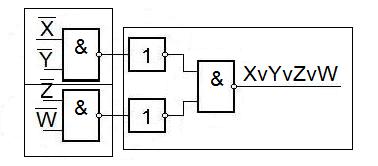
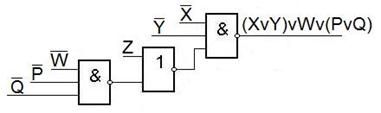
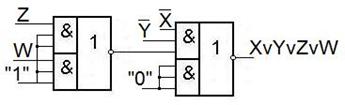
Теперь рассмотрим схемы для получения суммы по модулю два.

X	Y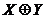

В соответствии с таблицей истинности можно получить несколько способов реализации этой функции.

Первый способ – на элементах И-НЕ.

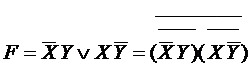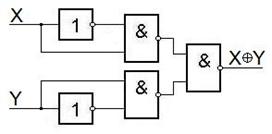Второй способ – на элементах ИЛИ-НЕ.

Третий способ – на элементе И-ИЛИ-НЕ.

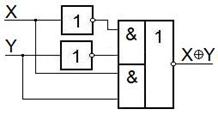Рассмотрим использование выражений вида И-ИЛИ.

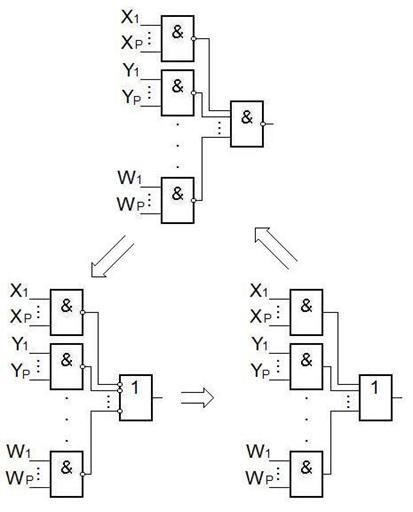
F=(X₁&…&X_P) (Y₁&…&Y_P) … (W₁&…&W_P)

Рассмотрим примеры реализации выражений И-ИЛИ.

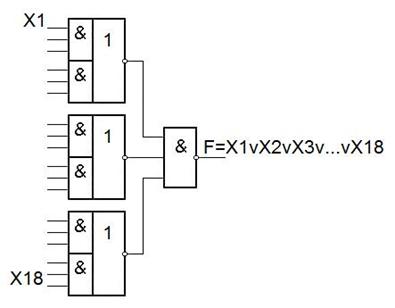
КС ДЛЯ ПРОИЗВОЛЬНЫХ БФ.

Процедура построения КС состоит из трех этапов:

1. Строится схема из элементов И, ИЛИ, НЕ.

2. Отдельные части схемы вида И-ИЛИ, либо И, либо ИЛИ переводятся в схемы из заданных ЛЭ (см. раздел 2.3.1).

3. Полученная КС корректируется с целью устранения возможной избыточности, например, вида

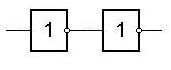
или нахождения общих частей.