Построение ТДНФ недоопределенных БФ.

Есть много методов удаления из ДНФ избыточных конъюнкций. Наиболее просты табличные, наиболее точны - аналитические.

К числу простейших способов преобразований относится последовательное использование законов поглощения и обобщенного склеивания.

Рассмотрим пример.

Можно при поиске ТДНФ (или близких к ним ДНФ) использовать таблицы покрытий, размечая столбцы конъюнкциями из исходной D₁, а строки совокупностью простых импликант, построенных по D₁.

На практике столбцы удобно размечать кодами конъюнкций из исходной D₁, ставя метку в клетке (i,j), если K_i = 1 после подстановки в нее константных значений из кода конъюнкции j-ого столбца.

Процедура поиска ТДНФ по таблице покрытий рассматривалась ранее (если исходная ДНФ D₁ была представлена ДСНФ, то ее коды фактически совпадают с наборами из М₁ и наша таблица в точности совпадает с таблицами покрытий, рассматривавшимися ранее).

Рассмотрим пример.

D₁^исх =

D₁ =

	0-00					0-11
	*	*	*				«ядро»
		*	*			*	«ядро»
		*		*
				*	*		«ядро»

F =

Наиболее хорошие результаты можно получить, если столбцы размечать отдельными наборами из М₁, но их не всегда можно построить по исходной ДНФ D₁ из-за того, в М₁ их может быть слишком много.

Карты Карно.

Рассмотрим принципы визуальных методов минимизации БФ (карты Карно, диаграммы Вейча, графы и др.).

Множество всех наборов значений переменных представляется специальной фигурой.

Конъюнкция представляется наглядным графическим образом, легко обнаруживаемым на используемой специальной фигуре (правильная конфигурация.)

Поиск ДНФ - визуальный поиск покрытия области М₁ по правильными конфигурациями.

Поиск покрытия в основном за интуицией человека!

Рассмотрим функцию от двух переменных (n =2).

Фигура, представляющая множество всех наборов значений переменных - плоскость.

На плоскости - прямоугольная таблица, каждая клетка которой представляет набор значений переменных.

X Y			Клетки размечаются значениями функции	X	Y	F

В таблице выделяется прямоугольник из соседних клеток, число которых равно целой степени двух (правильная конфигурация) и функция в них принимает значение «1».

Код конъюнкции – набор значений переменных, описывающих клетки правильной конфигурации. Переменная, чье значение сохраняется неизменным во всех клетках конфигурации отображается в коде эти значением, остальные переменные - прочерком «-».

Конъюнкция получается по ее коду.

Рассмотрим пример.

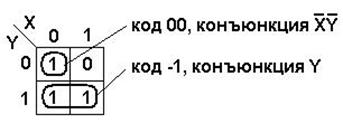
Рассмотрим карту Карно для функции от трех переменных (n =3).

Фигура, представляющая множество всех наборов значений переменных - развертка цилиндра (есть соседства через левый и правый край).

Примеры правильных конфигураций.

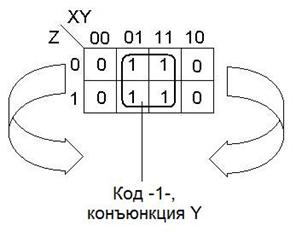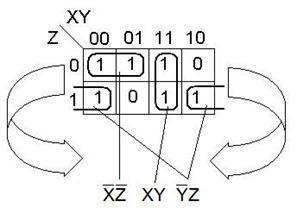
Примеры «неправильной» конфигурации.

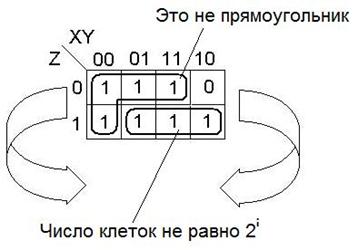
Рассмотрим карту Карно для функции от четырех переменных (n =4).

Фигура для всех наборов значений переменных - развертка тора (есть соседства через все края).

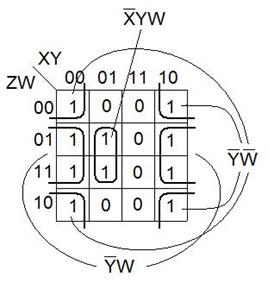Поиск ДНФ сводится к поиску покрытий М₁ по правильным конфигурациям.

Рассмотрим примеры.

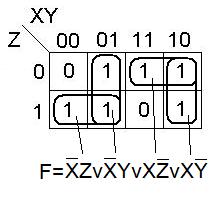
Данную функцию можно представить в более коротком виде.

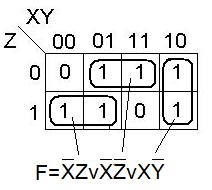
Пример нахождения ДНФ для функции от 4-х переменных.

При построении ДНФ по карте Карно, критерием является ранг покрытия - число букв задаваемой им ДНФ. Наш задача – получить минимум.

Простая импликанта имеет образ правильной конфигурации, не являющейся частью одной другой.

Пример простой импликанты.

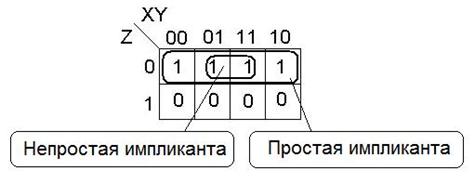
Для недоопределенной БФ F_~ строится покрытие, у которого М₁ М_~ ММ₁

Все «единицы» должны быть покрыты и, при этом, могут быть покрыты клетки с «~», то есть клетки области неопределенности. Это позволяет уменьшить количество букв в ДНФ.

Рассмотрим пример.

Примечание.

Для нахождения МДНФ - области покрытия должны быть максимально возможными, а количество областей и их пересечение необходимо свести к минимуму.

Для нахождения СДНФ - области должны быть максимально возможными, должны быть представлены все возможные области (максимальное количество пересечений областей).

Рассмотрим пример нахождения СДНФ по карте Карно.

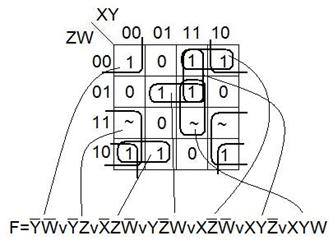
Рассмотрим пример нахождения МДНФ по карте Карно.

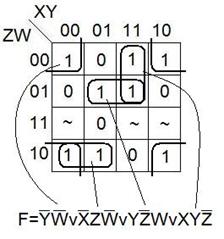
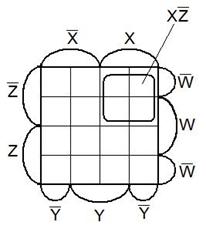
Карты (диаграммы) Вейча строятся аналогично картам Карно.

Правильная конфигурация здесь описывается конъюнкцией. По конъюнкции можно получить ее код, а затем по коду можно получить ее М₁.

(В картах Карно наоборот - по наборам получается код конъюнкции, а по коду сама конъюнкция.)

ЛОГИЧЕСКИЕ СХЕМЫ (ЛС).

ОСНОВНЫЕ ПОНЯТИЯ.

ЛС - это физические объекты, имеющие n входов и m выходов.

n ЛС m

На входы поступают сигналы, представляющие значения дискретных переменных. На выходах ЛС формируются сигналы -реакции на входные воздействия.

Чаще всего сегодня используются электрические сигналы, которые представляют двоичные переменные. «1» представляется высоким уровнем напряжения, например, +5 вольт, а «0» - низким уровнем, например, 0 вольт.

В ЛС закон, устанавливающий соответствие между реакцией и входным воздействием, можно описать БФ.

Это значит, что в любой момент времени набор значений двоичных переменных, представленный входными сигналами, однозначно определяет набор значений переменных, представленных выходными сигналами.

ЛС строятся из более мелких ЛС (неделимых в рамках рассмотрения), называемых логическими элементами (ЛЭ).

Процедура получения ЛС из ЛЭ заключается в том, что входы всех ЛЭ присоединяются либо к выходам других ЛЭ, либо к выходам источников входных сигналов.

Выходы некоторых лэ должны быть отмечены как выходы ЛС.

Все входы и выходы ЛЭ должны использоваться.

На вход любого ЛЭ не должен поступать сигнал, сформированный на выходе того же лэ. (Результат не должен зависеть сам от себя.) Иначе ЛС некорректна.

Рассмотрим пример некорректной ЛС.

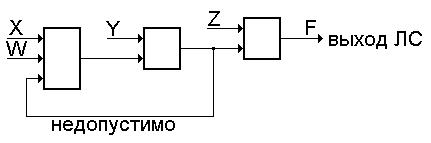
Набор ЛЭ должен обладать свойством функциональной полноты - обеспечивать возможность построения из них ЛС, реализующих любые БФ.

К числу таких относятся ЛЭ, реализующие БФ:

- И, ИЛИ, НЕ - базовый теоретический набор;

- И-НЕ ( ) - элементы Шеффера;

- ИЛИ-НЕ ( 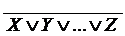) - элементы Пирса;

- и др.

Задача синтеза ЛС состоит в получении схемы из заданного набора ЛЭ. При этом можно говорить о схеме:

- с минимумом числа лэ;

- с минимумом числа последовательно соединенных лэ;

- с какими-то другими критериями качества;

- без использования критериев качества.

Простейший прием синтеза ЛС состоит в моделировании формулы, реализуемой БФ, схемой из заданных БФ.

Для этого нужно уметь строить схемы для БФ всех операций формулы.

Если БФ ЛЭ непосредственно реализуют операции, используемые в формуле, задача упрощается.

Рассмотрим пример.

Дано: F =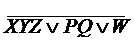

Набор ЛЭ:

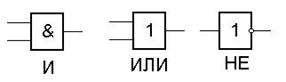
Построить ЛС, реализующую F из заданного набора ЛЭ.

Строим схему от выхода!

Если бы набор ЛЭ был другим, то для той же самой БФ, ЛС изменится.

Набор ЛЭ:

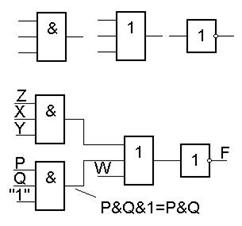
Формулу всегда можно представить ЛС, но есть ЛС не представимые формулой.

Это такие ЛС, в которых есть ЛЭ с выходами, идущими к нескольким ЛЭ.

Пример.

Эту ЛС можно описать аналитически совокупностью БФ вида:

F = F₁Ú F₂

F₁ = A& F₃ Такой прием пригоден

F₂ = D& F₃ для любой ЛС.

F₃ = B Ú C

Выполнив подстановки, мы получим

F = (A&(BÚC)) Ú (D&(BÚC)).

Построив по этой формуле ЛС, получим

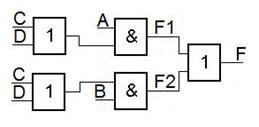
Полученная ЛС не совпадает с исходной (сложнее).

Данный пример показывает, как получить аналитическое описание БФ в виде совокупности БФ для ЛС. Так (совокупностью БФ) можно описать любую ЛС.

Переходя от совокупности БФ к формуле, можно получить описание более сложной ЛС.

Формула не позволяет описывать ЛС, в которой объединены одинаковые части схемы.

Однако, имея формулу, можно получить по ней совокупность БФ, описывающую ЛС с объединенными одинаковыми частями схемы. (Этим объясняется наш интерес к формулам.)

В заключение отметим, что в настоящее время ЛС чаще всего называют комбинационные схемы, подчеркивая тем самым, что реакция схемы определяется комбинацией значений входных сигналов. Комбинационные схемы (КС) - термин, который мы будем использовать в дальнейшем.

ИСПОЛЬЗОВАНИЕ СКОБОЧНЫХ ПРЕОБРАЗОВАНИЙ ДНФ