Вероятность суммы несовместных событий

Ø Суммой событий А₁, А₂, ..., А_n называется событие А = А₁+А₂+ ...+ А_n, состоящее в наступлении хотя бы одного из событий А₁, А₂,...,А_n.

Например, два стрелка стреляют в одну и ту же мишень по одному разу. Обозначим события:

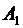: {1-й стрелок попал в мишень},

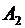: {2-й стрелок попал в мишень}.

Тогда их суммой будет следующее событие А: {мишень поражена}, то есть попал либо только 1-й стрелок, либо только 2-й, либо попали оба.
Если события А₁, А₂, ..., А_n несовместны, т.е. одновременно они наступить не могут, то определение будет следующим.

Ø Суммой несовместных событий А₁, А₂, ..., А_n называется событие А, состоящее в наступлении только одного из событий А₁, А₂, ..., А_n в одном и том же испытании.

Например, события « идет дождь» и «светит солнце» – совместны.

Теорема 3.Вероятность суммы несовместных событий равна сумме их вероятностей.

.

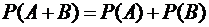Формула допускает обобщение на любое число попарно несовместных событий.

Примеры.

1.Брошены две игральных кости. Какова вероятность, что сумма очков на выпавших гранях будет не меньше 10?

Решение. В данном испытании фраза «не меньше 10» означает, что выпадет 10 или 11, или 12 очков. Все три эти события несовместны, поэтому вероятность их суммы равна сумме вероятностей. Из 36 исходов 3 будут благоприятствовать выпадению 10 очков. Это: (4,6); (5,5) и (6,4). 11 очков могут выпадать двумя способами: (5,6) и (6,5), а 12 очков – только одним способом. Итак, если обозначить:

– А: {выпадение в сумме 10 очков};

– В: {выпадение в сумме 11 очков};

– С: {выпадение в сумме 12 очков};

– D: {выпадение не меньше 10 очков},

то 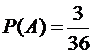, , 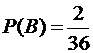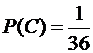. По теореме 3 получим

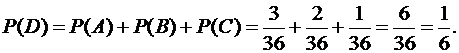
Ответ: 1/6.

2. В ящике 8 радиодеталей, из которых 3 – стандартные. Определить вероятность того, что среди двух наудачу извлеченных деталей, хотя бы одна – стандартная.

Решение. Пусть событие А: {одна деталь стандартная}, событие В: {две детали стандартные}. Тогда событие 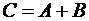: {хотя бы одна из двух деталей – стандартная}. Так как события А и В несовместные, то по теореме сложения вероятностей имеем:

.

; .

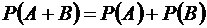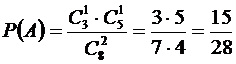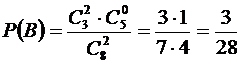Итак,

.

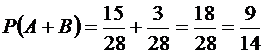Ответ: 9/14.

3.В партии из 10 деталей 8 – стандартных. Найти вероятность того, что среди наудачу извлеченных 3-х деталей есть хотя бы одна стандартная.

Решение. Пусть событие А: {из трех деталей одна стандартная}, В:{из трех деталей две стандартные}, событие С: {все три детали стандартные}. Тогда событие Е = А + В + С : {среди трех деталей есть хотя бы одна стандартная}. Так как события А, В, С несовместны, то имеем: 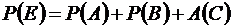. Найдем 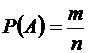, где n – число всевозможных извлечений трех шаров из 10 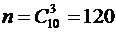, а m – число благоприятствующих исходов, то есть из трех деталей будет одна стандартная и две нестандартных. 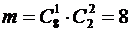. Тогда .

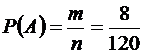Аналогично, ; .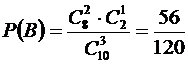

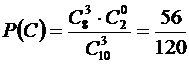Тогда .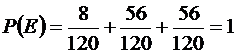

Ответ: 1.

4.Вероятность выхода изделия из строя при эксплуатации сроком до одного года равна 0,13, а при эксплуатации сроком до 3 лет – 0,36. Найти вероятность выхода из строя изделия при эксплуатации сроком от 1до 3 лет.

Решение. Пусть событие А: {выход из строя изделия сроком эксплуатации до 1 года}; событие В: {выход из строя изделия, сроком эксплуатации до 3 лет}; событие С: {выход из строя изделия, сроком эксплуатации от 1 до 3 лет}.

Тогда событие 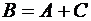. Так как события А и С несовместны, то имеем 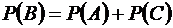. Откуда получим:

.

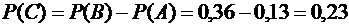Ответ: 0,23.

5.Товар завозится в магазин с трех баз. Вероятности того, что нужный товар находится на первой, второй и третьей базах равны соответственно: 0,6; 0,7; 0,8. Найти вероятность того, что нужный товар есть: а) только на одной базе; б) не менее, чем на двух базах.

Решение. Событие 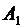: { нужный товар есть на первой базе}, 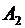: { нужный товар есть на второй базе}, 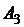: { нужный товар есть на третьей базе} Тогда событие 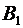: {наличие товара только на одной базе}, будет равно сумме несовместных событий 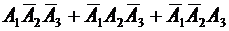(товар есть только на одной базе).

Пусть событие 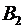: {наличие товара только на двух базах}, тогда .

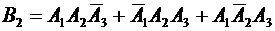Cобытие 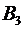: {товар есть на всех трех базах}, тогда .

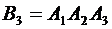По условию задачи, Р(А₁) = 0,6; Р(А₂) = 0,7; Р(А₃) = 0,8. Вероятности противоположных событий:

; ; ,

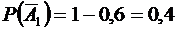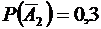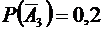а) вероятность того, что товар есть только на одной базе, равна 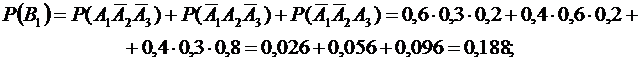б) наличие товара не менее, чем на двух базах означает, что он может быть либо на двух базах, либо на всех трех. События 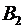и 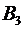несовместны, тогда:

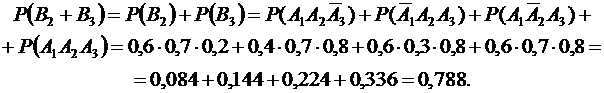
Ответ: а) 0,188; б) 0,788.