Выделение областей устойчивости с помощью D – разбиения

Метод D – разбиения пространства по одному или двум параметрам позволяет анализировать на плоскости устойчивость систем автоматического регулирования в зависимости от их изменения.

При разбиении пространства по одному параметру 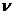характеристическое уравнение замкнутой системы записывается в виде:

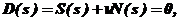(5.1)

где S(s) – полином, не зависящий от ,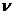

N(s) – полином, содержащий 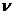множителем.

Приняв 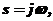найдем границу D – разбиения

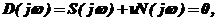(5.2)

откуда

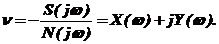(5.3)

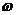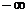Изменяя от до 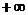построим в плоскости 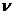кривую, отображающую мнимую ось плоскости корней характеристического уравнения s на плоскость 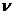, т.е. границу D – разбиения. Граница D-разбиения делит плоскость параметра 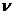на области с одинаковым числом правых корней. Эти области принято обозначать 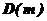, где 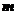обозначает число правых корней характеристического уравнения.

При построении границы D – разбиения достаточно построить её для положительных значений частоты 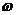и затем дополнить зеркальным отображением построенного участка относительно действительной оси.

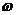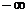Если при изменении от до 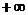в плоскости корней характеристического уравнения 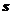двигаться по мнимой оси и штриховать её слева (рисунок 2.3а), то такому движению в плоскости параметра 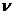соответствует движение по границе D – разбиения.

Для того, чтобы решить вопрос о выделении области устойчивости, кривую D – разбиения необходим заштриховать по определённым правилам.

Правило штриховки

При перемещении вдоль кривой D – разбиения от точки 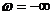к точке 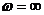её следует всегда штриховать слева (рисунок 2.3б). Это соответствует тому, что если перемешаться в плоскости корней S – вдоль мнимой оси от 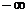до 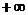, то область, где корни имеют отрицательные вещественные части, находиться всё время слева (рисунок 2.3а).

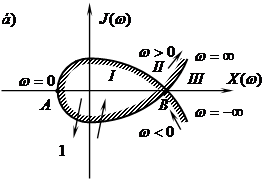Рисунок 5,1 – Штриховка мнимой оси плоскости корней характеристического уравнения s и кривой D-разбиения плоскости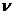

Претендентом на область устойчивости является область, внутрь которой направлена штриховка и которой поэтому соответствует область с наибольшим числом левых корней. На рисунке 2.3б это область I.

Чтобы установить, является ли эта область действительно областью устойчивости, необходимо задаться каким – либо значением 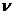, лежащим в этой области. Подставив его в характеристическое уравнение, нужно установить все ли корни характеристического уравнения при этом будут левыми, пользуясь любым критерием устойчивости.

Если окажется, что система не устойчивая, то области устойчивости нет, т.е., изменяя только параметр 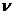, нельзя сделать систему устойчивой.

Учитывая, что изменяемый параметр является вещественным числом, из полученной области устойчивости выделяется только отрезок устойчивости, т.е. отрезок вещественной оси, лежащий в области устойчивости (например, отрезок AB на рисунке 2.3б).

Допустим, I является областью устойчивости. Так как для устойчивых систем характеристическое уравнение не имеет правых корней (m=0), обозначим ее D(0).

Для определения числа правых корней в других областях пользуются правилом: если происходит пересечение кривой D – разбиения с не заштрихованной стороны, в заштрихованную (по направлению штриховки), то в этой области число правых корней уменьшается на единицу.

При переходе с заштрихованной стороны на не заштрихованную (против штриховки) число правых корней увеличиваться на единицу. Например, область II на рисунке 2.3б имеет один положительный корень и будет обозначаться D(1), область III имеет 2 положительных корня – D(2).

Методические указания

Для выполнения задания необходимо изучить теоретический материал по учебнику [1, с.155-167] и разобрать пример решения задачи, приведенный в Приложении Е.

Задачу выполняют в следующем порядке:

1)выписывают характеристическое уравнение системы автоматического регулирования;

2)определив варьируемый параметр ν, представляют характеристическое уравнение в виде (8);

3) записывают уравнение границы D-разбиения (9);

4) определяют выражение для варьируемого параметра и выделяют в нем вещественную и мнимую часть (10);

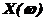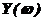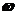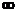5) вычисляют вещественную и мнимую части параметра ν, изменяя от - до + 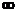и результаты заносят в таблицу;

6) на комплексной плоскости строят границу D-разбиения;

7) штрихуют границу D-разбиения по приведенному выше правилу;

8) определяют область с наибольшим числом левых корней, которая является претендентом на область устойчивости;

9) задаются любым вещественным значением параметра ν из области претендента, подставляют его в характеристическое уравнение и, пользуясь любым критерием устойчивости, проверяют, все ли корни характеристического уравнения при этом будут левыми;

10) если при выбранном ν система будет устойчивой, то область – претендент является областью устойчивости и ее обозначают D(0);

11) если при этом не все корни характеристического уравнения левые, то система автоматического регулирования не имеет области устойчивости;

12) определяют индексы других областей плоскости ν.

Библиографический список

1 Теория автоматического управления: учеб. для вузов [Текст] / С.Е.Душин, Н.С.Зотов и др.; под ред. В.Б.Яковлева. – М: Высш. шк., 2003. – 567 с.: ил.

2 Ким, Д.П. Теория автоматического управления [Текст]: в 2 томах.

Т.1 Линейные системы / Д.П.Ким – М.:ФИЗМАТЛИТ, 2003. – 288 с.

3 Ким, Д.П.Сборник задач по теории автоматического управления. Линейные системы [Текст] / Д.П.Ким, Н.Д. Дмитриева. – М.: ФИЗМАТЛИТ, 2007. – 168 с.

3 Певзнер, Л.Д. Практикум по теории автоматического управления: учеб. пособие [Текст]/ Л.Д.Певзнер. – М.:Высш. шк., 2006. – 590 с.: ил.

5 Филипс, Ч. Системы управления с обратной связью [Текст] / Ч. Филипс, Р Харбор. – М.: Лаборатория Базовых Знаний, 2001. – 616 с.

6 Пантелеев, А.В. Теория управления в примерах и задачах: учеб. пособие [Текст] / А.В.Пантелеев, А.С.Бортаковский. – М.: Высш. шк., 2003. – 583 с.

7 Чмых, Г.И. Теория автоматического управления: сборник задач для практических занятий и самостоятельной работы студентов специальности 220301 всех форм обучения. Ч.1 /Г.И.Чмых. – Красноярск: СибГТУ, 2007. – 60 с.

8 Чмых, Г.И. Теория автоматического управления /Ч.2: сборник задач для практических занятий и самостоятельной работы студентов специальности 220301 очной, заочной, заочной сокращенной форм обучения / Г.И.Чмых. – Красноярск: СибГТУ, 2009. – 48 с.

9 ГОСТ 2.105.-95. Общие требования к текстовым документам [Текст] – Взамен ГОСТ 2.105.-79, ГОСТ 2.906-71; введ. 01-07-96. – М.: Изд-во стандартов, 2002. – С.57-85. – (Единая система конструкторской документации)

10 ГОСТ 2.301-68. Форматы [Текст]. – Взамен ГОСТ 3450-60; введ. 01-01-71. М.: Изд-во стандартов, 1984. – С.3-4. – (Единая система конструкторской документации).

Приложение А

(обязательное)

Ключевые слова