Частное и общее решение. Частный и общий интеграл. Задачи Коши.

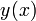Частным решением дифференциального уравнения на интервале называется каждая функция , которая при подстановке в уравнение вида

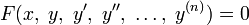
обращает его в верное тождество на интервале .

Зная общее решение однородного дифференциального уравнения и любое частное решение неоднородного уравнения, можно получить общее решение неоднородного уравнения в виде суммы общего решения однородного уравнения и частного решения неоднородного.

Общее решение дифференциального уравнения — функция наиболее общего вида, которая при подстановке вдифференциальное уравнение

вида

обращает его в тождество.

Если каждое решение дифференциального уравнения представимо в виде:

где 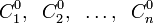— конкретные числа, то функция вида

при всех допустимых значениях параметров (неопределённых констант) называется общим решением дифференциального уравнения.

Пусть 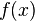определена на . Разобьём на части с несколькими произвольными точками Тогда говорят, что произведено разбиение отрезка Далее выберем произв. точку , ,

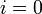Определённым интегралом от функции 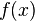на отрезке называется предел интегральных сумм при стремлении ранга разбиения к нулю , если он существует независимо от разбиения и выбора точек , т.е.

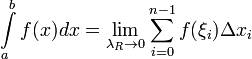
Если существует указанный предел, то функция 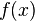называется интегрируемой на по Риману.

Общим интегралом дифференциального уравнения называется общее решение этого уравнения записанное в неявном виде:

Ф(x,y,c)=0

Частным интегралом дифференциального уравненияназывается частное решение уравнения записываемое в неявном виде:

Ф(x,y,c₀ )=0.

Дифференциальное уравнение с разделенными переменными и его решение.

Рассмотрим дифференциальное уравнение вида:

f1(x)dx=f2(y)dy, (1)

которое называется уравнением с разделенными переменными.

Пусть найдено некоторое его решение y(x). При подстановке y=y(x) в дифференциальное уравнение (1) оно обратится в тождество и, интегрируя его, имеем

∫f1(x)dx=∫f2(y)dy+C, (2)

где C - произвольная постоянная. Получили уравнение (2), которому удовлетворяют решения дифференциального уравнения (1). Обратно, каждое решение y(x) уравнения (2) является и решением исходного дифференциального уравнения (1), так как если y(x) обращает в тождество уравнение (2), то, дифференцируя это тождество, получим, что y(x) обращает в тождество и уравнение (1). Следовательно, равенство (2) содержит все решения дифференциального уравнения (1) и оно называется общим интегралом уравнения (1). Из него при определенных условиях можно выразить y от x или x от y.

Если надо выделить частное решение, удовлетворяющее условиям: y=y0 при x=x0, то таким решением является равенство

∫xx0f1(t)dt=∫yy0f2(t)dt,

так как оно содержится в общем интеграле (2) и удовлетворяет начальным условиям.