Свойства дробно-линейной функции

1) Обратная функция также дробно-линейна.

2) Сложная функция, составленная из дробно-линейных, дробно-линейна.

3) Осуществляет однолистное конформное отображение полной z-плоскости на полную w-плоскость.

4) Преобразует любую окружность полной z-плоскости на окружность полной w-плоскости (прямая считается частным случаем окружности – с бесконечным радиусом и с центром, удаленным на бесконечность).

5) Любую пару точек, симметричную относительно окружности C, преобразует в пару точек, симметричных относительно образа окружности C. (Симметричными относительно окружности считаются точки, лежащие на одном луче, проведенном из центра окружности, если произведение расстояний от этих точек до центра равно квадрату радиуса окружности.)

6) Существует одно и только одно дробно-линейное преобразование полной z-плоскости на полную w-плоскость, переводящее три произвольные различные точки в три произвольные различные точки .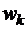

7) Любой круг полной плоскости z с помощью дробно-линейной функции можно преобразовать в любой круг плоскости w.

Рассмотрим в качестве примера отображение верхней полуплоскости на круг (рис. 1.12).

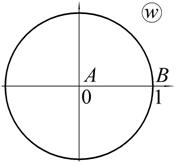
Рис. 1.12.Отображение верхней полуплоскости на круг

Допустим, точка A (z=z₀) переходит в 0, а точка B (z=0) – в 1. Согласно свойству 5 дробно-линейных функций, симметричная относительно действительной прямой точка C ( 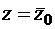) переходит в точку, симметричную точке w=0 относительно окружности, т.е. в точку w=¥. Тогда эти условия можно свести в таблицу

Точка	z	w	Формула
A	z0
C		¥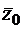
B			,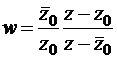

Поскольку точка A (z=z₀) переходит в 0, то числитель дробно-линейной функции можно записать в виде 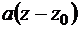. Но тогда , что позволяет положить 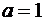. (Поскольку запись выражения для дробно-линейной функции содержит четыре коэффициента, хотя определяется тремя). Далее, так как точка C (z=0) переходит в ¥, то знаменатель примет вид 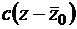. Из третьего условия ( 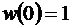) найдем .

В качестве другого примера рассмотрим отображение верхней полуплоскости на верхнюю полуплоскость с соответствием точек, указанным на рис. 1.13.

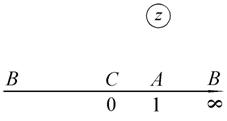
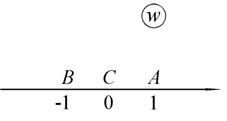
Рис. 1.13.Отображение верхней полуплоскости на верхнюю полуплоскость

Сведем условия в таблицу

Точка	z	w	Формула
C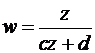
B	¥	-1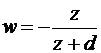
A			,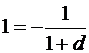

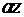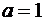Поскольку точка C (z=) переходит в 0, то числитель дробно-линейной функции можно записать в виде . Но тогда , тогда положим . Далее, так как точка B (z=¥) переходит в -1, а предел дробно-линейной функции равен 1/c, то c=1. Из третьего условия (точка A) найдем .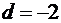

В качестве третьего примера рассмотрим отображение верхней половины единичного круга на первый квадрант с соответствием точек, указанным на рис. 1.14.

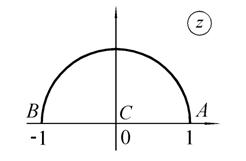
Рис. 1.14.Отображение верхнего полукруга на первый квадрант

Отметим, что при отображении дуга окружности переходит в луч, углы A и C сохраняются, угол B меняет знак. Это позволяет применить для отображения дробно-линейную функцию.

Составим таблицу

Точка	z	w	Формула
A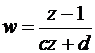
B	-1	¥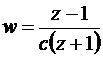
C		i	,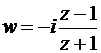

Коэффициенты определяются так же, как и в рассмотренных выше примерах.

Отметим, что в верхнюю полуплоскость первый квадрант можно преобразовать функцией w², а в единичную горизонтальную полосу ABB¢CA¢ функцией 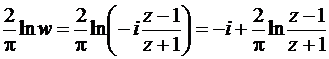(так как логарифм отображает внутренность угла в полосу).