Число-импульсный дв сигнал, последовательный и параллельный двоичный сигналы. (2)
Последовательные двоичные сигналы хорошо использовать при передаче данных на большие расстояния, когда прокладывать многожильный кабель для параллельного двоичного сигнала становится достаточно дорого, ведь в отличие от последовательного параллельный сигнал передается одновременно по нескольким линиям, как это показано на рис.1.3. В приведенном примере параллельного сигнала совокупность нулей и единиц во время первого тактового импульса соответствует числу 3, а во втором, – 10.
Обычно передача цифровых данных на расстояние до нескольких метров производится с помощью параллельных сигналов, а на большие расстояния, – с помощью последовательных сигналов.
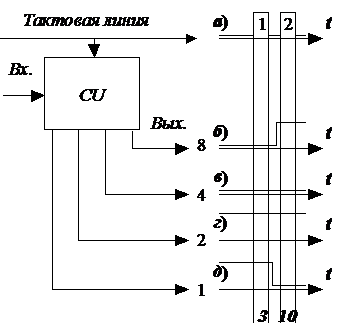
Рис.1.3. Пример параллельного двоичного сигнала, поступающего одновременно с нескольких выводов цифрового устройства CU, в котором:
а)– сигнал передаваемый по тактовой линии;
б) – сигнал, поступающий с старшего выхода цифрового устройства CU, которому соответствует весовой коэффициент 8;
в) – сигнал, поступающий с среднего выхода цифрового устройства CU, которому соответствует весовой коэффициент 4;
г) – сигнал, поступающий с среднего выхода цифрового устройства CU, которому соответствует весовой коэффициент 2;
д) – сигнал, поступающий с младшего выхода цифрового устройства CU, которому соответствует весовой коэффициент 1.
Как видно из трех вышеприведенных рисунков, самым быстрым способом передачи информации является использование параллельного сигнала, но при этом требуются самые большие аппаратные затраты.
Самым медленным, но зато и самым простым и требующим самые малые затраты оборудования, является применение число–импульсного сигнала. Последовательный позиционный двоичный сигнал является промежуточным между параллельным и число–импульсным сигналами.
Билет12
2) Параметры цифровых микросхем делятся на три группы: статические, динамические и интегральные.
Статические параметры цифровых микросхем характеризуют микросхему в статическом (установившемся) режиме. К ним относятся:
а) напряжение источника питания Uпит. [В] и допуск на его изменение DUпит. (для ТТЛ DUпит. = ± 5; 10 %; для большинства же серий КМОП допустимо питание в пределах от 3 до 15 В);
б) входные и выходные допустимые напряжения U0вх.max, U0вых.max, U1вх.min, U1вых.min [В];
в) входные и выходные токи при лог.0 и лог.1 и их допуски: I0вх.max, I0вых.max, I1вх.min, I1вых.min;
г) коэффициент разветвления по выходу Кразв.=10 (это число входов микросхемы данной серии, которые допустимо подключать к данному выходу микросхемы );
д) коэффициент объединения по входу Коб. (обычно это число входов данной микросхемы ). Как правило Коб. = 2; 3; 4 и 8. Если нужно другое число, то применяют специальные микросхемы , – расширители, или собирают схему по законам булевой алгебры;
е) потребляемая мощность (статическая) обычно рассматривается как полусумма мощностей, потребляемых при нуле и при единице:
РПОТ = (Р0ПОТ + Р1ПОТ) / 2 ;
ж) помехоустойчивость (статическая) Uпом. – допустимое напряжение помех на входе микросхемы , определяется из двух значений:
| U1ВЫХ.MIN – U1ВХ.MAX | = U1ПОМ , или | U0ВЫХ.MAX – U0ВХ.MIN| = U0ПОМ.
Из этих двух значений выбирается меньшее. Эти значения помехоустойчивости даны для предельных значений питающих напряжений, температуры окружающей среды и др. условий. Реальная помехоустойчивость примерно в два раза лучше. В зависимости от продолжительности помехи различают статическую и динамическую помехоустойчивость. Статическую помехоустойчивость связывают с помехами, длительность которых больше времени переходных процессов, а динамическую, – с кратковременными помехами. Динамическая помехоустойчивость также выше за счет того, что от короткого импульса помех микросхемы просто не успевает переключиться.
Динамические параметры цифровых микросхем определяют максимальную частоту смены входных состояний, при которой не нарушается нормальное функционирование микросхем. Способы определения временных динамических параметров показаны на рис. 5.2.2.
К динамическим параметрам цифровых интегральных микросхем обычно относят следующие:
а) tзд.р. – среднее время задержки распространения переднего и заднего фронтов:
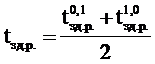
б) t0,1Ф длительность фронта выходного сигнала при перепаде от нуля к единице (от 0.1 до 0.9 амплитуды сигнала) и t1,0Ф длительность фронта выходного сигнала при перепаде от 1 к 0 (от 0.9 до 0.1 амплитуды сигнала);
в) максимальная частота переключения fMAX £ (t0,1Ф + t1,0Ф) / 2.
Интегральные параметры цифровых микросхем отражают уровень развития технологии и схемотехники, а также качество цифровых микросхем:
а) энергия переключения ЭПЕР = РПОТР.СР × tЗД.Р [пДж];
б) степень интеграции N = lg n, где n, – число простых логических элементов (2И–НЕ) на кристалле (при N = 2 микросхемы обычно называют схемами средней интеграции, – СИС; при N = 3 микросхемы обычно называют схемами большой интеграции, – БИС; при N = 4 микросхемы обычно называют схемами сверх большой интеграции, – СБИС).
Билет13
1)Минимизация булевых выражений по картам Карно. (1
Основой минимизации алгебраическим способом является последовательное использование законов булевой алгебры и правил преобразований. Карта Карно изображает в виде графических квадратов (клеток) все возможные комбинации переменных, причем переменные, определяющие координаты клеток карты, размещают так, чтобы при переходе из одной клетки в соседнюю, как по горизонтали, так и по вертикали, изменялась только одна переменная.
Если требуется получить карту Карно для какой–либо функции, сначала надо записать эту функцию в СДНФ, – в совершенной дизъюнктивно нормальной форме, или в виде таблицы истинности.
Каждое слагаемое булева выражения в СДНФ, или каждая единица в столбце функции таблицы истинности, задается на карте Карно единицей в соответствующей клетке. Координаты этой клетки содержат те же входные переменные и их инверсии, что и данное слагаемое СДНФ булева выражения ( или данная строка таблицы истинности ).
Таблица истинности для четырех переменных включает 16 строк, следовательно карта Карно должна состоять из 16 клеток, как показано на рис.4.10.1.
`А`В `А В А В А`В
 |
`С`D 1 1
 |
`C D 1 1
 |
C D 1 1
 |
C`D

Рис.4.10.1. Пример карты Карно для 4–х переменных.
У карты Карно для четырех переменных клетки крайнего левого столбца должны рассматриваться как соседние для клеток крайнего правого столбца, а клетки верхней строки, – как соседние для клеток нижней строки. Другими словами можно сказать, что эта карта расположена на поверхности цилиндра (склеили правый край карты с левым ), изогнутого и растянутого так, что его верхний срез соединяется с нижним срезом; при этом цилиндр превращается в тор (бублик).
Правила упрощения заполненной карты Карно для четырех переменных заключаются в следующем :
– соседние две, четыре, или восемь единиц обводят общим контуром;
– контур должен быть прямоугольным без изгибов или наклонов;
– каждый контур превращает все входящие в него единицы в одну, т.е. объединенные таким образом слагаемые СДНФ булева выражения дают одно слагаемое в упрощенном выражении;
– те входные переменные, которые входят в координаты данного контура совместно со своими инверсиями, исключаются из слагаемого, которое дает этот контур в упрощенное выражение.
Примеры упрощения булевых выражений с помощью карты Карно:
1. F1 = `А В`С`D1 + A B`C`D2 +`A B`C D3 + A B`C D4 +
+ `A`B C`D5 + `A B C`D6 .
`А`В `А В А В А`В
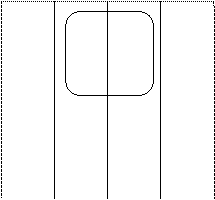 |
 `С`D 11 12 B`C
`С`D 11 12 B`C
 |
 `C D 13 14 `A C`D
`C D 13 14 `A C`D
 |
C D
 |
 C`D 15 16
C`D 15 16
 F1 = B C + `A C`D
F1 = B C + `A C`D
Рис.4.10.2. Пример минимизации булевой функции F1 с помощью карты Карно для 4–х переменных.
В первом примере минимизации булевой функции F1 нижний контур из двух единиц 15 и 16 , соответствующие пятому и шестому слагаемым в исходном булевом выражении, дает возможность опустить B и`B. После этого в нем остается произведение `A C`D. В верхнем контуре из четырех единиц 11, 12, 13 и 14 , соответствующие первым четырем слагаемым в исходном булевом выражении попарно опускаются A и`A, D и`D, так что в результате этого верхний контур дает произведение B C.
2.F2 =`А`В`С`D1 +`A B`C`D2 + A B`C`D3 +`A`B C`D4 +`AB C`D5
`А`В `А В А В А`В
 |
 `С`D 11 12 13 B`C`D
`С`D 11 12 13 B`C`D
 |
 `C D `A`D
`C D `A`D
 |
C D
 |
C`D 14 15


 F2 =`A`D + B`C`D
F2 =`A`D + B`C`D
Рис.4.10.3. Пример минимизации булевой функции F2 с помощью карты Карно для 4–х переменных.
Во втором примере минимизации булевой функции F2 контур из двух единиц 12 и 13 , соответствующие второму и третьему слагаемым в исходном булевом выражении, дает возможность опустить А и`А. После этого в нем остается произведение B`C`D. В контуре из четырех единиц 11, 12, 14 и 15 , соответствующие другим четырем слагаемым из исходного булева выражения, попарно опускаются В и`В, С и`С, так что в результате этого верхний контур дает произведение `A`D. Карта Карно представляется в данном случае свернутой в цилиндр, в котором верхний край совмещается с нижним.
Этот пример показывает также, что контуры могут накладываться друг на друга.
Билет13
3) 2) Умножение столбиком
0 1 1 0 =5
0 1 0 1 =6
0 1 1 0
0 0 0 0
0 1 1 0
0 1 1 1 1 0 30
Деление
Помещаем делитель под делимым как можно левее, производим вычитание из делимого, после вычитания в наиболее значимый разряд частного заносится 1, если вычитание невозможно из-за того что остаток оказывается отриц вычитание не выполняется и в наиб значимый разря частного заносится 0. затем сдвигаем весь делитель на одну позицию вправо и втом же духе.
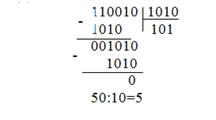

Делимое больше делителя Делимое меньше делителя
Билет14
1)Различия между непрерывным и двоичным (цифровым) сигналами. Последовательные и параллельные двоичные сигналы. (1
Сигналы можно разделить на две класса:
– аналоговые, непрерывные, изменяющиеся плавно;
– дискретные, изменяющиеся скачками обычно в определенные моменты времени.
Множество допустимых уровней дискретного сигнала может быть любым, однако есть один самый распространенный тип дискретного сигнала, у которого возможны только два значения: ВЫСОКИЙ (HIGH, 1) и НИЗКИЙ (LOW, 0) уровни. Такой сигнал называют двоичным, а зачастую цифровым (строго говоря, цифровой сигнал может иметь не только два уровня).
Двоичные (цифровые) сигналы можно подразделить на число–импульсные, последовательные и параллельные позиционные сигналы.
Самыми простыми двоичными сигналами являются число–импульсные сигналы, у которых информационным параметром является количество импульсов N за время заданного постоянного интервала времени, или за время между двумя определенными метками времени, причем ни длительность импульсов, ни их расположение при этом не имеют значения. На рис.2.1.1 показан пример число–импульсного двоичного сигнала, в котором отметками начала и конца интервалов, в которых производят подсчет числа импульсов сигнала, служат достаточно длительные паузы между пачками импульсов. Такой вид может иметь сигнал набора номера в телефонных аппаратах с импульсным набором, которые распространены в нашей стране.
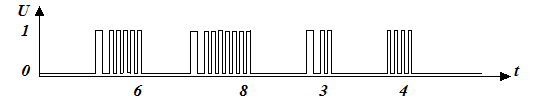
Рис. 2.1.1. Пример число–импульсного двоичного сигнала, содержащего 6, 8, 3 и 4 импульса соответственно в первой, второй, третьей и четвертой посылках.
Число–импульсные сигналы настолько просты, что как правило, когда говорят о двоичных или цифровых сигналах, то подразумевают при этом один из двух позиционных видов двоичного сигнала, – последовательный, или параллельный двоичный сигнал, для которых уже имеет значение и длительность и положение каждого единичного импульса.
В последовательном двоичном сигнале информация заключена во временной последовательности появления нулей и единиц внутри своей группы, приходящейся на определенное число тактов дискретного времени. В каждой такой группе первая позиция обычно соответствует самому младшему разряду, имеет самый малый вес, а все последующие позиции (номера дискретного времени внутри группы) имеют последовательно нарастающие веса вплоть до последней позиции с максимальным весом, соответствующей старшему разряду. Поскольку в двоичном сигнале имеется только два допустимых значения, то все веса, разряды кода являются степенями двойки.
На рис. 2.1.2 показан пример последовательного двоичного сигнала, поступающего с одного вывода какого–то цифрового устройства CU. На этом рисунке, кроме сигналов по тактовой линии и самого последовательного двоичного сигнала, показано также цифровое устройство CU с его входами и выходом. Под каждым тактовым отрезком времени приведены их весовые коэффициенты.
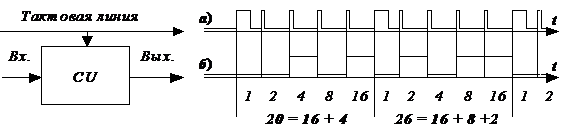
Рис. 2.1.2. Пример последовательного двоичного сигнала, поступающего с одного вывода цифрового устройства CU, где:а)– сигнал передаваемый по тактовой линии;
б) – последовательность нулей и единиц, в первом интервале соответствующая числу 20, а во втором, – 26.
