Простейшие фигуры в пространстве, как они обозначаются

Простейшие фигуры в пространстве: точка, прямая, плоскость. На рисунках плоскости изображаются в виде параллелограмма или в виде произвольной области и обозначаются греческими буквами α, β, γ и т.д. Точки А и В лежат в плоскости β (плоскость β проходит через эти точки), а точки M, N, P не лежат в этой плоскости. Коротко это записывают так: А ∈ β, B ∈ β,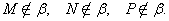

Взаимное расположение прямых в пространстве

Возможны четыре различных случая расположения двух прямых в пространстве:

– прямые скрещивающиеся, т.е. не лежат в одной плоскости;

– прямые пересекаются, т.е. лежат в одной плоскости и имеют одну общую точку;

– прямые параллельные, т.е. лежат в одной плоскости и не пересекаются;

– прямые совпадают.

Взаимное расположение прямой и полоскости

Известны три варианта взаимного расположения прямой и плоскости:

1. Прямая принадлежит плоскости.
2. Прямая параллельна плоскости.
3. Прямая пересекает плоскость.

Признак праллельности 2-х полоскостей

Если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости , то эти плоскости параллельны.

Признак перпендикулярности прямой и плоскости

Если прямая, пересекающая плоскость, перпендикулярна двум прямым в этой плоскости, проходящим через точку пересечения данной прямой и плоскости, то она перпендикулярна плоскости.

Признак перпендикулярности прямой и плосткости

Если прямая, пересекающая плоскость, перпендикулярна двум прямым в этой плоскости, проходящим через точку пересечения данной прямой и плоскости, то она перпендикулярна плоскости.

Теорема о трех перпендикулярах

Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна наклонной.
И обратно: Если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.

Двугранный угол

Двугранный угол — пространственная геометрическая фигура, образованная двумя полуплоскостями, исходящими из одной прямой, а также часть пространства, ограниченная этими полуплоскостями.

Мера двугранного угла

Градусной мерой двугранного угла называется градусная мера его линейного угла.

Признак перпендикулярности двух плоскостей

Если плоскость проходит через прямую перпендикулярную другой плоскости, то эти плоскости перпендикулярны.

Перпендикуляр и наклонная

Перпендикуляром, опущенным из данной точки данную плоскость, называется отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, перпендикулярной плоскости. Конец этого отрезка, лежащий в плоскости, называется основанием перпендикуляра.
Наклонной, проведенной из данной точки к данной плоскости, называется любой отрезок, соединяющий данную точку с точкой плоскости, не являющийся перпендикуляром к плоскости.

Угол между прямой плоскостью

Угол между прямой и плоскостью — это угол между прямой и ее проекцией на данную плоскость.

Угол между полоскотями

Угол между двумя пересекающимися плоскостями равен углу между прямыми, по которым они пересекаются с любой плоскостью, перпендикулярной их линии пересечения.

Основные свойства параллельного проектирования

Свойство 1. Если прямая параллельна или совпадает с прямой l, то ее проекцией в направлении этой прямой является точка. Если прямая не параллельна и не совпадает с прямой l, то ее проекцией является прямая.

Свойство 2. Проекция отрезка при параллельном проектировании есть точка или отрезок, в зависимости от того лежит он на прямой, параллельной или совпадающей с прямой l, или нет. Параллельное проектирование сохраняет отношение длин отрезков, лежащих на прямой, не параллельной и не совпадающей с прямой l. В частности, при параллельном проектировании середина отрезка переходит в середину соответствующего отрезка.

Свойство 3. Если две параллельные прямые не параллельны прямой l, то их проекции в направлении l могут быть или параллельными прямыми или одной прямой.

Основные виды чисел

Натуральные числа – это числа, получаемые при естественном счёте предметов, а вернее при их нумерации («первый», «второй», «третий»...). Множество натуральных чисел обозначается латинской буквой N (можно запомнить, опираясь на английское слово natural). Можно сказать, что N ={1,2,3,....}

Целые числа – это числа из множества {0, 1, -1, 2, -2, ....}. Это множество состоит из трех частей – натуральные числа, отрицательные целые числа (противоположные натуральным числам) и число 0 (нуль). Целые числа обозначаются латинской буквой Z. Можно сказать, чтоZ={1,2,3,....}.

Рациональные числа – это числа, представимые в виде дроби 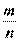, где m — целое число, а n — натуральное число. Для обозначения рациональных чисел используется латинская буква Q. Все натуральные и целые числа – рациональные. Также в качестве примеров рациональных чисел можно привести: , , .

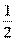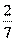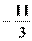Действительные (вещественные) числа – это числа, которое применяются для измерения непрерывных величин. Множество действительных чисел обозначается латинской буквой R.

Абсолютная погрешность

Под абсолютной погрешностью измерения понимают разность между полученным в ходе измерения и истинным значением физической величины:

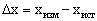
Относительная прогрешность

Относительная погрешностьпредставляет собой отно­шение абсолютной погрешности к истинному значению измеряемой величины:

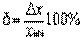
Округление чисел

Под округлением понимают отбрасывание одной или нескольких последних цифр в десятичном представлении числа. Если первая из отбрасываемых цифр больше 5, то последняя из сохраняющихся цифр увеличивается на 1. Если первая из отбрасываемых цифр равна 5, а за ней следуют одна или несколько значащих цифр, то последняя из сохраняющихся цифр также увеличивается на 1.