Арифметические векторные пространства

Определение 1: n-мерным вектором над полем F называется кортеж из n элементов (упорядоченная 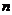-ка чисел) поля F. Множество всех n – мерных векторов над полем F обозначается символом Fⁿ.

Векторы обычно записываются в виде строки или столбца (показать оба вида).

На множестве n–мерных векторов над полем F введем отношение равенства, операцию сложения векторов и операцию умножения вектора на скаляр.

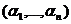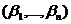Определение 2: Векторы и называются равными, если .

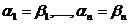Определение 3: Сумма векторов 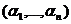и 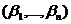называется вектор ; + = .

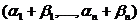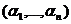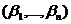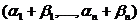Определение 4: Произведением скаляра 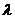на вектор 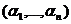называется вектор 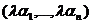, т.е. 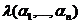= 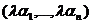. Операцию умножения на скаляр 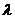обозначим символом 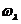, т.е. = .

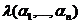Для каждого 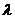из F 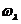есть унарная операция на множестве n- мерных векторов Fⁿ.

Вектор (0,…,0) называется нулевым вектором и обозначается символом 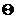. Нулевой вектор является нейтральным элементом относительно сложения.

Вектор 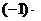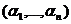называется вектором, противоположным вектору 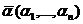, и обозначается символом 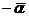. Очевидно, .

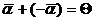Определение 5: Арифметическим n–мерным пространством над полем F называется множество Fⁿ c заданными на нем бинарной операцией сложения и унарными операциями 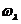, т.е. алгебра .

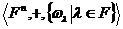Теорема 1:Операции векторного пространства Fⁿ обладают следующими свойствами:

1. Алгебра 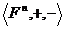, где 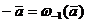для любого 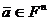, есть абелевая группа;

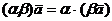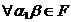2. Умножение на скаляры ассоциативно, т.е. для и ;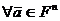

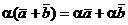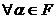3. Умножение на скаляр дистрибутивно относительно сложения, т.е. для и ;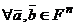

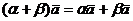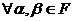4. Умножение на скаляр дистрибутивно относительно сложения скаляров; т.е. для и ;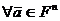

5. 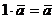для любого 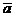из Fⁿ.

Пусть F – поле скаляров и V = Fⁿ n–мерное арифметическое пространство над F 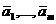- произвольная система векторов пространства V.

Определение 6: Линейной комбинацией системы векторов 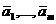называется вектор вида 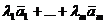, где 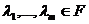. Скаляры 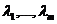называются коэффициентами линейной комбинации. Линейная комбинация называется нетривиальной, если хотя бы один ее коэффициент отличен от нуля. Линейная комбинация называется тривиальной, если все ее коэффициенты равны нулю.

Определение 7: Система векторов 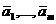называется линейно независимой, если для любых скаляров 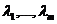из равенства 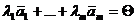следуют равенства 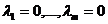. Пустая система векторов считается линейно независимой.

Другими словами, конечная система векторов линейно независима в том и только в том случае, когда всякая нетривиальная линейная комбинация векторов системы не равна нулевому вектору.

Определение 8: Система векторов 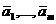называется линейно зависимой, если существуют скаляры 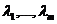, не все равные нулю, такие, что .

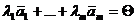Другими словами, конечная система векторов называется линейно зависимой, если существует нетривиальная линейная комбинация векторов системы равная нулевому вектору.

Система векторов 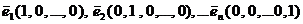называется системой единичных векторов векторного пространства Fⁿ. Эта система векторов линейно независима. В самом деле, для любых скаляров 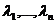из равенства 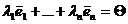следует равенство 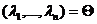и, значит, равенства .

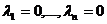Рассмотрим свойства линейной зависимости и независимости системы векторов.

1. Система векторов, содержащая нулевой вектор, линейно зависима.

Доказательство: Если в системе векторов 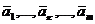один из векторов, например вектор 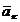нулевой, то линейная комбинация векторов системы, все коэффициенты которой нулевые, за исключением коэффициента при 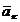, равна нулевому вектору. Следовательно, такая система векторов линейно зависима.

2. Система векторов линейно зависима, если какая – нибудь ее подсистема линейно зависима.

Доказательство: Пусть 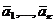- линейно зависимая подсистема системы 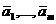, т.е. 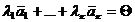, причем хотя бы один из коэффициентов 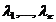отличен от нуля. Тогда 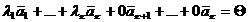. Следовательно, система векторов 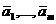линейно зависима.

3. Система векторов

(1) ,

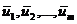в которой 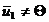линейно зависима тогда и только тогда, когда хотя бы один из векторов 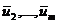является линейной комбинацией предшествующих векторов.

Доказательство: Пусть система (1) линейно зависима и 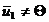. Тогда существуют скаляры 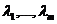, не все равные нулю, такие, что

(2) .

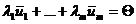Обозначим через 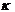наибольшее из чисел 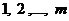удовлетворяющее условию 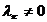. Тогда равенство (2) можно записать в виде

(3) .

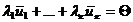Отметим, что 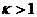, ибо в противном случае 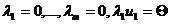, следовательно, 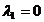, поскольку 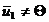. Из (3) следует равенство

.

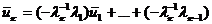Предположим теперь, что вектор 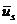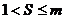, есть линейная комбинация 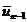предшествующих ему векторов, т.е. 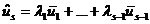. Тогда 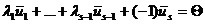т.е. подсистема 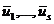системы линейно зависима. Следовательно, по св. 2. линейно зависима и исходная система (1).

4. Если система векторов 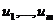( 1 ) линейно независима, а система векторов

(2) 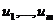, 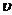линейно зависима, то вектор 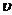линейно выражается через векторы

(1) 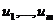и притом единственным образом.

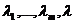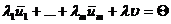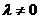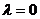
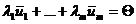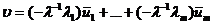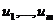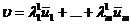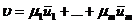Доказательство: По условию система (2) линейно зависима, т.е. существуют скаляры , не все равные нулю, такие, что (3) . При этом , так как при , что противоречит линейной зависимости системы(1). Из (3) следует равенство . И мы получим, что v линейно выражается через . Если предположим, что существуют два таких представления и , то

.

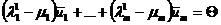В силу линейной независимости (1) отсюда следует, что 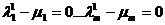и .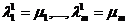

5. Пусть S¹ – какая–либо часть (подсистема) системы S. Подсистема S¹ называется базисом системы S, если S¹ –максимальная линейно независимая подсистема.

Иными словами, подсистема S¹ есть базис системы S, если:

1. она линейно независима;

2. добавление к подсистеме S¹ любого другого вектора из системы S превращает эту подсистему в линейно зависимую.

С каждой системой векторов можно связать некоторое число – ранг системы, являющийся одной из важнейших характеристик системы.

Рангом системы векторов называется число векторов в любом базисе системы векторов.

Другими словами, ранг системы векторов – это максимальное число линейно независимых векторов в данной системе.