Схема однородных независимых испытаний
Теория вероятности
Комбинаторика
Соединения:
1. Перестановка: Pn=n!
2. Сочетания: 

3. Размещения: 
Свойства сочетаний:
1. 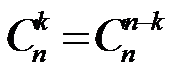
2. 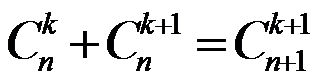
3. 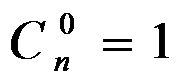
4. 0! = 1; 1!=1.
Сумма событийА и В– такое событие С, которое состоит в появлении или А, или В, или и А, и В одновременно: А+В=С=А 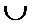 В.
В.
Произведение событийА и В – такое событие С, которое состоит в том, что появляется и А, и В одновременно.
Законы:
1. (А+В)*С=АС+ВС – ассоциативный закон.
2. А*В=В*А; А+В=В+А – коммутативный закон.
События Аj составляют полную группу событий, если они попарно несовместны и в опыте одно из них обязательно произойдет:
1) Аi*Aj=Ø  i, j
i, j
2) A1+A2+…+An= 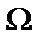
Относительная частота события:
W(A)=m/n
Классическое определение вероятности:
P(A)= W(A)=m/n
События равновозможные, если в условиях опыта ни одно из этих событий не является более вероятным, чем др.
Единовозможные события – события, кроме которых не могут произойти никакие др.
Геометрическое определение вероятности:
P(g)=mesg/mesG
Аксиомы ТВ:
1. Р(А)  0
0
2. P(  )=1
)=1
3. P(Ø)=0
4. P(A+B)=P(A)+P(B), А, В – несовместные.
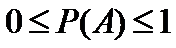
Зависимые событияА и В – это события, вероятность одного из которых меняется в зависимости от того, произошло др. событие или нет, в противоположном случае они независимы.
Условной вероятностьюназывается вероятность события В при условии, что событие А наступило:
PA(B)=P(AB)/P(A)
Теорема умножения вероятностей:
P(AB)=P(A)*PA(B) – вероятность появления 2-х событий А и В равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что 1-ое событие уже наступило.
P(AB)=P(A)*PA(B)=P(B)*PB(A)
Если А и В независимы Р(АВ)=Р(А)*Р(В).
Если 3 события А, В, С независимы Р(АВС)=Р(А)*Р(В)*Р(С).
Если А, В, С зависимы Р(АВС)=Р(А)*РА(В)*РАВ(С).
Несколько событий называются попарно независимыми, если каждые 2 из них независимы.
Несколько событий независимы в совокупности, если независимы каждые 2 из них и независимы каждое событие и все возможные произведения остальных.
Теорема сложения:
Вероятность появления одного из нескольких попарно независимых событий равна сумме вероятностей этих событий:
P(A1+…+An)= 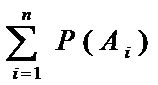 .
.
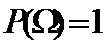
 .
.
Вероятность появления хотя бы одного из п событий  независимых в совокупности равна разности между единицей и произведением вероятности противоположных событий:
независимых в совокупности равна разности между единицей и произведением вероятности противоположных событий:
 .
.
Два события называют совместными, если появление одного из них не исключает появление другого в одном и том же испытании.
Теорема. Вероятность появления хотя бы одного из 2-х совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
Р(А+В)=Р(А)+Р(В)-Р(АВ).
Независимые события:
Р(АВ)=Р(А)*Р(В)
Р(А+В)=Р(А)+Р(В)-Р(А)*Р(В).
Зависимые события:
Р(А+В)=Р(А)+Р(В)-Р(А)*РА(В).
Несовместные события:
А*В=Øи Р(АВ)=0 → Р(А+В)=Р(А)+Р(В).
Формула полной вероятности
Теорема. Вероятность события А, которое может наступить при условии появления одного из несовместных событий В1, В2,…,Вп, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А:
P(A)= 
Формула Байеса
Формула Байеса позволяет переоценить вероятности гипотез после того, как становится известным результат испытания, в котором появилось событие А:
 .
.
Случайные величины
Дискретная СВ – такая величина, которая может принимать значение из конечного или счетного множества изолированных значений.
Непрерывная величина – такая величина, значение которой сплошь заполняет определенный интервал.
 - условие нормировки.
- условие нормировки.
Мода – наивероятнейшее значение СВ:
пр-q≤M0≤np+q.
Медиана (Ме) – величина, которая делит всю совокупность возможных значений на 2 части такие, что Р(Х>Me)=0,5, P(X<Me)=0,5.
Мат.ожидание – среднее значение СВ:
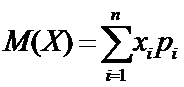 .
.
Дисперсия: 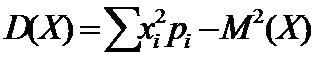 .
.
Среднеквадратическое отклонение (СКО):
 .
.
Правило 3-х сигм:
Р(тх - 3σ<X<mx+3σ)=0,997 – случайное отклонение Х от М(Х), превышающее 3σ, маловероятно.
Начало момента распределения: m1=M(X)=a;
m2=M(X2); m3=M(X3); m4=M(X4).
Центральный момент: 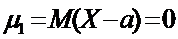 ,
,  ,
, 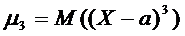 ,
, 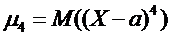 .
.
Свойства мат.ожидания:
1. М(С)=С.
2. М(СХ)=СМ(Х).
3. М(Х+У)=М(Х)+М(У).
4. М(ХУ)=М(Х)М(У).
Следствия из свойств:
1. М(Х-У)=М(Х)-М(У).
2. М(Х-М(Х))=0.
Дискретная СВ:
Дисперсия:
D(X)=M(X-M(X))2;
D(X)=M(X2)-M2(X);
 .
.
Свойства дисперсии:
1. D(C)=0.
2. D(CX)=C2D(X).
3. D(X+Y)=D(X)+D(Y), X, Y – независимые.
4. D(X-Y)=D(X)+D(Y).
СКО: 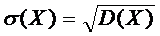 .
.
Коэффициент ковариации: 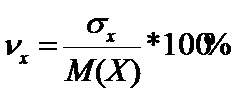 .
.
Смешанный центральный момент:
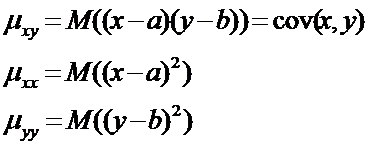
Если Х, У – зависимые, то:

Ассиметрия: 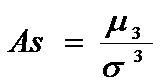 .
.
Эксцесс: 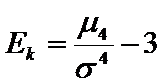 .
.
Функция распределения:
F(x)=P(X<x).
Свойства функции распределения:
1. F(x)  .
.
2. F(x) – неубывающая.
3. F(x) – непрерывна слева.
4. 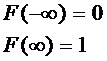 .
.
Мат.ожидание и дисперсия среднеарифметического:
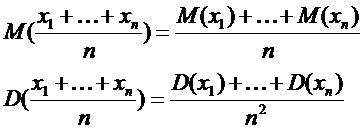 .
.
Непрерывная СВ:
Свойства функции распределения:
1. F(x)  .
.
2. F(x) – неубывающая.
3. P(α<X<β)=F(β) – F(α).
4. P(X=c)=0.
5. Если Х  , то F(X≤a)=0, F(X>b)=1.
, то F(X≤a)=0, F(X>b)=1.
P(α<X<β)=P(α≤X< β)=P(α<X≤ β)=P(α≤X≤ β).
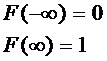 .
.
Плотность распределения:
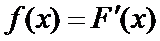 .
.
Свойства:
1. f(x)≥0.
2. Х  , то
, то 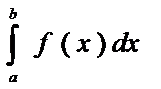 =1.
=1.
3. Х  , то
, то  .
.
4. P(α<X<β)= 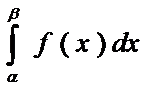 .
.
5. F(x)=  .
.
6. P(α<X<β)= площадь кривой, ограниченной прямыми х= α, х= β, у=0 и у=f(x).
Числовые характеристики НСВ:
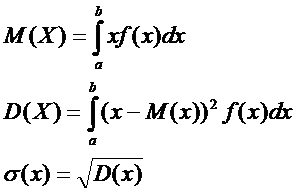
Мода – возможное значение НСВ, которому соответствует максимум ее диф. ф-ции.
Медиана: Р(X<me)=P(X>me).
Начальный момент к-го порядка:
 .
.
Центральный момент к-го порядка:
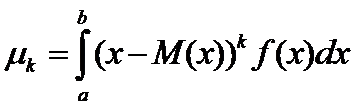 .
.
Вероятность попадания в интервал нормально распределенной СВ Х:
 .
.
Неравенство Чебышева:
 .
.
Теорема Чебышева:
 .
.
Теорема Бернулли:
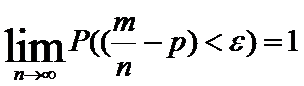 .
.
Характеристики рассеяния.
Дисперсия
Дисперсия (D[x]) характеризует рассеивание или разряженность случайной величины около ее математического ожидания.
Для дискретных 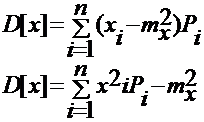
Для непрерывных
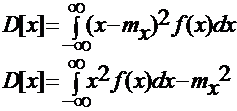
Дисперсия случайной величины всегда величина положительная
Размерность дисперсии равна квадрату разности случайной величины
Биномиальное распределение.
Биномиальным называют законы распределения случайной величины Х числа появления некоторого события в n опытах если вероятность р появления события в каждом опыте постоянна
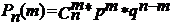
Сумма вероятностей представляют собой бином Ньютона
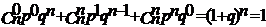
Для определения числовых характеристик в биномиальное распределение подставить вероятность которая определяется по формуле Бернули.
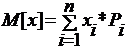
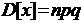
При биномиальном распределении дисперсия равна мат. Ожиданию умноженному на вероятность появления события в отдельном опыте.
Распределение Пуассона
Когда требуется спрогнозировать ожидаемую очередь и разумно сбалансировать число и производительность точек обслуживания и время ожидания в очереди. Пуассоновским называют закон распределения дискретной случайной величины Х числа появления некоторого события в n-независимых опытах если вероятность того, что событие появится ровно m раз определяется по формуле.
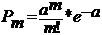 a=np
a=np
n-число проведенных опытов
р-вероятность появления события в каждом опыте
В теории массового обслуживания параметр пуассоновского распределения определяется по формуле
а=λt , где λ - интенсивность потока сообщений t-время
Необходимо отметить, что пуассоновское распределение является предельным случаем биномиального, когда испытаний стремится к бесконечности, а вероятность появления события в каждом опыте стремится к 0.
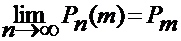
Пуассоновское распределение является единичным распределением для которого такие характеристики как мат. Ожидание и дисперсия совпадают и они равны параметру этого закона распределения а.
Закон равномерной плотности
Равномерным называется распределение непрерывной случайной величины Х все значения которой лежат на отрезке [a;b] и имеют при этом постоянную плотность распределения
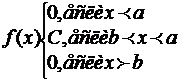
площадь под кривой распределения равна 1 и поэтому с(в-а)=1
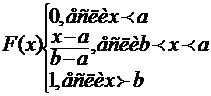
вероятность попадания случайной величины Х на интервал от (α;β)
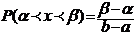
α=а, если α<а
β=в, если β>в
основные числовые характеристики закона распределения плотности вычисляются по общим формулам и они равны
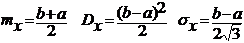
Мат. статистика
Выборочная сумма:
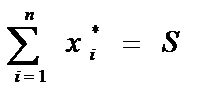 .
.
Выборочное среднее:
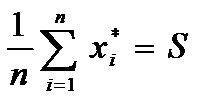 .
.
Выборочная дисперсия:
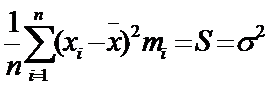 , где тi – частота.
, где тi – частота.
Выборочное СКО:
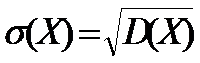 .
.
Эмпирическая функция распределения:
F*(x)=P(X<x)
F*(x)= 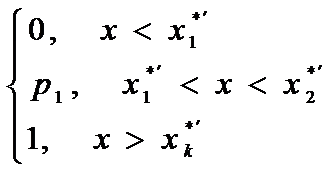 .
.
Точечные оценки:
Несмещенная оценка генеральной средней (мат.ожидания):
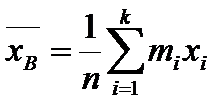 , хi – варианта выборки, mi – частота варианты хi,
, хi – варианта выборки, mi – частота варианты хi, 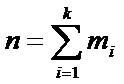 - объем выборки.
- объем выборки.
Смещенная оценка генеральной дисперсии– выборочная дисперсия:
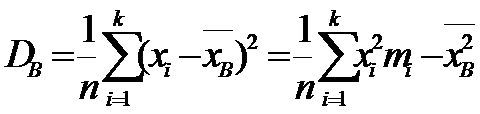 , так как
, так как
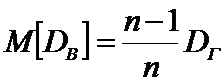 .
.
Несмещенной оценкой генеральной дисперсии служит «исправленная дисперсия»:
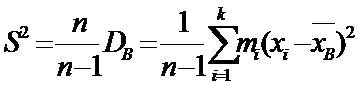 . При п<30.
. При п<30.
Коэффициент вариации:
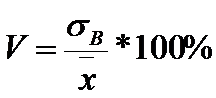 .
.
Центральный момент к-го порядка:
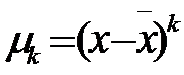 .
.
Начальный момент к-го порядка:
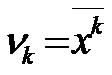 .
.
Ассиметрия: 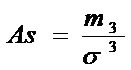 , т3=
, т3= 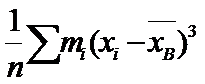
Эксцесс: 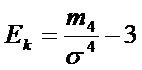 , где т4=
, где т4= 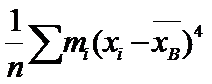
Групповая средняя: 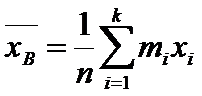 .
.
Общая средняя: 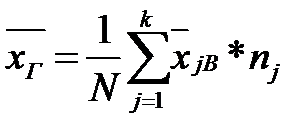 , где
, где 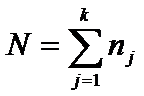 .
.
Общая дисперсия: 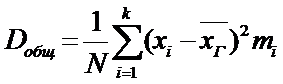 .
.
Интервальные оценки:
Доверительный интервал для мат.ожидания а нормально распределенного количества признака Х :
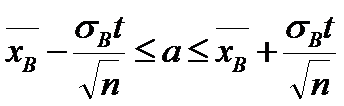 .
.
Критерий согласия Пирсона:
Если число наблюдений очень велико, то закон распределения СВ не зависит от того, какому закону подчинена генеральная совокупность. Он приближается к распределению 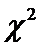 с к степенями свободы, а сам критерий называется критерием согласия Пирсона:
с к степенями свободы, а сам критерий называется критерием согласия Пирсона:
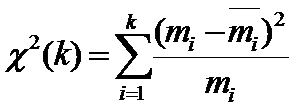 , где к – количество интервалов сгруппированного ряда, тi>0,05n.
, где к – количество интервалов сгруппированного ряда, тi>0,05n.
Количество степеней свободы: r=k-p-1, где к – количество интервалов, р – количество параметров закона.
Уровень значимости α:
α=0,05 и α=0,01.
Если 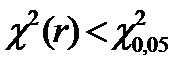 , то Н0 принимается, т.е. предполагаемый закон распределения отвечает эмпирическим данным. При этом мы ошибаемся в 5-ти случаях из 100, принимая возможно ошибочную гипотезу (ошибка 2-го рода).
, то Н0 принимается, т.е. предполагаемый закон распределения отвечает эмпирическим данным. При этом мы ошибаемся в 5-ти случаях из 100, принимая возможно ошибочную гипотезу (ошибка 2-го рода).
Если 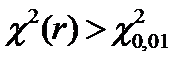 , то Н0 отвергается, т.е. предполагаемый закон не отвечает эмпирическим данным. При этом мы ошибаемся в 1-ом случае из 100, отбрасывая правильную гипотезу (ошибка 1-го рода).
, то Н0 отвергается, т.е. предполагаемый закон не отвечает эмпирическим данным. При этом мы ошибаемся в 1-ом случае из 100, отбрасывая правильную гипотезу (ошибка 1-го рода).
Если 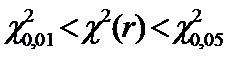 , то имеем неопределенность и можно использовать др. критерии.
, то имеем неопределенность и можно использовать др. критерии.
Корреляция
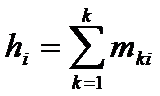 - сумма частот в i-ом столбце;
- сумма частот в i-ом столбце;
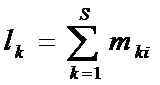 - сумма частот в к-ой строке;
- сумма частот в к-ой строке;
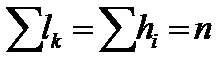 - число пар (хi ; yk).
- число пар (хi ; yk).
Условное среднее: 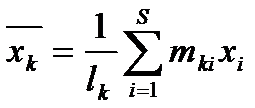 .
.
Теоретические уравнения линий регрессии:
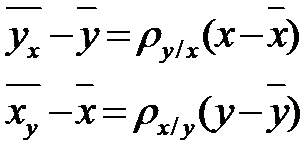 .
.
Расчет числовых характеристик:
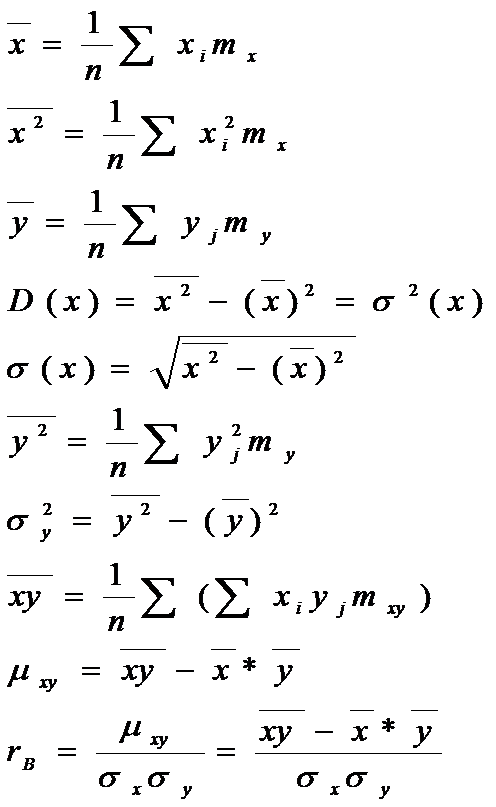
Показатель тесноты корреляционной связи – эмпирическое корреляционное отношение:
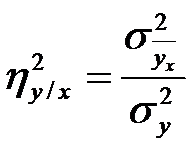 , где
, где 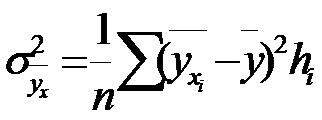 .
.
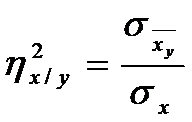 .
.
Свойства:
1. 0≤η≤1.
2. если η=1, то у(х) – связь функциональная.
3. η=0, то связи нет.
4. η≥ 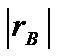 .
.
5. если η= 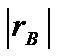 , то имеет место точная линейная корреляционная зависимость.
, то имеет место точная линейная корреляционная зависимость.
6. чем ближе η к 0, тем корреляционная связь слабее, чем ближе к 1, тем корреляционная связь сильнее и в пределе она превращается в функциональную зависимость.
Коэффициент корреляции:
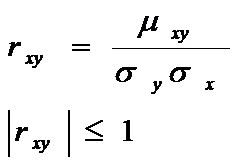 .
.
Проверка значимости параметров корреляционной зависимости:
1. Проверка существенности линейной корреляционной связи (значимости регрессии).
При больших объемах выборки коэф.корреляции подчиняется нормальному закону. При этом 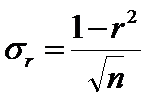 .
.
2. Проверка значимости регрессии:
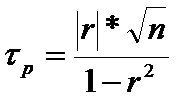 .
.
Если τр>2,58, то с уверенностью 99% можно утверждать, что корреляционная зависимость существенна (регрессия значима). Т.е. корреляционная связь существует не только в выборке, но и во всей генеральной совокупности.
τр<1,96, то с уверенностью 95% можно утверждать, что корреляционная зависимость не явл. существенной, т.е. она характерна только для данной выборки и может не существовать в генеральной совокупности.
1,96<τр< 2,58 – несущественная корреляционная зависимость.
3. Проверка линейности выбранной модели (проверка адекватности):
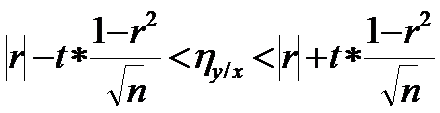 .
.
Р=99% (α=0,01): t=2,58
Р=95% (α=0,05): t=1,96
Если величина ηу/х удовлетворяет этому неравенству, то выбранная модель адекватна, она соответствует эмпирическим данным.
Критерий Фишера:
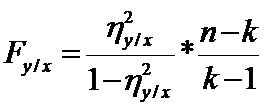 , п – число наблюдений, к – число интервалов по Х.
, п – число наблюдений, к – число интервалов по Х.
При уровнях значимости:
α=0,05 и α=0,01: F0,05(k-1;n-1); F0,01(k-1;n-k).
Если Fy/x<F0,05, то регрессия значима. Корреляционная зависимость несущественна.
Проверка значимости регрессии:
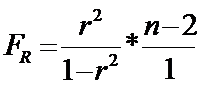 , по табл. F0,01(1;n-2), F0,05(1;n-2).
, по табл. F0,01(1;n-2), F0,05(1;n-2).
Если FR>F0,01, то регрессия значима, если FR<F0,05, то корреляционная зависимость несущественна. Если F0,05<FR<F0,01, то регрессия не явл значимой.
Адекватность модели по Фишеру:
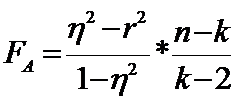 .
.
F0,01(k-2;n-k), F0,05(k-2;n-k).
Если FA>F0,01, то модель неадекватна, если FA<F0,05, то модель адекватна.
Критерий Романовского:
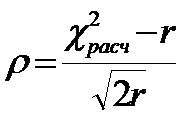 , где r – число ступеней свободы. Если ρ<3, то расхождение между теоретическими и эмпирическими распределениями нужно считать незначительными.
, где r – число ступеней свободы. Если ρ<3, то расхождение между теоретическими и эмпирическими распределениями нужно считать незначительными.
Критерий согласованности Калмагорова:
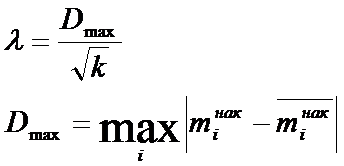 - наибольшая по абсолютной величине разность между накопленными частотами эмпирического и теоретического распределения.
- наибольшая по абсолютной величине разность между накопленными частотами эмпирического и теоретического распределения.
к – количество интервалов.
По таблице находим соответствующее значение вероятности Р(λ). Если Р(λ)<0,05, то расхождение между распределениями существенно, оно не может быть вызвано случайными причинами. Чем ближе эта вероятность к 1, тем лучше теоретическое распределение согласовывается с эмпирическим.
Теория вероятности
Комбинаторика
Соединения:
1. Перестановка: Pn=n!
2. Сочетания: 

3. Размещения: 
Свойства сочетаний:
1. 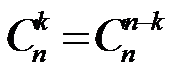
2. 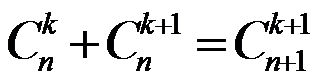
3. 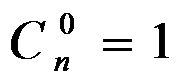
4. 0! = 1; 1!=1.
Сумма событийА и В– такое событие С, которое состоит в появлении или А, или В, или и А, и В одновременно: А+В=С=А 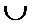 В.
В.
Произведение событийА и В – такое событие С, которое состоит в том, что появляется и А, и В одновременно.
Законы:
1. (А+В)*С=АС+ВС – ассоциативный закон.
2. А*В=В*А; А+В=В+А – коммутативный закон.
События Аj составляют полную группу событий, если они попарно несовместны и в опыте одно из них обязательно произойдет:
1) Аi*Aj=Ø  i, j
i, j
2) A1+A2+…+An= 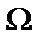
Относительная частота события:
W(A)=m/n
Классическое определение вероятности:
P(A)= W(A)=m/n
События равновозможные, если в условиях опыта ни одно из этих событий не является более вероятным, чем др.
Единовозможные события – события, кроме которых не могут произойти никакие др.
Геометрическое определение вероятности:
P(g)=mesg/mesG
Аксиомы ТВ:
1. Р(А)  0
0
2. P(  )=1
)=1
3. P(Ø)=0
4. P(A+B)=P(A)+P(B), А, В – несовместные.
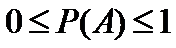
Зависимые событияА и В – это события, вероятность одного из которых меняется в зависимости от того, произошло др. событие или нет, в противоположном случае они независимы.
Условной вероятностьюназывается вероятность события В при условии, что событие А наступило:
PA(B)=P(AB)/P(A)
Теорема умножения вероятностей:
P(AB)=P(A)*PA(B) – вероятность появления 2-х событий А и В равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что 1-ое событие уже наступило.
P(AB)=P(A)*PA(B)=P(B)*PB(A)
Если А и В независимы Р(АВ)=Р(А)*Р(В).
Если 3 события А, В, С независимы Р(АВС)=Р(А)*Р(В)*Р(С).
Если А, В, С зависимы Р(АВС)=Р(А)*РА(В)*РАВ(С).
Несколько событий называются попарно независимыми, если каждые 2 из них независимы.
Несколько событий независимы в совокупности, если независимы каждые 2 из них и независимы каждое событие и все возможные произведения остальных.
Теорема сложения:
Вероятность появления одного из нескольких попарно независимых событий равна сумме вероятностей этих событий:
P(A1+…+An)= 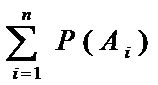 .
.
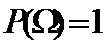
 .
.
Вероятность появления хотя бы одного из п событий  независимых в совокупности равна разности между единицей и произведением вероятности противоположных событий:
независимых в совокупности равна разности между единицей и произведением вероятности противоположных событий:
 .
.
Два события называют совместными, если появление одного из них не исключает появление другого в одном и том же испытании.
Теорема. Вероятность появления хотя бы одного из 2-х совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
Р(А+В)=Р(А)+Р(В)-Р(АВ).
Независимые события:
Р(АВ)=Р(А)*Р(В)
Р(А+В)=Р(А)+Р(В)-Р(А)*Р(В).
Зависимые события:
Р(А+В)=Р(А)+Р(В)-Р(А)*РА(В).
Несовместные события:
А*В=Øи Р(АВ)=0 → Р(А+В)=Р(А)+Р(В).
Формула полной вероятности
Теорема. Вероятность события А, которое может наступить при условии появления одного из несовместных событий В1, В2,…,Вп, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А:
P(A)= 
Формула Байеса
Формула Байеса позволяет переоценить вероятности гипотез после того, как становится известным результат испытания, в котором появилось событие А:
 .
.
Схема однородных независимых испытаний
(Бернулли, Лаплас, Пуассон)
№1. Стрелок стреляет по мишени п раз. Вероятность попадания при й выстреле равна р. Найти вероятность того, что он попадет ровно к раз – найти Рп(к).
Формула Бернулли:
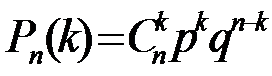 , q=1-p при п=10 (в десятках).
, q=1-p при п=10 (в десятках).
Асимптотическая формула Лапласа (дифференциальная):
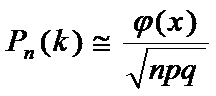 , где
, где  , п=100 (в сотнях)
, п=100 (в сотнях)
φ(х) – дифференциальная функция Лапласа.
φ(4)=0,0001
φ(5)=0,
х>7 φ(х)≈0.
Формула Пуассона:
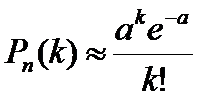 , где а=пр.
, где а=пр.
№2. Найти вероятность того, что стрелок попадет в цель не менее к1 раз и не более к2 раз.
Рп(к1, к2)= Р(к1)+Р(к1+1)+…+Р(к2).
Вероятность того, что событие наступит:
А) менее к раз: Рп(0)+Рп(1)+…+Рп(к-1);
Б) более к раз: Рп(к+1)+Рп(к+2)+…+Рп(п);
В) не менее к раз: Рп(к)+Рп(к+1)+…+Рп(п);
Г) не более к раз: Рп(0)+Рп(1)+…+Рп(к).
Интегральная формула Лапласа:
Рп(к1;к2) 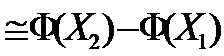 , где
, где
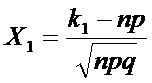 ,
,  . п≥100.
. п≥100.
Ф(- 4)≈ - 0,5; Ф(4)≈0,5.
