Основная терминология в алгебре событий.
Случайные события
Частота и вероятность
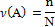
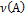 — частота события A, N — количество экспериментов, n — количество экспериментов, при которых произошло событие A.
— частота события A, N — количество экспериментов, n — количество экспериментов, при которых произошло событие A.
Статистическая устойчивость — это когда частота сходится:
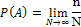
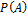 — вероятность события
— вероятность события 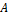 .
.
Вероятностные схемы
Классическая вероятностная схема. Это всякий опыт, для которого множество всех исходов — это конечное множество равновероятных событий.
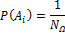
Где 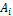 — событие, заключающееся в осуществлении одного из исходов,
— событие, заключающееся в осуществлении одного из исходов, 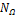 — число всех исходов.
— число всех исходов.
Геометрические вероятности. Точка бросается на плоскую область 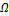 . Вероятность того, что она попадёт в определённую область
. Вероятность того, что она попадёт в определённую область 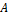 определяется как:
определяется как:
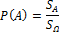
Где 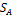 — площадь области
— площадь области 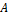 ,
, 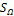 — площадь области
— площадь области 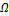 .
.
Алгебра событий
Объединением двух событий 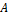 и
и 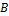 называется третье событие
называется третье событие 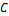 , состоящее в том, что произошло хотя бы одно из событий
, состоящее в том, что произошло хотя бы одно из событий 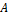 или
или 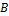 .Обозначается:
.Обозначается:
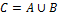 или
или 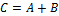
Свойства объединения:
Коммутативность: 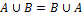
Ассоциативность: 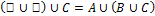
Пересечением двух событий 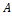 и
и 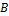 называется третье событие
называется третье событие 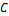 , состоящее в том, что произошли оба события
, состоящее в том, что произошли оба события 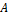 и
и 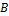 .Обозначается:
.Обозначается:
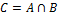 или
или 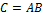
Свойства пересечения:
Коммутативность: 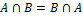
Ассоциативность: 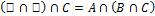
Общие свойства:
Дистрибутивность относительно пересечения: 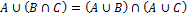
Дистрибутивность относительно объединения: 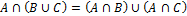
Алгебра событий — такая система событий F, для которой любое пересечение, объединение и дополнение любых двух событий, принадлежащих F, так же принадлежит F.
Основная терминология в алгебре событий.
Невозможное событие — событие A, для которого 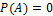 . Обозначается ∅.
. Обозначается ∅.
Достоверное событие — событие A, для которого 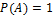 . Обозначается E.
. Обозначается E.
Противоположные события — события 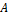 и
и  .
.
Несовместные события — события A и B, для которых 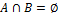 .
.
Полная группа — множество событий 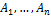 , для которых
, для которых
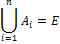
Независимые события — события A и B такие, что 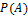 не зависит от того, произошло событие B или нет, и
не зависит от того, произошло событие B или нет, и 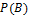 не зависит от того, произошло событие A или нет.
не зависит от того, произошло событие A или нет.
A называется следствиемB, если A происходит всякий раз, когда происходит B. Обозначается 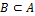 или
или 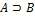 .
.
Эквивалентные события — события A и B, для которых 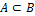 и
и 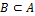 . Обозначается
. Обозначается 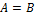 .
.
Разность событий (A и B) — событие C, состоящее в том, что A произошло, а B не произошло. Обозначается 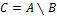 . Из определения следует:
. Из определения следует:
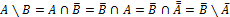
Принцип двойственности
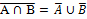
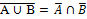
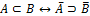
A и B — события.
Условная вероятность
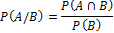
Где 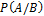 — вероятность события A при условии, что B произошло.
— вероятность события A при условии, что B произошло.
Формула сложения вероятностей
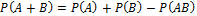
Если события A и B несовместные, то:
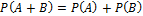
A и B — события.
Формула умножения вероятностей
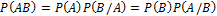
Если события A и B независимые, то:
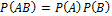
Обобщение формулы сложения вероятностей
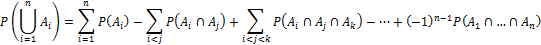
Если события 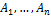 несовместные, то:
несовместные, то:
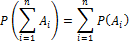
Обобщение формулы умножения вероятностей
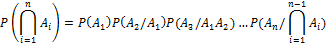
Если 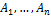 независимые в совокупности, то:
независимые в совокупности, то:
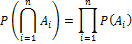
Формулаполной вероятности
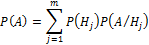
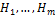 — полная группа независимых событий,
— полная группа независимых событий, 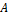 — произвольное событие.
— произвольное событие.
Формула Байеса
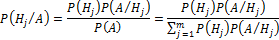
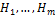 — полная группа независимых событий,
— полная группа независимых событий, 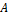 — произвольное событие.
— произвольное событие.
Аксиомы теории вероятностей
Пусть 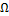 — пространство элементарных событий, F — алгебра событий (алгебра подмножеств множества F). Аксиомы:
— пространство элементарных событий, F — алгебра событий (алгебра подмножеств множества F). Аксиомы:
1. Система событий F является σ-алгеброй событий.
Система событий F является σ-алгеброй, если пересечение, объединение и дополнение любой бесконечной последовательности событий, принадлежащих F, так же принадлежит F.
2. Аксиома существования вероятности. На σ-алгебре событий F для любого 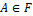 определяется функция
определяется функция 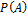 , называемая вероятностью и принимающая значения от 0 до 1 включительно.
, называемая вероятностью и принимающая значения от 0 до 1 включительно.
3. Аксиома сложения вероятностей. Для любых двух несовместных событий A и B: 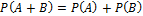 .
.
А так же для любого конечного числа несовместных событий: 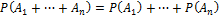 .
.
4. Аксиома счётной аддитивности (непрерывной вероятности). Пусть все события 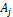 попарно несовместные, тогда:
попарно несовместные, тогда:
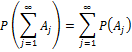
5. 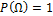 . Эта аксиома указывает на то, что пространство элементарных событий
. Эта аксиома указывает на то, что пространство элементарных событий 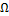 — достоверное событие.
— достоверное событие.
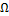 , F и P образуют вероятностное пространство , которое обозначают
, F и P образуют вероятностное пространство , которое обозначают 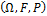 .Система аксиом не противоречива и не полна.
.Система аксиом не противоречива и не полна.
Комбинаторика: перестановки
Имеется множества из 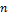 разных объектов. Число вариантов последовательностей в которых их можно расположить:
разных объектов. Число вариантов последовательностей в которых их можно расположить: 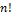 .
.
Комбинаторика: размещения
Имеется множества из 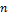 разных объектов. Из них выбираются
разных объектов. Из них выбираются 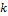 (
( 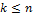 ) объектов. Порядок выбранных объектов имеет значение.
) объектов. Порядок выбранных объектов имеет значение.
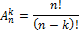
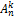 — число вариантов выбранных последовательностей.
— число вариантов выбранных последовательностей.
Комбинаторика: сочетания
Имеется множества из 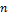 разных объектов. Из них выбираются
разных объектов. Из них выбираются 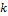 (
( 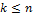 ) объектов.Порядок выбранных объектов не имеет значение.
) объектов.Порядок выбранных объектов не имеет значение.
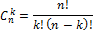
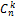 — число вариантов выбранных множеств.
— число вариантов выбранных множеств.
Асимптотика Пуассона
Возьмём вероятностную схему Бернулли (серия одинаковых опытов с исходом успех или неудача). Рассмотрим её при условии, что число опытов 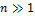 , а вероятность успеха
, а вероятность успеха 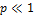 , тогда можно воспользоваться упрощённой формулой (формулой Пуассона) для приблизительного вычисления вероятности того, что в
, тогда можно воспользоваться упрощённой формулой (формулой Пуассона) для приблизительного вычисления вероятности того, что в 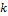 случаях из
случаях из 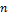 будет успех:
будет успех:
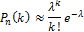
Где 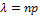 . При
. При 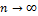 :
:
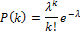
Случайные величины
Примеры распределения случайной величины
1. Равномерное.
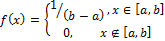
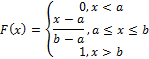
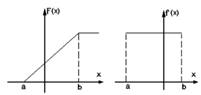
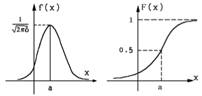
2. Нормальное (гауссовое).
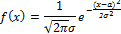
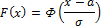
Где 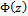 — функция Лапласа.
— функция Лапласа.
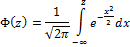
3. Коши.
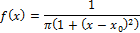
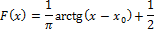
4. Экспоненциальное распределение.
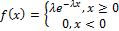
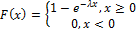
Примеры математического ожидания
1. Равномерное распределение.
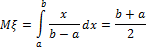
2. Нормальное распределение.
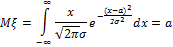
3. Схема Бернулли.
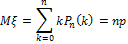
Примеры дисперсии
1. Нормальное распределение.
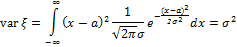
2. Экспоненциальное распределение.
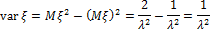
3. Схема Бернулли.
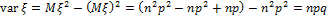
Моменты случайных величин
Начальный момент k-го порядка:
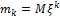
Для непрерывной величины:
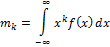
Для дискретной величины:
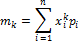
Центральный момент k-го порядка:
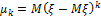
Для непрерывной случайной величины:
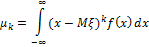
Для дискретной случайной величины:
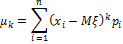
Неравенство Чебышева
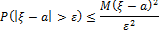
Где 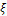 — случайная величина,
— случайная величина, 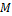 — оператор математического ожидания,
— оператор математического ожидания, 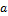 и
и 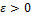 — произвольные параметры.
— произвольные параметры.
Коэффициент асимметрии
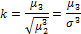
Где 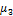 — центральный момент третьего порядка,
— центральный момент третьего порядка, 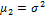 — центральный момент второго порядка (дисперсия).
— центральный момент второго порядка (дисперсия).
Коэффициент эксцесса
Характеризует степень сглаженности вершины плотности вероятности.
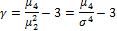
Где 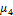 — центральный момент четвёртого порядка,
— центральный момент четвёртого порядка, 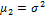 — центральный момент второго порядка (дисперсия).
— центральный момент второго порядка (дисперсия).
Чем больше 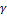 , тем острее вершина, у нормального распределения
, тем острее вершина, у нормального распределения 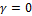 .
.
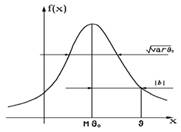
Среднеквадратическая ошибка
Пусть 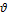 (буква — тэта) — неизвестный параметр системы, который измеряют. Результат измерения есть случайная величина
(буква — тэта) — неизвестный параметр системы, который измеряют. Результат измерения есть случайная величина 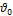 (оценка параметра
(оценка параметра 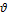 ).
).
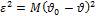
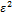 — среднеквадратичная ошибка (похоже на дисперсию, но не оно, потому что
— среднеквадратичная ошибка (похоже на дисперсию, но не оно, потому что 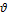 — не математическое ожидание).
— не математическое ожидание).
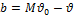
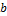 — смещение оценки
— смещение оценки 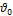 .
.
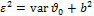
Где 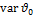 дисперсия величины
дисперсия величины 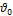 .
.
Характеристическая функция
Характеристическая функция случайной величины 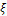 :
:
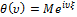
Для непрерывной случайной величины с плотностью вероятности 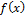 :
:
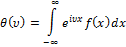
Это выражение так же называется преобразованием Фурье. Возможно обратное преобразование:
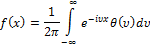
Для дискретной случайной величины со значениями 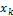 и с соответствующими вероятностями
и с соответствующими вероятностями 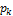 :
:
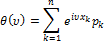
Кумулянтная функция
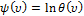
Где 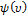 — кумулянтная функция,
— кумулянтная функция, 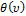 — характеристическая функция.
— характеристическая функция.
Кумулянтную функцию можно разложить в ряд Тейлора в близи точки 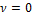 :
:
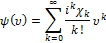
Где 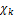 — кумулянт k-го порядка случайной величины
— кумулянт k-го порядка случайной величины 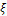 :
:
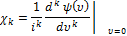
Случайные векторы
Коэффициент корреляции
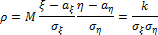
Где 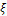 и
и 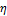 — случайные величины,
— случайные величины, 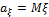 ,
, 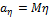 ,
, 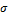 — дисперсия,
— дисперсия, 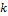 — ковариация.
— ковариация.
Чем ближе 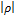 к 1, тем сильнее связь между случайными величинами, чем
к 1, тем сильнее связь между случайными величинами, чем 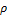 ближе к 0, тем слабее связь.
ближе к 0, тем слабее связь.
Случайные события
Частота и вероятность
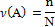
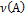 — частота события A, N — количество экспериментов, n — количество экспериментов, при которых произошло событие A.
— частота события A, N — количество экспериментов, n — количество экспериментов, при которых произошло событие A.
Статистическая устойчивость — это когда частота сходится:
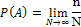
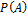 — вероятность события
— вероятность события 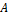 .
.
Вероятностные схемы
Классическая вероятностная схема. Это всякий опыт, для которого множество всех исходов — это конечное множество равновероятных событий.
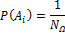
Где 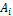 — событие, заключающееся в осуществлении одного из исходов,
— событие, заключающееся в осуществлении одного из исходов, 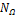 — число всех исходов.
— число всех исходов.
Геометрические вероятности. Точка бросается на плоскую область 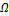 . Вероятность того, что она попадёт в определённую область
. Вероятность того, что она попадёт в определённую область 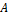 определяется как:
определяется как:
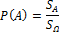
Где 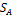 — площадь области
— площадь области 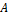 ,
, 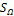 — площадь области
— площадь области 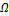 .
.
Алгебра событий
Объединением двух событий 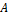 и
и 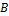 называется третье событие
называется третье событие 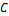 , состоящее в том, что произошло хотя бы одно из событий
, состоящее в том, что произошло хотя бы одно из событий 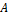 или
или 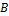 .Обозначается:
.Обозначается:
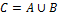 или
или 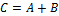
Свойства объединения:
Коммутативность: 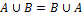
Ассоциативность: 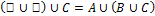
Пересечением двух событий 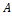 и
и 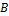 называется третье событие
называется третье событие 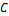 , состоящее в том, что произошли оба события
, состоящее в том, что произошли оба события 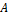 и
и 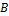 .Обозначается:
.Обозначается:
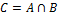 или
или 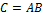
Свойства пересечения:
Коммутативность: 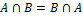
Ассоциативность: 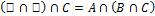
Общие свойства:
Дистрибутивность относительно пересечения: 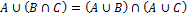
Дистрибутивность относительно объединения: 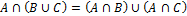
Алгебра событий — такая система событий F, для которой любое пересечение, объединение и дополнение любых двух событий, принадлежащих F, так же принадлежит F.
Основная терминология в алгебре событий.
Невозможное событие — событие A, для которого 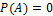 . Обозначается ∅.
. Обозначается ∅.
Достоверное событие — событие A, для которого 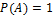 . Обозначается E.
. Обозначается E.
Противоположные события — события 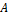 и
и  .
.
Несовместные события — события A и B, для которых 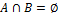 .
.
Полная группа — множество событий 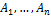 , для которых
, для которых
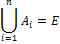
Независимые события — события A и B такие, что 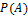 не зависит от того, произошло событие B или нет, и
не зависит от того, произошло событие B или нет, и 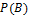 не зависит от того, произошло событие A или нет.
не зависит от того, произошло событие A или нет.
A называется следствиемB, если A происходит всякий раз, когда происходит B. Обозначается 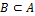 или
или 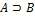 .
.
Эквивалентные события — события A и B, для которых 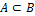 и
и 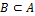 . Обозначается
. Обозначается 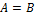 .
.
Разность событий (A и B) — событие C, состоящее в том, что A произошло, а B не произошло. Обозначается 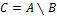 . Из определения следует:
. Из определения следует:
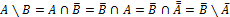
Принцип двойственности
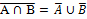
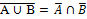
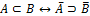
A и B — события.
Условная вероятность
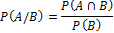
Где 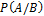 — вероятность события A при условии, что B произошло.
— вероятность события A при условии, что B произошло.
