Резонансы в цепях переменного тока.

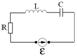
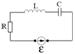
Резонанс напряжений. Рассмотрим схему:

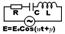
Найдём ток текущий в цепи. По закону Ома для цепей с переменным током имеем:

.

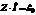Откуда имеем следующее выражение для амплитуды тока: .

Очевидно, что максимальная амплитуда тока будет при минимальности знаменателя, т.е. при 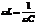. Т.о. - резонансная частота. При резонансной частоте , а .

При .

При .

Т.о. при ток будет отставать от ЭДС, но при ток будет опережать ЭДС.

Вид зависимости амплитуды тока от частоты вынуждающей силы.

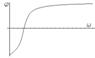
Резонанс токов.

Рассмотрим контур.

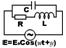
Пусть 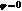. Тогда Имеем для тока текущего через ЭДС:

,

.

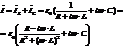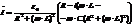Мнимая часть амплитуды тока будет равна нулю при 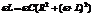. При этом условии данная катушка обладает чисто омическим сопротивлением т.е. и находятся в фазе, т.е. имеет место быть резонанс (так говорят в схемотехнике).

.

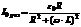При резонансе токов ток через генератор минимален.

В очередной раз рассмотрим следующий контур

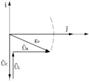
Стрелка указывает направления ЭДС в начальный момент времени.

Изобразим на одном графике зависимости напряжений на сопротивлении, катушке и конденсаторе в зависимости от частоты подаваемого напряжения .

На всех трех графиках возникает максимум при частоте близкой к резонансной .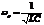

Теперь рассмотрим следующую схему:

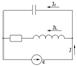
Ранее нами уже было получено выражение для комплексной амплитуды силы тока в цепи .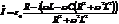

Видим, что при условии 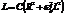данная цепочка будет обладать чисто омическим сопротивлением. Ток и ЭДС находятся в фазе. В этом случае говорят о резонансе токов. В случае 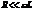эту резонансную частоту можно приближенно считать равной 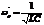. Но истинная резонансная частота зависит от добротности 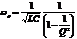, где 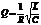. Найдем значения токов в ветвях контура при резонансной частоте. .

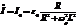Рассмотрим случай 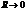, тогда 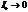. Полный ток в цепи равен нулю. При этом ток в цепи с конденсатором не нулевой. 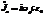и опережает ЭДС по фазе на 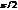. Ток в ветви с катушкой 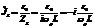отстает от ЭДС на 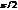. Токи через катушку и конденсатор совпадают по амплитуде, но противоположно направлены.

В идеальном контуре токи в ветвях с конденсатором и индуктивностью достигают достаточно больших значений и протекают в противоположных направлениях. Начальная энергия, которой обладает колебательный контур при резонансе, была получена сразу после замыкания ключа в процессе установления.

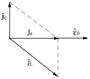
Проиллюстрируем на векторных диаграммах случаи резонанса напряжений.

Подаваемое на цепочку напряжение равно сумме напряжений на конденсаторе, сопротивлении и индуктивности 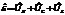. Каждой из этих комплексных величин ставится в соответствие вектор на комплексной плоскости 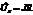, , 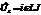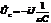. Цепь не разветвленная, значит, во всех элементах цепи течет одинаковый ток.

Пусть начальная фаза тока равна нулю и . Если величина достаточно мала, то величина 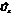тоже мала. При увеличении вектор 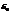будет разворачиваться, и при совпадении с направлением 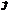наступит резонанс.

Построим векторную диаграмму токов при нулевом сопротивлении. За нуль возьмем фазу ЭДС 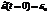. Учтем, что по первому правилу Кирхгофа, сумма токов равна нулю .

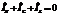При резонансе .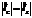

Если сопротивление не равно нулю, то получим следующую диаграмму токов.