Производная и дифференциалы высших порядков.
Рассмотрим функцию 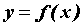 , определенную на некотором промежутке
, определенную на некотором промежутке 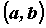 . Вычислим производную
. Вычислим производную 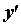 , которая также является функцией на
, которая также является функцией на  . Производной второго порядка от функции
. Производной второго порядка от функции 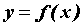 называется производная от ее производной:
называется производная от ее производной: 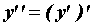 . Аналогично определяют производную любого порядка:
. Аналогично определяют производную любого порядка: 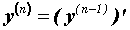 .
.
Рассмотрим дифференциал функции 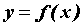 в произвольной точке промежутка
в произвольной точке промежутка 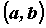 :
: 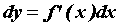 . Здесь
. Здесь 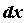 - приращение независимой переменной, которое является числом и не зависит от
- приращение независимой переменной, которое является числом и не зависит от 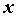 . Сам же дифференциал есть функция от
. Сам же дифференциал есть функция от 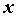 , и можно вычислить дифференциал от этой функции:
, и можно вычислить дифференциал от этой функции: 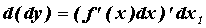 При
При 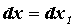 этот дифференциал от дифференциала называется дифференциалом второго порядка и вычисляется по формуле
этот дифференциал от дифференциала называется дифференциалом второго порядка и вычисляется по формуле 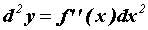 Аналогично вычисляется дифференциал любого порядка
Аналогично вычисляется дифференциал любого порядка 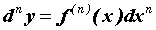 .
.
Теорема Ферма.
Теорема утверждает, что:
Для любого натурального числа n > 2уравнение 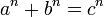 не имеет натуральных решений a, b и c. не имеет натуральных решений a, b и c. |
Теорема Ролля.
Теорема Ро́лля (теорема о нуле производной) утверждает, что Если функция непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b), принимает на концах этого интервала одинаковые значения, то на этом интервале найдётся хотя бы одна точка, в которой производная функции равна нулю.
Теорема Лагранжа.
Формула конечных приращений или теорема Лагра́нжа о среднем значении утверждает, что если функция f непрерывна на отрезке[a;b] и дифференцируема в интервале (a;b), то найдётся такая точка 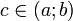 , что
, что
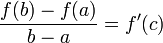 .
.
Геометрически это можно переформулировать так: на отрезке [a;b] найдётся точка, в которой касательная параллельна хорде, проходящей через точки графика, соответствующие концам отрезка.
Механическое истолкование: Пусть f(t) — расстояние точки в момент t от начального положения. Тогда f(b) − f(a) есть путь, пройденный с момента t = a до момента t = b, отношение 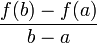 — средняя скорость за этот промежуток.
— средняя скорость за этот промежуток.
Теорема Коши.
Пусть функции f(x) и g(x)
- непрерывны на отрезке [a, b];
- дифференцируемы в интервале (a, b);
| f '(c) |
| g '(c) |
- "x О (a, b) g'(x) ≠ 0 .
| |
| g(b) − g(a) |
Тогда существует точка c О (a, b) такая, что
Правило Лопиталя.
Правило Лопита́ля — метод нахождения пределов функций, раскрывающий неопределённости вида 0 / 0 и 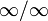 . Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.
. Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.
Условия:
1. 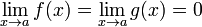 или
или 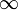 ;
;
2. 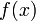 и
и 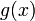 дифференцируемы в проколотой окрестности
дифференцируемы в проколотой окрестности 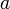 ;
;
3. 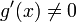 в проколотой окрестности
в проколотой окрестности 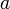 ;
;
4. существует 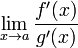 ,
,
тогда существует 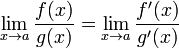 .
.
Пределы также могут быть односторонними.
Формулы Тейлора и Маклорена.
Если функция f (x) имеет непрерывные производные вплоть до (n+1)-го порядка, то ее можно разложить в степенной ряд по формуле Тейлора:
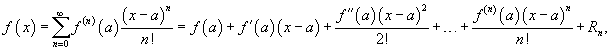
где Rn − остаточный член в форме Лагранжа определяется выражением
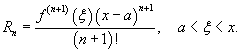
Если приведенное разложение сходится в некотором интервале x, т.е. 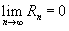 , то оно называется рядом Тейлора, представляющим разложение функции f (x) в точке a.
, то оно называется рядом Тейлора, представляющим разложение функции f (x) в точке a.
Если a = 0, то такое разложение называется рядом Маклорена:
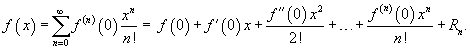
Разложение функций в ряд Маклорена.
· 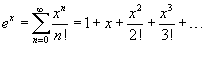 · · 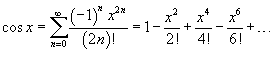 · · 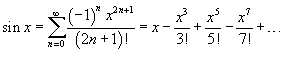 · · 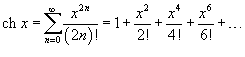 · · 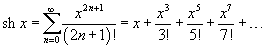 |
