Бесконечно большие функции и их связь с БМФ.

Бесконечно большая— числовая функция, которая стремится к бесконечности определённого знака.

Функция называется бесконечно большой в окрестности точки x₀, если .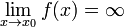

Функция называется бесконечно большой на бесконечности, если 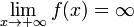либо .

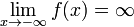Сравнение бесконечно малых функций.

Допустим, у нас есть бесконечно малые при одном и том же 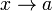величины α(x) и β(x) (либо, что не важно для определения, бесконечно малые последовательности).

• Если 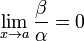, то β — бесконечно малая высшего порядка малости, чем α. Обозначают β = o(α).
• Если 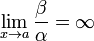, то β — бесконечно малая низшего порядка малости, чем α. Соответственно α = o(β).
• Если 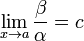(предел конечен и не равен 0), то α и β являются бесконечно малыми величинами одного порядка малости. Это обозначается как β = O(α) или α = O(β) (в силу симметричности данного отношения).

· Если 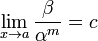(предел конечен и не равен 0), то бесконечно малая величина β имеет m-й порядок малости относительно бесконечно малой α.

Непрерывность функции в точке, интервале и отрезке и их св-ва.

Рассмотрим функцию 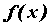, определенную на некотором промежутке 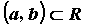. Функция 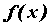непрерывна в точке 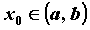, если предел функции в точке 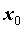равен значению функции в этой точке, .

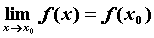Свойства: Функция, непрерывная в каждой точке промежутка 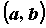, называется непрерывной на промежутке. Для функции, непрерывной на отрезке 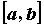, справедливы следующие утверждения.

Функция, непрерывная на отрезке 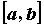, достигает на нем своих наибольшего и наименьшего значений, т.е. на отрезке 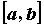существуют точки 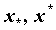такие, что

.

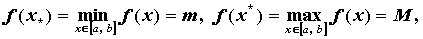
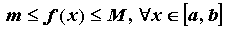Если функция 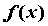непрерывна на отрезке 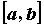и принимает на концах значения разных знаков, то на интервале 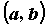существует точка 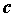, в которой функция обращается в нуль, т.е. 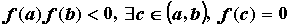. Это утверждение применяют для отделения корней уравнений 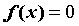с непрерывной левой частью — если найден отрезок, на концах которого функция принимает значения разных знаков, то можно утверждать, что на этом отрезке есть хотя бы один корень уравнения.

Если функция 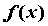непрерывна на отрезке 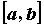, дифференцируема хотя бы на интервале 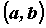, то на интервале 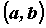существует точка 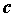, такая, что 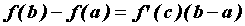. Это свойство называют формулой Лагранжа или формулой конечных приращений.

Точки разрыва и их классификация.

Если хотя бы одно из равенств 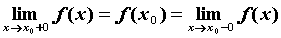нарушается, говорят о разрыве в точке 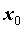. Если 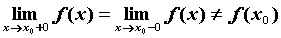и односторонние пределы конечны, то разрыв в точке 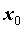называется устранимым. Если 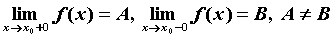и оба односторонние пределы конечны, то говорят о скачке функции в точке 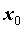. Устранимый разрыв и скачок называются разрывами первого рода. Если один из односторонних пределов бесконечен или не существует, то разрыв называется разрывом второго рода. Так же, как для предела и непрерывности, говорят о разрыве слева и разрыве справа.

Понятие производной.

Пусть функция 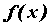определена на промежутке 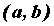. Точка 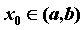— произвольная точка из области определения функции, 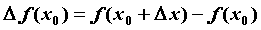— приращение функции в точке 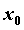, вызванное приращением 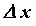независимой переменной 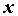Производнойфункции 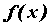по независимой переменной 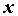в точке 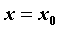, 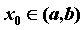называется предел отношения приращения функции 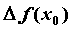к приращению 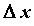при стремлении 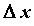к нулю, т.е.

,

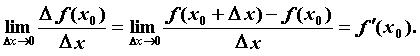
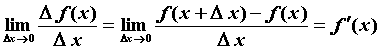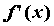— производная функции в точке .

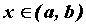Правила дифференцирования.

Пусть функция 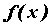определена в некоторой окрестности точки 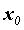. Рассмотрим приращение функции в этой точке: 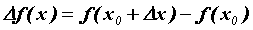. Функция 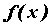называется дифференцируемой в точке , если ее приращение можно записать в ви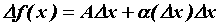де , где 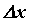- приращение независимой переменной, А – постоянная, не зависящая от 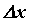, 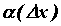- бесконечно малая функция при .

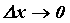Дифференциалом функции 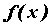в точке 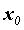называется линейная по 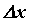часть 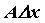приращения 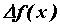. Дифференциал обозначается 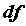, то есть 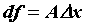. Рассматривая функцию 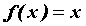, нетрудно убедиться, что 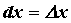, если 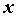- независимая переменная.

Воспользуемся определением производной для дифференцируемой функции 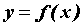в точке 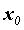: 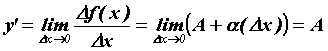. Таким образом, дифференциал функции выражается формулой 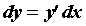, то есть для вычисления дифференциала необходимо лишь вычислить производную и умножить ее на 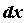. Поэтому часто слова “вычисление производной” и “дифференцирование” считают синонимами. Для того, чтобы функция была дифференцируема в точке, необходимо и достаточно, чтобы в этой точке существовала конечная производная.