Ханты-мансийского автономного округа-югра»
ГОУ ВПО
«Сургутский государственный университет
Ханты-Мансийского автономного округа-Югра»
И.В.Шапошникова
МАТЕМАТИЧЕСКИЙ АНАЛИЗ
Часть 1
И.В.Шапошникова
Математический анализ. Часть 1: Учебно-методическое пособие для студентов заочной формы обучения спец. 080109 «Бухгалтерский учёт, анализ и аудит». -
Учебно-методическое пособие предназначено для студентов первого курса заочного факультета спец. 080109 «Бухгалтерский учёт, анализ и аудит» и содержит программу курса математического анализа, утверждённую методическим Советом университета, общие рекомендации студенту-заочнику по изучению данной дисциплины, список литературы, контрольные задания (10 вариантов) и вопросы для самопроверки по разделам курса Поскольку издание преследует сугубо учебно-методические цели, то оно носит компилятивный характер.
ОБЩИЕ РЕКОМЕНДАЦИИ СТУДЕНТУ-ЗАОЧНИКУ ПО РАБОТЕ НАД КУРСОМ ВЫСШЕЙ МАТЕМАТИКИ.
Основной формой обучения студента-заочника является самостоятельная работа над учебным материалом, которая состоит из изучения материала по учебникам, решения задач, выполнения контрольных работ, ответов на вопросы для самопроверки. В помощь студентам-заочникам кафедра высшей математики СурГУ организует чтение обзорных лекций, консультации в течение семестра и перед экзаменом (зачетом). Кроме того, студент может обращаться к преподавателю с вопросами в письменном или устном виде. Указания студенту по текущей работе даются также в процессе рецензирования контрольных работ. Однако студент должен помнить, что только при систематической и упорной самостоятельной работе помощь кафедры окажется достаточно эффективной.
Завершающим этапом изучения отдельных частей курса математического анализа является сдача экзаменов и зачетов в соответствии с учебным планом.
КОНТРОЛЬНЫЕ РАБОТЫ.
В процессе изучения курса математического анализа студент должен выполнить ряд контрольных работ, главная цель которых – оказать студенту помощь в его работе. Рецензии преподавателя позволяют студенту судить о степени усвоения им соответствующего раздела курса, указывают на имеющиеся у него пробелы. При выполнении контрольных работ студент должен руководствоваться следующими указаниями:
1. Не следует приступать к выполнению контрольного задания, не решив достаточного количества задач по материалу, соответствующему этому заданию. Опыт показывает, что затруднение при решении той или иной задачи контрольного задания вызвано тем, что студент не выполнил этого требования.
2. Каждую контрольную работу следует выполнять в отдельной тетради. Желательно оставлять на каждой странице широкие поля для замечаний рецензента.
3. На обложке тетради должны быть указаны фамилия и инициалы студента, учебный номер (шифр), название дисциплины, номер контрольной работы. В конце работы должны стоять дата её выполнения и подпись студента.
4. В работу должны быть включены все задачи, указанные в задании, строго по положенному варианту. Желательно оставлять на каждой странице широкие поля для замечаний рецензента.
5. Решения задач надо располагать в порядке возрастания их номеров, указанных в заданиях, сохраняя номер задачи. Перед решением задачи надо полностью выписать её условие.
6. Все вычисления должны быть приведены полностью, со ссылками на используемые формулы. Чертежи и графики должны быть выполнены аккуратно, четко, с указанием единиц масштаба и координатных осей.
7. После получения прорецензированной работы студент должен исправить в ней все ошибки. В случае незачета студент обязан в кратчайший срок выполнить все требования рецензента и предоставить исправленную работу на повторное рецензирование (исправления и дополнения к первоначальной работе обязательно выполняются в той же тетради). При отсутствии зачтенных контрольных работ студент не допускается к сессии.
8. Контрольная работа должна выполняться самостоятельно.
9. По учебному плану в первом семестре студент-заочник обязан выполнить три контрольные работы по математике согласно варианту номер которого совпадает с последней цифрой его учебного номера (шифра) (см. табл. 1).
Таблица 1
Распределение заданий по вариантам.
| Вариант | Номера задач контрольных заданий | |
| Контрольная работа № 1 | Контрольная работа № 2 | |
| 1,11,21 | 31,41,51,61, 71,81,91 | |
| 2,12,22 | 32,42,52,62, 72,82,92 | |
| 3,13,23 | 33,43,53,63, 73,83,93 | |
| 4,14,24 | 34,44,54,64, 74,84,94 | |
| 5,15,25 | 35,45,55,65, 75,85,95 | |
| 6,16,26 | 36,46,56,66, 76,86,96 | |
| 7,17,27 | 37,47,57,67, 77,87,97 | |
| 8,18,28 | 38,48,58,68, 78,88,98 | |
| 9,19,29 | 39,49,59,69, 79,89,99 | |
| 10,20,30 | 40,50,60,70, 80,90,100 |
ЗАЧЕТЫ И ЭКЗАМЕНЫ
После каждого семестра студент должен сдавать зачет или экзамен. Обычно экзамену или зачету предшествует собеседование студента с преподавателем по выполненным контрольным работам.
На зачете и экзамене от студента требуется знание определений, формулировок и доказательств теорем в объеме программы курса, знание формул и умение решать соответствующие задачи. При подготовке к экзамену рекомендуется повторить учебный материал по учебнику и конспекту.
ПРОГРАММА ДИСЦИПЛИНЫ “МАТЕМАТИЧЕСКИЙ АНАЛИЗ” (ЧАСТЬ I).
Контрольная работа №1
Контрольная работа №3
ОДНОЙ ПЕРЕМЕННОЙ.
31- 40.Найти производные 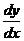 данных функций.
данных функций.
31. а) 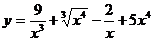 ; б)
; б) 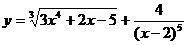 ;
;
в) 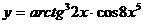 ; г)
; г) 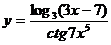 .
.
32. а) 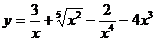 ; б)
; б) 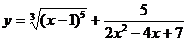 ;
;
в) 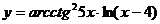 ; г)
; г) 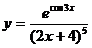 .
.
33. а) 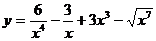 ; б)
; б) 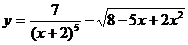 ;
;
в) 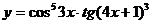 ; г)
; г) 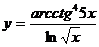 .
.
34. а) 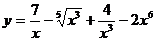 ; б)
; б) 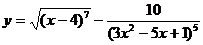 ;
;
в) 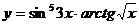 ; г)
; г) 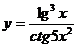 .
.
35. а) 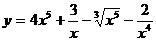 ; б)
; б) 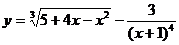 ;
;
в) 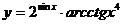 ; г)
; г) 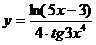 .
.
36. а) 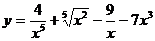 ; б)
; б) 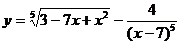 ;
;
в) 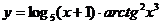 ; г)
; г) 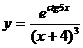 .
.
37. а) 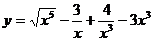 ; б)
; б) 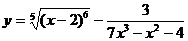 ;
;
в) 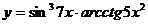 ; г)
; г) 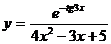 .
.
38. а) 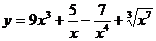 ; б)
; б) 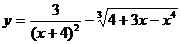 ;
;
в)  ; г)
; г) 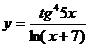 .
.
39. а) 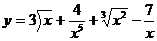 ; б)
; б) 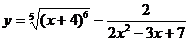 ;
;
в) 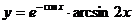 ; г)
; г) 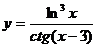 .
.
40. а) 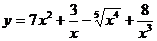 ; б)
; б) 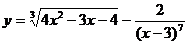 ;
;
в) 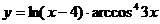 ; г)
; г) 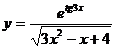 .
.
41-50.Найти 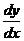 и
и 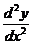 для заданных функций и вычислить их значения в данной точке х0.
для заданных функций и вычислить их значения в данной точке х0.
41. 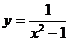 , х0 = 0.
, х0 = 0.
42.у = sin2x , x0 = p/2.
43. y = ln(2 + x2), x0 = 0.
44. y = x4 lnx, x0 = 1.
45. y = exsin2x, x0 = 0.
46. y = x sinx, x0 = p/2.
47. y = (x+1) ln(x+1), x0 = -1/2.
48. y = ln3x, x0 = 1.
49. y = e-x cosx, x0 = 0.
50. y = x2 lnx, x0 = 1/3.
51-60.Найти дифференциалы первого и второго порядка для заданных функций и вычислить их значения в заданной точке х0.
51. 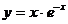 , х0 = 0.
, х0 = 0.
52. 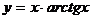 , х0 =1.
, х0 =1.
53. 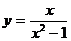 , х0 = 0.
, х0 = 0.
54. 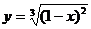 , х0 = 2.
, х0 = 2.
55. 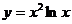 , х0 =1.
, х0 =1.
56. 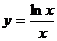 , х0 = 1.
, х0 = 1.
57. 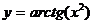 , х0 = -1.
, х0 = -1.
58. 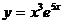 , х0 = 0.
, х0 = 0.
59. 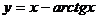 , х0 = -1.
, х0 = -1.
60. 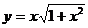 , х0 = 0.
, х0 = 0.
61-70.С помощью дифференциала вычислить приближенное значение данной величины.
61. 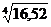 .62.tg 460.
.62.tg 460.
63. 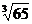 .64.arctg 1,05.
.64.arctg 1,05.
65. 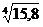 . 66.cos 590.
. 66.cos 590.
67.e2,01 . 68.ctg 440.
69. lg 11. 70.sin 1510.
71.Проверитьсправедливость теоремы Ролля для функции y = 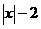 на данном отрезке [–2;2]. Найти соответствующее значение с (если оно существует).
на данном отрезке [–2;2]. Найти соответствующее значение с (если оно существует).
72. Найти точку, в которой касательная к кривой y = x2 – 4x параллельно хорде, соединяющей точки А (1, –3) и В (5,5). Сделать поясняющий рисунок.
73. Проверить справедливость теоремы Лагранжа для функции y=еx на данном отрезке [0,1]. Найти соответствующее значение с (если оно существует).
74.Дана функция y = 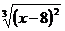 . Пусть а = 0, b = 16. Тогда y(0) = y (16) = 4. Однако производная этой функции не обращается в нуль ни в одной точке интервала (0,16). Противоречит ли это теореме Ролля?
. Пусть а = 0, b = 16. Тогда y(0) = y (16) = 4. Однако производная этой функции не обращается в нуль ни в одной точке интервала (0,16). Противоречит ли это теореме Ролля?
75. Проверитьсправедливость теоремы Ролля для функции y = –x2 + 4x –3 на данном отрезке [0,4]. Найти соответствующее значение с (если оно существует).
76. Найти точку, в которой касательная к кривой y = ln x параллельно хорде, соединяющей точки А (1, 0) и В (е,1). Сделать поясняющий рисунок.
77. Проверить справедливость теоремы Лагранжа для функции y = 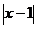 на данном отрезке [0,3]. Найти соответствующее значение с (если оно существует).
на данном отрезке [0,3]. Найти соответствующее значение с (если оно существует).
78. Проверитьсправедливость теоремы Ролля для функции y = 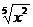 на данном отрезке [1,1]. Найти соответствующее значение с (если оно существует).
на данном отрезке [1,1]. Найти соответствующее значение с (если оно существует).
79. Проверить справедливость теоремы Лагранжа для функции y=  на данном отрезке [
на данном отрезке [ 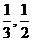 ]. Найти соответствующее значение с (если оно существует).
]. Найти соответствующее значение с (если оно существует).
80. Проверитьсправедливость теоремы Ролля для функции y = cos x на данном отрезке [ 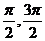 ]. Найти соответствующее значение с (если оно существует).
]. Найти соответствующее значение с (если оно существует).
81-90.Найти пределы, используя правило Лопиталя.
81. 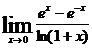 . 86.
. 86. 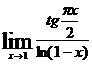 .
.
82. 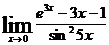 . 87.
. 87. 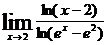 .
.
83. 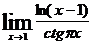 . 88.
. 88. 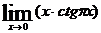 .
.
84. 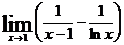 . 89.
. 89. 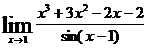 .
.
85. 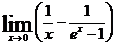 . 90.
. 90. 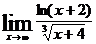
91.-100.Исследовать методами дифференциального исчисления функции 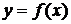 и, используя результаты исследования, построить их графики.
и, используя результаты исследования, построить их графики.
91. а) 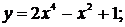 б)
б) 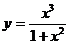
92. а) 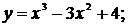 б)
б) 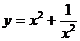
93. а) 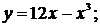 б)
б) 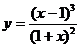
94. а) 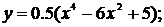 б)
б) 
95. а) 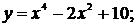 б)
б) 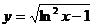
96. а) 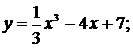 б)
б) 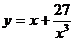
97. а) 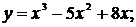 б)
б) 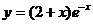
98. а) 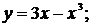 б)
б) 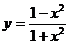
99. а) 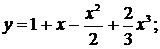 б)
б) 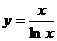
100. а) 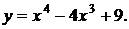 б)
б) 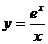
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ.
ЛИТЕРАТУРА
а) основная литература:
1. Общий курс высшей математики для экономистов: Учебник. / Под ред. В.И. Ермакова. – М.: Инфра-М, 2010.
2. Сборник задач по высшей математике для экономистов: Учеб. пособие. / Под ред. В.И.Ермакова. – 2-е изд., испр.- М.: ИНФРА-М, 2010.
3. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч.1. М.: ОНИКС: Мир и Образование, 2009.
4. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч.2. М.: ОНИКС: Мир и Образование, 2009.
б) дополнительная литература:
1. Натансон И.П. Краткий курс высшей математики: учебник для студентов ВУЗов. СПб: Лань, 2008.
2. М.С.Красс. Математика для экономистов: учебное пособие для студентов высших учебных заведений. М: Питер, 2008.
3. Минорский В.П. Сборник задач по высшей математике. М.: Издательство Физико-математической литературы, 2008.
4. Высшая математика для экономистов: Учебник для студентов высших учебных заведений. / Под. ред. Н.Ш. Кремера. М.: ЮНИТИ, 2010.
5. Пискунов Н.С. Дифференциальное и интегральное исчисления: Учеб. пособие для втузов: В 2-х т. – М.: Интеграл-пресс, 2009.
6. Солодовников А.С. и др. Математика в экономике: Учебник для экон. спец. втузов: В 2-х ч. – М.: Финансы и статистика,2010.
Содержание
1. Общие рекомендации студенту-заочнику по работе над курсом
математики ……………………………………………………….…….…1- 3
2. Программа дисциплины ………………………………………………….4
3. Задачи для контрольных работ ………………………………………… 5 -11
4. Вопросы для самопроверки……………………………………………....12 -15
5. Литература………………………………………………………………………………16
ГОУ ВПО
«Сургутский государственный университет
Ханты-Мансийского автономного округа-Югра»
И.В.Шапошникова
МАТЕМАТИЧЕСКИЙ АНАЛИЗ
Часть 1
И.В.Шапошникова
Математический анализ. Часть 1: Учебно-методическое пособие для студентов заочной формы обучения спец. 080109 «Бухгалтерский учёт, анализ и аудит». -
Учебно-методическое пособие предназначено для студентов первого курса заочного факультета спец. 080109 «Бухгалтерский учёт, анализ и аудит» и содержит программу курса математического анализа, утверждённую методическим Советом университета, общие рекомендации студенту-заочнику по изучению данной дисциплины, список литературы, контрольные задания (10 вариантов) и вопросы для самопроверки по разделам курса Поскольку издание преследует сугубо учебно-методические цели, то оно носит компилятивный характер.
ОБЩИЕ РЕКОМЕНДАЦИИ СТУДЕНТУ-ЗАОЧНИКУ ПО РАБОТЕ НАД КУРСОМ ВЫСШЕЙ МАТЕМАТИКИ.
Основной формой обучения студента-заочника является самостоятельная работа над учебным материалом, которая состоит из изучения материала по учебникам, решения задач, выполнения контрольных работ, ответов на вопросы для самопроверки. В помощь студентам-заочникам кафедра высшей математики СурГУ организует чтение обзорных лекций, консультации в течение семестра и перед экзаменом (зачетом). Кроме того, студент может обращаться к преподавателю с вопросами в письменном или устном виде. Указания студенту по текущей работе даются также в процессе рецензирования контрольных работ. Однако студент должен помнить, что только при систематической и упорной самостоятельной работе помощь кафедры окажется достаточно эффективной.
Завершающим этапом изучения отдельных частей курса математического анализа является сдача экзаменов и зачетов в соответствии с учебным планом.
КОНТРОЛЬНЫЕ РАБОТЫ.
В процессе изучения курса математического анализа студент должен выполнить ряд контрольных работ, главная цель которых – оказать студенту помощь в его работе. Рецензии преподавателя позволяют студенту судить о степени усвоения им соответствующего раздела курса, указывают на имеющиеся у него пробелы. При выполнении контрольных работ студент должен руководствоваться следующими указаниями:
1. Не следует приступать к выполнению контрольного задания, не решив достаточного количества задач по материалу, соответствующему этому заданию. Опыт показывает, что затруднение при решении той или иной задачи контрольного задания вызвано тем, что студент не выполнил этого требования.
2. Каждую контрольную работу следует выполнять в отдельной тетради. Желательно оставлять на каждой странице широкие поля для замечаний рецензента.
3. На обложке тетради должны быть указаны фамилия и инициалы студента, учебный номер (шифр), название дисциплины, номер контрольной работы. В конце работы должны стоять дата её выполнения и подпись студента.
4. В работу должны быть включены все задачи, указанные в задании, строго по положенному варианту. Желательно оставлять на каждой странице широкие поля для замечаний рецензента.
5. Решения задач надо располагать в порядке возрастания их номеров, указанных в заданиях, сохраняя номер задачи. Перед решением задачи надо полностью выписать её условие.
6. Все вычисления должны быть приведены полностью, со ссылками на используемые формулы. Чертежи и графики должны быть выполнены аккуратно, четко, с указанием единиц масштаба и координатных осей.
7. После получения прорецензированной работы студент должен исправить в ней все ошибки. В случае незачета студент обязан в кратчайший срок выполнить все требования рецензента и предоставить исправленную работу на повторное рецензирование (исправления и дополнения к первоначальной работе обязательно выполняются в той же тетради). При отсутствии зачтенных контрольных работ студент не допускается к сессии.
8. Контрольная работа должна выполняться самостоятельно.
9. По учебному плану в первом семестре студент-заочник обязан выполнить три контрольные работы по математике согласно варианту номер которого совпадает с последней цифрой его учебного номера (шифра) (см. табл. 1).
Таблица 1
Распределение заданий по вариантам.
| Вариант | Номера задач контрольных заданий | |
| Контрольная работа № 1 | Контрольная работа № 2 | |
| 1,11,21 | 31,41,51,61, 71,81,91 | |
| 2,12,22 | 32,42,52,62, 72,82,92 | |
| 3,13,23 | 33,43,53,63, 73,83,93 | |
| 4,14,24 | 34,44,54,64, 74,84,94 | |
| 5,15,25 | 35,45,55,65, 75,85,95 | |
| 6,16,26 | 36,46,56,66, 76,86,96 | |
| 7,17,27 | 37,47,57,67, 77,87,97 | |
| 8,18,28 | 38,48,58,68, 78,88,98 | |
| 9,19,29 | 39,49,59,69, 79,89,99 | |
| 10,20,30 | 40,50,60,70, 80,90,100 |
ЗАЧЕТЫ И ЭКЗАМЕНЫ
После каждого семестра студент должен сдавать зачет или экзамен. Обычно экзамену или зачету предшествует собеседование студента с преподавателем по выполненным контрольным работам.
На зачете и экзамене от студента требуется знание определений, формулировок и доказательств теорем в объеме программы курса, знание формул и умение решать соответствующие задачи. При подготовке к экзамену рекомендуется повторить учебный материал по учебнику и конспекту.
ПРОГРАММА ДИСЦИПЛИНЫ “МАТЕМАТИЧЕСКИЙ АНАЛИЗ” (ЧАСТЬ I).
