Симметричный для x обозначим через x'.

Теорема 4.Пусть на множестве X задана ассоциативная операция °. Элементы x,yÎX — симметризуемы, тогда элемент x°y также симметризуем и симметричный для него (x°y)'= y'° x'.

Доказательство. Рассмотрим композицию: (x°y)°( y'° x')=x°(y°y') °x'=x°x'=n, где n – нейтральный элемент. Аналогично (y'°x') ° (x°y)=n.

Определение 6.Операция ° называется коммутативной, если x°y=y°x "x,yÎX.

Часто бинарную алгебраическую операцию называют сложением или умножением (так сложилось исторически), то композицию называют соответственно суммой или произведением.

Упражнение 1. Привести примеры.

Упражнение 2. Как называют нейтральный и симметричный элементы, если операцию называют сложением (умножением).

Определение группы. Простейшие свойства групп.

Определение1. Пусть Г не пустое множество элементов произвольной природы. Г называется группой, если выполняются следующие условия:

1) На множестве Г задана операция °.

2) Операция ° ассоциативна.

3) Существует нейтральный элемент nÎГ.

4) Для любого элемента из Г симметричный ему элемент всегда существует и принадлежит также Г.

Пример.

Множество Z – чисел с операцией +.

Определение 2.

Группа называется абелевой, если она коммутативна относительно заданной операции °.

Важные примеры групп

1) GL(n,P) — полная линейная группа над полем P степени n. Рассмотрим множество матриц порядка n над некоторым полем P, определитель которых отличен от нуля: GL(n,P)={A P_n , |A|¹0}. Проверим, что это группа:

1. Операция ° задана, ибо произведение невырожденных матриц — невырожденная матрица;

2. Операция ° ассоциативна, ибо произведение матриц ассоциативно;

3. Существует нейтральный элемент — единичная матрица;

4. Обратная матрица существует и принадлежит GL(n,P), а это и есть симметричный элемент.

2) SL(n,P)={AÎP_n , |A|=1} — специальная линейная группа степени n над полем. Это множество матриц над полем P порядка n, с определителем равным 1.

1. Операция ° задана, ибо |AB| = |A||B|=1;

2. Операция ° ассоциативна;

3. Существует нейтральный элемент — единичная матрица, ибо |E|=1;

4. Существует элемент симметричный — обратная матрица, так как определитель не равен нулю, и она принадлежит SL(n,P).

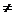3) S(X) — симметричная группа на множестве X, где X — не пустое множество, S(X) — множество биективных отображений из X в X. Тождественное отображение принадлежит , следовательно, S(X) Æ

1. Операция ° задана, ибо произведение биективных отображений — биективное отображение;

2. Операция ° ассоциативна, ибо произведение отображений ассоциативно;

3. Существует нейтральный элемент e_x (тождественное отображение на X);

4. Существует обратное отображение, для любого биективного отображения и оно принадлежит S(X).

Если X — конечное множество и состоит из n элементов |C|=n, то в этом случае S(X) обозначается S_n , так как природа элементов не существенна, то полагаем Х={1,…,n}.

4) Рассмотрим множество четных подстановок A_n на множестве из n элементов. A_n ¹Æ, ибо тождественное отображение принадлежит A_n.

1. Операция ° задана (произведение четных подстановок— четная подстановка);

2. Операция ° – ассоциативна;

3. Тождественная подстановка играет роль единицы;

4. Для любой подстановки из A_n существует обратная подстановка (она тоже четная).

A_n — знакопеременная группа степени n.

Простейшие свойства групп

1) В группе существует единственный нейтральный элемент (существует по определению, по теореме 1 из §1 единственный);

2) в группе для каждого элемента существует единственный симметричный ему элемент(существует по определению, по теореме 3 из § 1 единственный);

3) Пусть Г — группа с операцией °, тогда уравнения вида :

a°x=b и x°a=b (1) — разрешимы и имеют единственное решение.

Доказательство. Рассмотрим уравнения (1) относительно x. Очевидно, что для а $! а'. Так как операция ° — ассоциативна, то очевидно x=b°a' — единственное решение.

Подгруппа

Определение.Пусть Г — группа c операцией ° и не пустое подмножество HÌГ, тогда H называют подгруппой группы Г, если H —группа относительно индуцированной операции °,т.е. выполняются условия:

1) H устойчиво относительно индуцированной операции °;

2) В H должен быть нейтральный элемент относительно индуцированной операции °;

3) В H должен быть симметричный элемент относительно индуцированной операции ° для любого hÎH.

Запись H £ Г означает, что H — подгруппа группы Г.

Примеры.

1) Г = (Z,+), H = {2Z,+}В этом случае обозначается H<Г.

2) SL(n,P) < GL(n,P).

Теорема (критерий подгруппы).Пусть Г — группа относительно операции°, ƹH Г. H является подгруппой тогда и только тогда, когда "h₁,h₂ H выполняется условие h₁°h₂' H (где h₂' — симметричный элемент к h₂).

Доказательство. Необходимость: Пусть H — подгруппа (нужно доказать, что h₁°h₂' H). Возьмем h₁,h₂ H, тогда h₂' H и h₁°h'₂ H (так как h'₂ — симметричный элемент к h₂).

Достаточность: (надо доказать, что H — подгруппа).

Раз H¹Æ , то там есть хотя бы один элемент. Возьмем h H, n=h°h' H, т.е. нейтральный элемент n 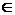H. В качестве h₁ берем n, а в качестве h₂ возьмём h тогда h' H Þ " h H симметричный элемент к h также принадлежит H.

Докажем, что композиция любых элементов из Н принадлежит Н.

Возьмём h₁ , а в качестве h₂ возьмём h'₂ Þ h₁°(h₂') ' H, Þ h₁°h₂ H.

Пример.

Г=S_n, n>2, α — некоторый элемент из Х={1,…,n}. В качестве H возьмём не пустое множество H= S^α_n ={f S_n ,f(α)=α}, при действии отображения из S _n α остаётся на месте. Проверяем по критерию. Возьмём любые h₁,h₂ H. Произведение h₁^.h₂' H, т.е H — подгруппа, которая называется стационарной подгруппой элемента α.

Кольцо.

Определение.Пусть К непустое множество с двумя алгебраическими операциями: сложением и умножением. Кназывается кольцом, если выполняются следующие условия:

1)К—абелевагруппа относительно сложения;

2) умножение ассоциативно;

3)умножение дистрибутивно относительно сложения.

Если умножение коммутативно, то К называют коммутативным кольцом. Если относительно умножения есть нейтральный элемент, то К называют кольцом с единицей.

Примеры.

1) Z,+,´ — коммутативное кольцо с единицей.

2) 2Z,+,´ — коммутативное кольцо без единицы.

3) P_n ,+, ´ — не коммутативное кольцо с единицей.

Простейшие свойства колец.

1. Так как К абелева группа относительно сложения, то на К переносятся простейшие свойства групп.

2. Умножение дистрибутивно относительно разности:

a(b-c)=ab-ac.

Доказательство. Т.к. ab-ac+ac=ab и a(b-c)+ac=a((b-c)+c)=a(b-c+c)=ab, то a(b-c)=ab-ac.

3. В кольце могут быть делители нуля, т.е. ab=0, но отсюда не следует, что a=0 b=0.

Например, в кольце матриц размера 2´2, существуют элементы не равные нулю такие, что их произведение будет нуль:

,где — играет роль нулевого элемента.

4. a·0=0·а=0.

Доказательство. Пусть 0=b-b. Тогда a(b-b)=ab-ab=0. Аналогично 0·а=0.

5. a(-b)=(-a)·b=-ab.

Доказательство: a(-b)+ab=a((-b)+b)=a·0=0.

6. Если в кольце К существует единица и оно состоит более, чем из одного элемента, то единица не равна нулю, где 1─ нейтральный элемент при умножении; 0 ─ нейтральный элемент при сложении .

Доказательство (от противного). Предположим противное. Пусть 1=0. Возьмем " aÎК, тогда a=a*1=a*0=0Þa=0. Значит кольцо состоит из одного элемента. Противоречие с условием теоремы, ибо,|K|≥2.

7. Пусть К кольцо с единицей, тогда множество обратимых элементов кольца образуют группу относительно умножения, которую называют мультипликативной группой кольца K и обозначают K*.

Доказательство.

К^*¹Æ. Пусть aÎ K* и bÎ K*. Докажем, что abÎ K*. В самом деле

(ab)^-1=b^-1a^-1 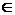K^*, ибо a^-1,b^-1 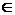K^*.

§5. Поле

Определение. Коммутативное кольцо с единицей, содержащее не менее двух элементов, в котором любой отличный от нуля элемент обратим, называется полем.

Простейшие свойства поля

1. Т.к. поле — кольцо, то все свойства колец переносятся и на поле.

2. В поле нет делителей нуля ,т.е. если ab=0 ,то a=0 или b=0.

Доказательство.

Если a¹0 ,то $ a^-1 . Рассмотрим a^-1 (ab)=( a^-1 a)b=0 , а если a¹0 ,то b=0, аналогично если b¹0

3. Уравнение вида a´x=b, a¹0, b – любое, в поле имеет единственное решение x= a^-1b, или х=b/a.

Решение этого уравнения называется частным.

Примеры.

1)PÌC, P — числовое поле.

2)P={0;1};

3) P={0;1;2} .

Характеристика поля

Не все свойства числовых полей сохраняются в случае произвольного поля. Так, складывая число 1 само с собою несколько раз, т.е. беря любое целое положительное кратное единицы, мы никогда не получим нуля. Если же мы будем брать целые кратные единицы в каком-либо конечном поле, то среди них непременно будут равные, т.к. это поле обладает лишь конечным числом различных элементов. Если все целые кратные единицы поля P являются различными элементами поля P, т.е. k°1¹m°1(здесь и далее за 1 обозначен элемент поля = единице) при k¹m, то говорят, что поле P имеет характеристику нуль(char P=0);таковы, например, все числовые поля. Если существуют такие целые k и m, что k>m, но в P имеет место равенство k°1=m°1, то (k-m) °1=0, т.е. в P существует такое положительное кратное единицы, которое оказывается равным нулю. В этом случае P называется полем положительной характеристики. Характеристикой поля в случае поля положительной характеристики называют наименьшее натуральное р, что единица сложенная р раз дает 0.

Cвойства характеристики

1) Если char P=p>0, то p — простое число.

Доказательство (от противного).

Пусть p не простое число, а составное, т.е. p=n°s, n>1,s>1 . Сложим единицу p раз: p°1=(n°1)·( s°1)=0 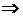n○1=0 либо s○1=0. Ибо в поле нет делителей нуля, но n<p и s<p. Противоречие с выбором числа p.

2) a°p =0, " aÎP .

Любой элемент поля, сложенный р раз, где p — характеристика, равен нулю.

Доказательство:

a°p= =a° = a(p°1)=a×0=0