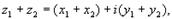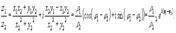Теорема. Любые два n-мерных линейных пространства изоморфны.

Это означает, что все 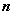-мерные линейные пространства “устроены” одинаково — как пространство 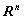векторов-столбцов из 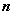действительных чисел, т.е. что все они изоморфны пространству .

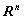Изоморфизм 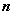-мерных линейных пространств пространству 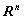означает, что соотношения между элементами 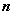-мерного линейного пространства и операции с ними можно изучать как соотношения между векторами из 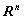и операции с ними и что всякое утверждение относительно векторов из 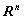справедливо для соответствующих элементов любого 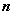-мерного линейного пространства.

Свойства линейных пространств.

1) В каждом линейном пространстве существует только один нулевой элемент.

2) Для каждого элемента существует только один противоположный элемент.

3) Для каждого Î L верно 0× = 0

4) Для каждого a Î R и 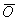Î L верно a× =

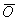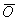
5) Если a× = 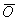, то a = 0 или =

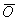
6) (-1) = -

Линейные преобразования.

Определение: Будем считать, что в линейном пространстве L задано некоторое линейное преобразование А, если любому элементу Î L по некоторому правилу ставится в соответствие элемент А Î L.

Определение: Преобразование А называется линейным, если для любых векторов Î L и 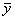Î L и любого a верно:

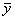A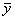( + ) = A +A

A(a ) = aA

Определение: Линейное преобразование называется тождественным, если оно преобразует элемент линейного пространства сам в себя.

Е =

Пример. Является ли А линейным преобразованием. А = + 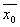; 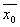¹ 0.

Запишем преобразование А для какого- либо элемент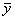а . А = +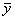

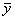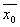
Проверим, выполняется ли правило операции сложения для этого преобразования А( + 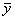) = 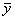+ + 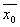; A( ) + A( 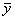) = + + 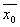+ 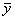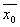, что верно только при 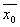= 0, т.е. данное преобразование А нелинейное.

Определение: Если в пространстве L имеются векторы линейного преобразования 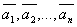, то другой вектор 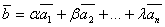является линейной комбинацией векторов .

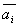Определение: Если 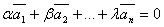только при a = b = … = l = 0, то векторы 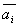называются линейно независимыми.

Определение: Если в линейном пространстве L есть n линейно независимых векторов, но любые n + 1 векторов линейно зависимы, то пространство L называется n-мерным, а совокупность линейно независимых векторов называется базисом линейного пространства L.

Следствие: Любой вектор линейного пространства может быть представлен в виде линейной комбинации векторов базиса.

Матрицы линейных преобразований.

Пусть в n- мерном линейном пространстве с базисом 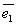, ,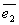…, 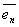задано линейное преобразование А. Тогда векторы 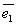А 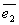,А ,…,А 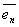- также векторы этого пространства и их можно представить в виде линейной комбинации векторов базиса:

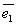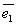A = a₁₁ + a₂₁ 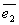+…+ a_n1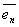

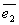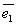A = a₁₂ + a₂₂ 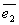+…+ a_n2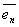

……………………………….

A 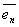= a_n1 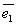+ a_n2 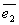+…+ a_nn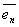

Тогда матрица А = называется матрицей линейного преобразования А.

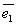Если в пространстве L взять вектор = x₁ + x₂ 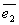+…+ x_n 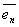, то A Î L.

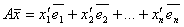_{, где}

……………………………..

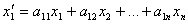
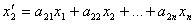
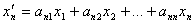
Эти равенства можно назвать линейным преобразованием в базисе , ,…, .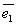

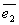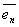В матричном виде:

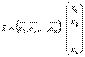_{, А× , 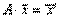Пример. Найти матрицу линейного преобразования, заданного в виде:}

x¢ = x + y

y¢ = y + z

z¢ = z + x

x¢ = 1×x + 1×y + 0×z

y¢ = 0×x + 1×y + 1×z

z¢ = 1×x + 0×y + 1×z

A =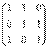

На практике действия над линейными преобразованиями сводятся к действиям над их матрицами.

Определение: Если вектор переводится в вектор 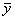линейным преобразованием с матрицей А, а вектор 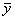в вектор 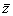линейным преобразованием с матрицей В, то последовательное применение этих преобразований равносильно линейному преобразованию, переводящему вектор в вектор 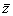(оно называется произведением составляющих преобразований).

С = В×А

Пример. Задано линейное преобразование А, переводящее вектор в вектор 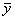и линейное преобразование В, переводящее вектор 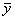в вектор 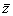. Найти матрицу линейного преобразования, переводящего вектор в вектор .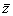

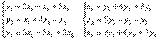
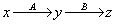
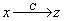
С = В×А

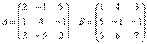
Т.е.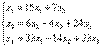

Примечание: Если ïАï= 0, то преобразование вырожденное, т.е., например, плоскость преобразуется не в целую плоскость, а в прямую.

Комплексным числомz называется упорядоченная пара действительных чисел x и y.
Первое из них x называется действительной частью комплексного числа z и обозначается Rez, x = Rez;
второе число y называется мнимой частью комплексного числа z и обозначается Imz, y = Imz.
Два комплексных числа равны тогда и только тогда, когда равны их действительные и мнимые части:

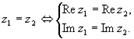
Алгебраическая форма записи комплексного числа

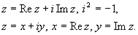
Число
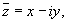
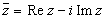, где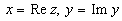
называется комплексно сопряженным числу

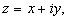
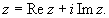
Комплексное число z = x + iy естественно изображать в виде точки на плоскости с декартовыми координатами (x, y).

Если x и y - декартовы координаты точки плоскости, то, перейдя на плоскости к полярным координатам (r, j) и воспользовавшись связью
x = rcosj, y = rsinj
получим тригонометрическую форму записи комплексного числа:
z = r (cosj + isinj) .
При этом число r называют модулем комплексного числа, |z| = r, а число j - аргументом комплексного числа,
Arg z = arg z+2kp= j.

При решении задач для вычисления аргумента удобно пользовааться схемой, приведенной ниже:

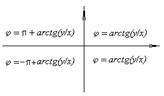
Справедливы соотношения:

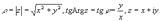
Используя формулу Эйлера

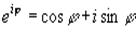
получим показательную форму записи комплексного числа:

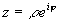
Арифметические операции c комплексными числами определяются следующим образом:
если

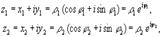
то