Метод координат на плоскости и в пространстве
Систему координат будем вводить параллельно на плоскости и в пространстве.
На плоскости Определение 17. Аффинным репером называется совокупность фиксированной точки и фиксированного базиса, т.е. R = 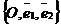 . Точка О называется началом координат, векторы . Точка О называется началом координат, векторы 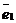 и и 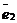 - координатными векторами. Точка О вместе с каждым координатным вектором определяет ось. Эти оси называются координатными осями и обозначаются (Ох) и (Оу) (рис. 20). - координатными векторами. Точка О вместе с каждым координатным вектором определяет ось. Эти оси называются координатными осями и обозначаются (Ох) и (Оу) (рис. 20). 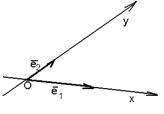 Рис. 20 Координатные оси разбивают плоскость на четыре угла. Их называют координатными углами. Координатные углы нумеруются в направлении кратчайшего поворота оси (Ох) к оси (Оу). Говорят, что репер R = Рис. 20 Координатные оси разбивают плоскость на четыре угла. Их называют координатными углами. Координатные углы нумеруются в направлении кратчайшего поворота оси (Ох) к оси (Оу). Говорят, что репер R = 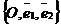 задаёт на плоскости систему аффинных координат. Пусть М – произвольная точка плоскости. Вектор задаёт на плоскости систему аффинных координат. Пусть М – произвольная точка плоскости. Вектор 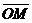 (рис. 21) называется радиусом- -вектором точки М (его часто обозначают одной буквой (рис. 21) называется радиусом- -вектором точки М (его часто обозначают одной буквой  ). ). 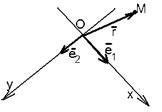 Рис. 21 Между множеством всех точек плоскости и множеством всех компланарных векторов, которые можно отложить в этой плоскости, устанавливается взаимнооднозначное соответствие. Следовательно, радиус-вектор точки вполне определяет эту точку и называется её векторной координатой. Обозначение М( Рис. 21 Между множеством всех точек плоскости и множеством всех компланарных векторов, которые можно отложить в этой плоскости, устанавливается взаимнооднозначное соответствие. Следовательно, радиус-вектор точки вполне определяет эту точку и называется её векторной координатой. Обозначение М( 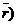 . В базисе . В базисе 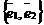 , входящем в данный репер, вектор , входящем в данный репер, вектор 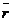 задаётся упорядоченной парой своих координат. Между множеством всех компланарных векторов и множеством всех упорядоченных пар действительных чисел тоже устанавливается взаимно однозначное соответствие. Итак, М « задаётся упорядоченной парой своих координат. Между множеством всех компланарных векторов и множеством всех упорядоченных пар действительных чисел тоже устанавливается взаимно однозначное соответствие. Итак, М « 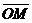 « {x, y}. Отсюда следует, что между множеством всех точек плоскости и множеством всех упорядоченных пар действительных чисел устанавливается взаимнооднозначное соответствие. Следовательно, любая точка плоскости вполне определяется упорядоченной парой действительных чисел. Определение 18. Аффинными координатами точки в репере R = « {x, y}. Отсюда следует, что между множеством всех точек плоскости и множеством всех упорядоченных пар действительных чисел устанавливается взаимнооднозначное соответствие. Следовательно, любая точка плоскости вполне определяется упорядоченной парой действительных чисел. Определение 18. Аффинными координатами точки в репере R = 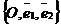 называются координаты её радиуса-вектора в базисе, входящем в этот репер. М(х, у)R Û называются координаты её радиуса-вектора в базисе, входящем в этот репер. М(х, у)R Û 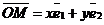 . Замечание. Если зафиксирован только один репер, то координаты точки можно обозначать М(х, у). . Замечание. Если зафиксирован только один репер, то координаты точки можно обозначать М(х, у). | В пространстве Определение 171. Аффинным репером называется совокупность фиксированной точки и фиксированного базиса, т.е. R = 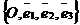 . Точка О называется началом координат, векторы . Точка О называется началом координат, векторы 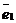 , , 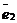 и и 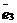 -координатными векторами. Точка О вместе с каждым координатным вектором определяет ось. Эти оси называются координатными осями и обозначаются (Ох), (Оу) и (Оz) (рис. 201). -координатными векторами. Точка О вместе с каждым координатным вектором определяет ось. Эти оси называются координатными осями и обозначаются (Ох), (Оу) и (Оz) (рис. 201). 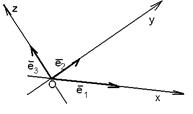 Рис. 201 Каждая пара координатных осей определяет плоскость. Их называют координатными плоскостями и обозначают (ХОУ), (ХОZ) и (УОZ). Координатные плоскости разбивают пространство на 8 трёхгранных углов. Их называют координатными углами. Говорят, что репер R = Рис. 201 Каждая пара координатных осей определяет плоскость. Их называют координатными плоскостями и обозначают (ХОУ), (ХОZ) и (УОZ). Координатные плоскости разбивают пространство на 8 трёхгранных углов. Их называют координатными углами. Говорят, что репер R = 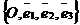 задаёт в пространстве систему аффинных координат. Пусть М – произвольная точка пространства. Вектор задаёт в пространстве систему аффинных координат. Пусть М – произвольная точка пространства. Вектор 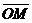 (рис.211) называется радиусом-вектором точки М (его часто обозначают одной буквой (рис.211) называется радиусом-вектором точки М (его часто обозначают одной буквой 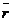 ). ). 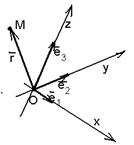 Рис.211 Между множеством всех точек плоскости и множеством всех геометрических векторов устанавливается взаимнооднозначное соответствие. Следовательно, радиус-вектор точки вполне определяет эту точку и называется её векторной координатой. Обозначение М( Рис.211 Между множеством всех точек плоскости и множеством всех геометрических векторов устанавливается взаимнооднозначное соответствие. Следовательно, радиус-вектор точки вполне определяет эту точку и называется её векторной координатой. Обозначение М( 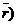 . В базисе . В базисе 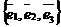 , входящем в данный репер, вектор , входящем в данный репер, вектор 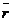 задаётся упорядоченной тройкой своих координат. Между множеством всех геометрических векторов и множеством всех упорядоченных троек действительных чисел тоже устанавливается взаимно однозначное соответствие. Итак, М « задаётся упорядоченной тройкой своих координат. Между множеством всех геометрических векторов и множеством всех упорядоченных троек действительных чисел тоже устанавливается взаимно однозначное соответствие. Итак, М « 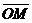 « {x, y, z}. Отсюда следует, что между множеством всех точек пространства и множеством всех упорядоченных троек действительных чисел устанавливается взаимнооднозначное соответствие. Следовательно, любая точка пространства вполне определяется упорядоченной тройкой действительных чисел. Определение 18. Аффинными координатами точки в репере R = « {x, y, z}. Отсюда следует, что между множеством всех точек пространства и множеством всех упорядоченных троек действительных чисел устанавливается взаимнооднозначное соответствие. Следовательно, любая точка пространства вполне определяется упорядоченной тройкой действительных чисел. Определение 18. Аффинными координатами точки в репере R = 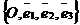 называются координаты её радиуса-вектора в базисе, входящем в этот репер. М(х, у, z)R Û называются координаты её радиуса-вектора в базисе, входящем в этот репер. М(х, у, z)R Û 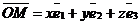 . Замечание. Если зафиксирован только один репер, то координаты точки можно обозначать М(х, у, z). . Замечание. Если зафиксирован только один репер, то координаты точки можно обозначать М(х, у, z). |
Итак, введение аффинных координат позволяет каждую точку плоскости (пространства) характеризовать парой (тройкой) действительных чисел, т.е. перейти с геометрического языка на язык алгебры. Частным случаем аффинной системы координат является прямоугольная система координат.
Определение 19. Ортонормированным репером называется совокупность фиксированной точки и фиксированного ортонормированного базиса, т.е. 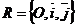 на плоскости ( и
на плоскости ( и 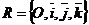 в пространстве). Аффинная система координат (АСК), которая задаётся ортонормированным репером, называется прямоугольной декартовой системой координат (ПДСК).
в пространстве). Аффинная система координат (АСК), которая задаётся ортонормированным репером, называется прямоугольной декартовой системой координат (ПДСК).
Аффинные задачи.
1. Координаты вектора, заданного координатами его концов.
На плоскости Дано: R = 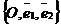 , А(х1, у1), В(х2, у2). Найти координаты вектора , А(х1, у1), В(х2, у2). Найти координаты вектора 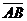 (рис.19). (рис.19). 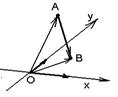 Рис. 22 Решение. А(х1, у1) Þ Рис. 22 Решение. А(х1, у1) Þ 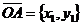 , В(х2, у2) Þ , В(х2, у2) Þ 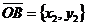 . Так как . Так как 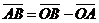 , то , то 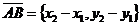 . . | В пространстве Дано: R = 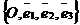 , А(х1, у1, z1), В(х2, у2, z2). Найти координаты вектора , А(х1, у1, z1), В(х2, у2, z2). Найти координаты вектора 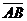 (рис. 191). (рис. 191). 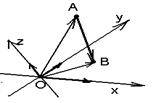 Рис. 221 Решение. А(х1, у1, z1) Þ Рис. 221 Решение. А(х1, у1, z1) Þ 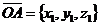 , В(х2, у2, z2) Þ , В(х2, у2, z2) Þ 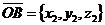 . Так как . Так как 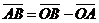 , то , то 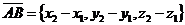 . . |
2. Координаты точки, делящей отрезок в данном отношении.
Зная координаты двух точек А и В, найти координаты такой точки С, что 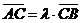 (*).
(*).
Замечание. Из условия (*) следует, что точки А, В, С лежат на одной прямой. Если l > 0, то точка С лежит между точками А и В. Если l < 0, но ½l½> 1, то точка С лежит вне отрезка АВ
| со стороны точки В. Если l < 0, но ½l½< 1, то точка С лежит вне отрезка АВ со стороны точки А. Если l = 1, то С – середина отрезка АВ. Очевидно, всегда l ¹ - 1. |  |
Решение. Приведём решение в случае плоскости. В случае пространства решение проведите самостоятельно.
Пусть С(х, у, z). Тогда 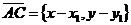 ,
, 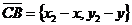 . Перепишем равенство (*) в координатах. Получим х - х1 = l(х2- х), у - у1 = l(у2 - у). Отсюда
. Перепишем равенство (*) в координатах. Получим х - х1 = l(х2- х), у - у1 = l(у2 - у). Отсюда 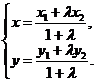
Метрические задачи.
Замечание. Метрические задачи можно решать в любой АСК, но рациональные вычислительные формулы получаются в ПДСК.
1. Расстояние между точками.
На плоскости Дано: 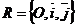 , А(х1, у1), В(х2, у2). Найти ½АВ½. Решение. ½АВ½ = , А(х1, у1), В(х2, у2). Найти ½АВ½. Решение. ½АВ½ =  . Так как . Так как 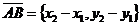 и базис и базис  ортонормированный, то ортонормированный, то 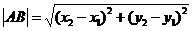 . . | В пространстве Дано: 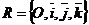 , А(х1, у1, z1), В(х2, у2, z2). Найти ½АВ½. Решение. ½АВ½ = , А(х1, у1, z1), В(х2, у2, z2). Найти ½АВ½. Решение. ½АВ½ = 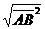 . Так как . Так как 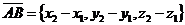 и базис и базис 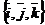 ортонормированный, то ортонормированный, то 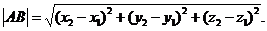 . . |
2. Угол, заданный тремя точками.
Приведём решение этой задачи в случае пространства. Для плоскости решение проведите самостоятельно.
Дано: 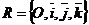 , А(х1, у1, z1), В(х2, у2, z2), С(х3, у3, z3). Найти ÐВАС. Решение. , А(х1, у1, z1), В(х2, у2, z2), С(х3, у3, z3). Найти ÐВАС. Решение. 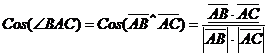 . Перепишем в координатах: . Перепишем в координатах: 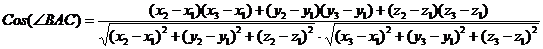 |
