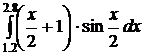Вычисление интеграла по методу Симпсона

Метод Симпсона применяется для вычисления определенных интегралов вида .

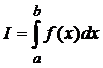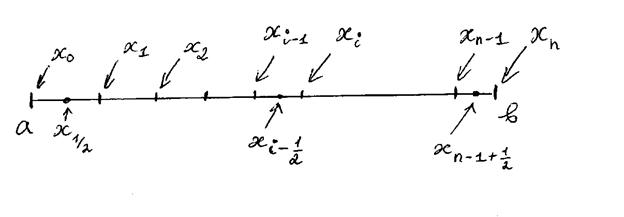
Разобьем отрезок [a, b] на n точек.

Представим искомый интеграл в виде суммы интегралов:

,

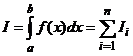здесь

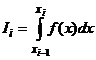
Рассмотрим i-ый отрезок [x_i-1, x_i]

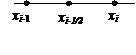x_i-1/2=(x_i+x_i-1)/2 – середина i-го отрезка

Представим на отрезке [x_i-1, x_i] подынтегральную функцию f(x) в виде полинома третьей степени P_i(x). Этот полином должен быть равен значениям подынтегральной функции в точках сетки и в середине отрезка: P_i(x_i-1)=f(x_i-1)– равенство полинома значению функции на левой границе i-го отрезка,

P_i(x _i-1/2) = f(x_i-1/2), P_i(x _i) = f(x_i).

Такой полином можно записать, например, следующим образом:

P_i(x)=a+b(x-x_i-1)+c(x-x_i-1)(x-x_i-1/2),

здесь a, b, c – неизвестные коэффициенты, подлежащие определению.

Введем обозначение для ширины i-го отрезка: h_i=x_i-x_i-1,

тогда (x-x_i-1/2)= h_i/2, а (x_i-1/2-x _i-1)= h_i/2.

Запишем значения полинома на левой, правой границах и в середине i-го отрезка

P_i(x _i) = a+b*h_i+c*h_i*h_i/2 = f(x _i)= f_i (1)

P_i(x _i-1) = a = f(x _i-1)= f_i-1 (2)

P_i(x _i-1/2)= f(x _i-1/2)= a+b*h_i/2 = f_i-1/2 (3)

Из соотношения (2) следует a= f_i-1,

из выражения (3) легко увидеть, что b= h_i (f_i-1/2 - f_i)/2,

из выражения (1) получаем c=2 (f_i-a-b h_i)/h_i², подставим в выражение для коэффициента c выражения для коэффициентов a и b, в результате получим:

c=2(f_i - f_i-1) /h_i² – (2/h_i)(2/h_i)(f_i-1/2- f_i-1),

c=2 [f_i - f_i-1-2 f_i-1/2+2 f_i-1] /h_i²,

c=2 [f_i -2 f_i-1/2+f_i-1] /h_i².

Подставим найденные коэффициенты a, b, c в выражение для полинома:

P_i(x )= f_i-1 + 2(f_i-1/2- f_i-1)( x -x _i-1) /h_i + 2 [f_i -2 f_i-1/2+f_i-1] ( x -x _i-1) ( x -x _i-1/2)/h_i²

Перейдем от переменной x к переменной t= x -x _i-1

Тогда dt = dx, а при x = x _i-1; t=0, при x = x _i; t=h_i при

x = x _i-1/2=x-( x_i -x _i-1)/2= x-x_i/2 -x _i-1/2= x- x _i-1+x _i-1/2-x_i/2=t-h_i/2

Тогда на i-ом интервале значение интеграла с учетом введенных обозначений, можно записать:

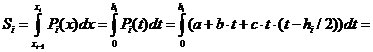
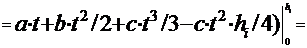
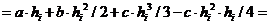
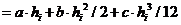
Подставим в выражение для 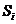значения коэффициентов a,b и c

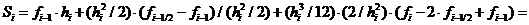
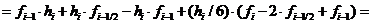
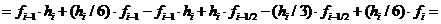
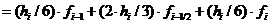
Таким образом,

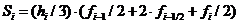
S_i – представляет собой значение интеграла на i-ом отрезке. Для получения интеграла на отрезке от a до b, необходимо сложить все S_i

Если h_i=h для любого i=1,…, N, тогда 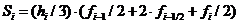и формулу Симпсона можно упростить

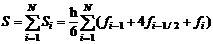(4)

Формулу (4) можно упростить, для этого раскроем скобки в выражении под знаком суммирования

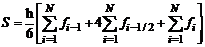
Выделим из первой суммы значение функции в точке x=a

,

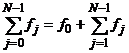а из последней суммы – значение функции в точке x=b

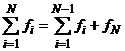
В результате получаем рабочую формулу Симпсона для равномерной сетки.

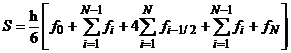
или

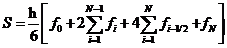
Учтем, что 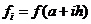, , 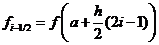получим окончательное выражение для формулы Симпсона

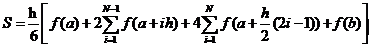(5)

В первой сумме формулы (5) вычисляют сумму значений функции во всех внутренних узлах отрезка [a, b], вторая сумма вычисляет сумму значений функции в средних точках i-ых отрезков.

Если середины отрезков включить в сетку наряду с узлами, тогда новый шаг h₀ = h/2 = (b-a)/(2*n), а формула (5) может быть записана в виде:

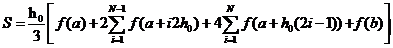(6)

Рассмотрим 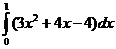. Значение данного интеграла легко найти аналитически и оно равно -0,75. Метод Симпсона для подынтегральной функции в виде полинома степени 3 и ниже дает точное значение.

Алгоритм вычисления этого интеграла методом Симпсона (формула (5)).

a=0

b=1

n=5

h=(b-a)/n

f0=f1(a)

fn=f1(b)

s1=0

x1=a+h

цикл по i от 1 до n-1

s1=s1+f1(x1)

x1=x1+h

конец цикла

x2=a+h/2

s2=0

цикл по I от 1 до n

s2=s2+f1(x2)

x2=x2+h

конец цикла

s=h*(f0+2*s1+4*s2+fn)/6

Печать s

функция f1

параметры x

возврат x^3+3*x^2 + x*4 - 4

Пример программы вычисления интеграла методом Симпсона на языке VFP(по формуле (6)):

CLEAR

SET DECIMALS TO 10

? "I=",simpson(0,2,20)

x=2

? "I=",x^3/3

PROCEDURE simpson

PARAMETERS a,b,n

h=(b-a)/n

S_четные=0

S_нечетные=0

for x=a+h TO b-h STEP 2*h

S_нечетны = S_нечетные + 4*f(x)

NEXT

for x=a+2*h TO b-h STEP 2*h

S_четные = S_четные + 2*f(x)

NEXT

S=f(a)*h/3+(S_четные+S_нечетные)*h/3+f(b)*h/3

RETURN s

FUNCTION f

PARAMETERS x

RETURN x^2

Пример решения на языке VBA:

'процедура проверки правильности вычисления значения интеграла по его первообразной

Sub s_test(x)

i = x ^ 3 / 3

End Sub

Function f(x)

f = x ^ 2

End Function

Sub simpson()

a = 0

b = 2

n = 30

x = 2

h = (b - a) / n

s_четные = 0

s_нечетные = 0

For x = a + h To b - h Step 2 * h

s_нечетные = s_нечетные + 4 * f(x)

Next

Debug.Print "s_нечетные = " & s_нечетные

For x = a + 2 * h To b - h Step 2 * h

s_четные = s_четные + 2 * f(x)

Next

Debug.Print "s_четные=" & s_четные

s = h / 3 * (f(a) + (s_четные + s_нечетные) + f(b))

Debug.Print "Метод Симпсона : s= " & s

Debug.Print "Значение первообразной : s_test= ” & s_test(b-a)

End Sub

Результат работы программы на VBA:

s_нечетные = 79,9111111111111

s_четные=36,0888888888889

Метод Симпсона : s= 2,66666666666667

Значение первообразной : s_test= 2,66666666666667

Контрольные вопросы

1. Что такое определенный интеграл?

2. Привести алгоритм метода прямоугольников.

3. На интервале [a,b] функция f(x) монотонно возрастает. I₁ – значение интеграла функции f(x) на отрезке [a,b], вычисленное по методу левых прямоугольников, I₀ – значение интеграла функции f(x) на отрезке [a,b], вычисленное по методу средних прямоугольников. Будут ли отличаться значения интеграла, вычисленные этими методами? Если значения различны, то какое из них больше? Чем определяется разница?

4. Оценить погрешность для вычисления интеграла методом правых прямоугольников для монотонно убывающей функции.

5. Привести алгоритм метода трапеций.

6. Привести алгоритм метода Симпсона.

7. Как определить погрешность вычисления интеграла итерационными методами?

8. Какой из методов имеет наименьшую погрешность вычисления определенного интеграла?

9. Получить формулу метода Симпсона.

Задания

Вычислить следующие интегралы методами: прямоугольников, трапеций, Симпсона с точностью 0,001 и оценить погрешность результатов вычислений этими методами.

1.

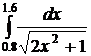
2.

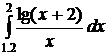
3.

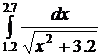
4.

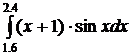
5.

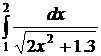
6.

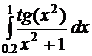
7.

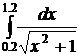
8.

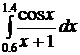
9.

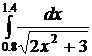
10.

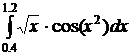
11.

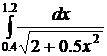
12.

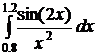
13.

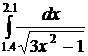
14.

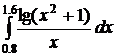
15.

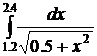
16.

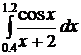
17.

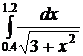
18.

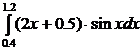
19.

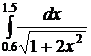
20.

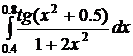
21.

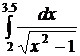
22.

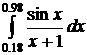
23.

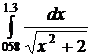
24.

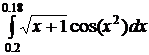
25.

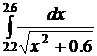
26.

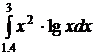
27.

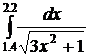
28.

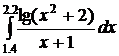
29.

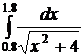
30.

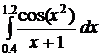
31.

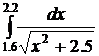
32.

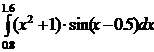
33.

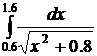
34.

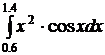
35.

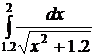
36.

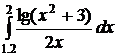
37.

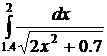
38.

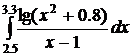
39.

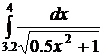
40.

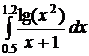
41. 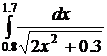42.

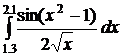
43.

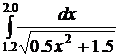
44.

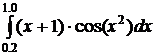
45.

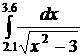
46.

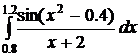
47.

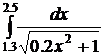
48.

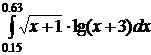
49.

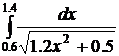
50.

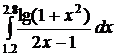
51.

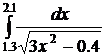
52.

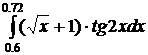
53.

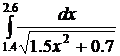
54.

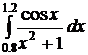
55.

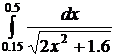
56.