Решение систем линейных уравнений методом Гаусса с выбором максимального элемента

Исходная матрица a_i,j может в общем случае иметь на диагонали нулевые элементы. Поэтому, для применения базовой процедуры приведения к треугольному виду (***), матрицу нужно преобразовать так, чтобы на диагонали стояли ненулевые элементы.

Так, для элемента a_1,1

находим в области i≥1, j≥1 максимальный по модулю элемент a(i_max, j_max) и совершаем перестановку строк:

i_max меняется с первой строкой местами, то есть строка с номером i_max становится первой строкой, а первая строка становится строкой с номером i_max.

Аналогичную перестановку делают для столбцов матрицы: столбец, содержащий максимальное значение, меняется со столбцом с первым номером.

При перестановке строк необходимо переставить и элементы вектора b:

x=b(j_max)

b(j_max)=b(1)

b(1)=1

При перестановке столбцов переставляются векторы решений:

x(j_max) x(1)

Эти перестановки необходимо запоминать, чтобы после получения вектора решений по треугольной матрице восстановить правильный порядок элементов x_i.

Введем вектора:

ni(n)=(1, 2, 3, …, n) – начальный порядок строк,

nj(n)=(1, 2, 3, …, n) начальный порядок столбцов.

j_max 1

nj(1)=j_max

nj(j_max)=1

Так, если j_max =4 до перестановки nj (1, 2, 3, 4, 5, 6), после перестановки nj (4, 2, 3, 1, 5, 6).

В алгебре используется понятие характеристической функции матрицы. Характеристическая функция F(C) для матрицы A получается следующим образом:

F(C) = Det |A-E*C|,

здесь Det|A-E*C| определитель разности матрицы A и единичной матрицы E умноженной на неизвестную переменную величину C – аргумент характеристической функции. Так, например, для матрицы

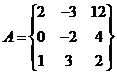
характеристическая функция записывается следующим образом:

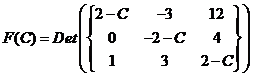
В данном случае, для матрицы 3x3 характеристическая функция представляет собой полином степени 3 и может иметь один или три действительных корня. Корни характеристического уравнения

F(C) = 0

могут быть найдены явно (в простых случаях) или численным образом при помощи методов табуляции, деления отрезка пополам, секущих и т.д. Корни характеристического уравнения называют собственными значениями соответствующей матрицы.

Пример программного кода метода Гаусса с выбором максимального элемента на языке VFP:

PROCEDURE гаусс

LPARAMETERS a2,b2,x,n

DIMENSION a2(n,n),b2(n),x(n)

LOCAL ARRAY x1(n),ix(i),a(n,n),b(n)

LOCAL i,j,k,l,m,im,jm,i1,j1,aa,s

* задаем рабочую матрицу и рабочие правые части

FOR i=1 TO n

b(i)=b2(i)

ENDFOR

FOR i=1 TO n

FOR j=1 TO n

a(i,j)=a2(i,j)

ENDFOR

ENDFOR

* массив для хранения номеров элементов вектора решений X

FOR i=1 TO n

ix(i)=i

x(i)=0

x1(i)=0

ENDFOR

FOR k=1 TO n-1

* ищем индексы максимального элемента в матрице k x k

im=k

jm=k

max_a=ABS(a(im,jm))

FOR i1 = k TO n

FOR j1 = k TO n

IF ABS(a(i1,j1))>max_a

max_a=ABS(a(i1,j1))

im=i1

jm=j1

ENDIF

ENDFOR

ENDFOR

* переставляем строки k и im

FOR l=k TO n

aa=a(k,l)

a(k,l)=a(im,l)

a(im,l)=aa

ENDFOR

aa=b(k)

b(k)=b(im)

b(im)=aa

* переставляем столбцы k и jm

FOR l=1 TO n

aa=a(l,k)

a(l,k)=a(l,jm)

a(l,jm)=aa

ENDFOR

* переставляем номера k и jm компонент вектора решений X

aa=ix(k)

ix(k)=ix(jm)

ix(jm)=aa

* приводим к треугольному виду

FOR l=k+1 TO n

p=a(l,k)/a(k,k)

FOR m=k TO n

a(l,m)=a(l,m)-a(k,m)*p

ENDFOR

b(l)=b(l)-b(k)*p

ENDFOR

ENDFOR

* вычисляем x

FOR k=n TO 1 STEP -1

s=0

FOR l=k+1 TO n

s=s+a(k,l)*x1(l)

ENDFOR

x1(k)= (b(k)-s)/a(k,k)

ENDFOR

FOR i=1 TO n

x(ix(i))=x1(i)

ENDFOR

ENDPROC

Контрольные вопросы

1. Дать определение системы линейных уравнений.

2. Дать определение вырожденной матрицы.

3. Привести алгоритм метода Гаусса.

4. Привести алгоритм метода Гаусса с выбором максимального элемента.

5. Привести алгоритм приведения матрицы к треугольному виду.

6. Привести алгоритм определения вектора решения системы линейных уравнений, приведенной к треугольному виду (обратный ход метода Гаусса).

7. Дать определение совместности системы линейных уравнений методом Гаусса.

8. Привести алгоритм табуляции характеристической функции.

Задания

Используя метод Гаусса, решить систему линейных уравнений с точностью до 0,0001.

1.

3,21x₁ – 4,25x₂ + 2,13x₃ = 5,06;

7,09x₁ + 1,17x₂ – 2,23x₃ = 4,75;

0,43x₁ – 1,4x₂ – 0,62x₃ = – 1,05.

2.

0,42x₁ – 1,13x₂ + 7,05x₃ = 6,15;

1,14x₁ – 2,15x₂ + 5,11x₃ = – 4,16;

– 0,71x₁ + 0,81x₂ – 0,02x₃ = – 0,17.

3.

2,5x₁ – 3,12x₂ – 4,03x₃ = – 7,5;

0,61x₁ + 0,71x₂ – 0,05x₃ = 0,44;

– 1,03x₁ – 2,05x₂ + 0,877x₃ = – 1,16.

4.

7,09x₁ + 1,17x₂ – 2,23x₃ = – 4,75;

0,43x₁ – 1,4x₂ – 0,62x₃ = –1,05;

3,21x₁ – 4,25x₂ + 2,13x₃ = 5,06.

5.

1,14x₁ – 2,15x₂ – 5,11x₃= – 4,16;

– 0,71x₁ + 0,81x₂ – 0,02x₃ = – 0,17;

0,42x₁ – 1,13x₂ + 7,05x₃ = 6,15.

6.

0,61x₁ + 0,71x₂ – 0,05x₃ = 0,44;

– 1,03x₁ – 2,05x₂ + 0,87x₃ = – 1,16;

2,5x₁ – 3,12x₂ – 5,03x₃ = – 7,5.

7.

3,11x₁ – 1,66x₂ – 0,60x₃ = – 0.92;

– 1,65x₁ + 3,51x₂ – 0,78x₃ = 2,57;

0,60x₁ + 0,78x₂ – 1,87x₃ = 1,65.

8.

0,10x₁ + 12x₂ – 0,13x₃ = 0,10;

0,12x₁ + 0,71x₂ + 0,15x₃ = 0,26;

– 0,13x₁ + 0,15x₂ + 0,63x₃ = 0,38.

9.

0,71x₁ + 0,10x₂ + 0,12x₃ = 0,29;

0,10x₁ + 0,34x₂ – 0,04x₃ = 0,32;

0,12x₁ – 0,04x₂ + 0,10x₃ = – 0,10.

10.

0,34x₁ – 0,04x₂ + 0,10x₃ = 0,33;

– 0,04x₁ + 0,10x₂ + 0,12x₃ = – 0,05;

0,10x₁ + 0,12x₂ + 0,71x₃ = 0,28.

11.

0,12x₁ – 0,43x₂ + 0,14x₃ = –0,17;

–0,07x₁ + 0,34x₂ + 0,72x₃ = 0,62;

1,18x₁ – 0,08x₂ – 0,25x₃ = 1,12.

12.

1,17x₁ + 0,53x₂ – 0,84x₃ = 1,15;

0,64x₁ – 0,72x₂ – 0,43x₃ = 0,15;

0,32x₁ + 0,43x₂ – 0,93x₃ = –0,48.

13.

0,66x₁ – 1,44x₂ – 0,18x₃ = 1,83;

0,48x₁ – 0,24x₂ + 0,37x₃ = – 0,84;

0,86x₁ + 0,43x₂ + 0,64x₃ = 0,64.

14.

0,82x₁ + 0,43x₂ – 0,57x₃ = 0,48;

–0,35x₁ + 1,12x₂ – 0,48x₃ = 0,52;

0,48x₁ + 0,23x₂+0,37x₃ = 1,44.

15.

1,6x₁ + 0,12x₂ + 0,57x₃ = 0,18;

0,38x₁ + 0,25x₂ – 54x₃ = 0,63;

0,28x₁ + 0,46x₂ – 1,12x₃ = 0,88.

16.

1,16x₁ + 1,3x₂ – 1,14x₃ = 0,43;

0,83x₁ – 0,48x₂ – 2,44x₃ = –0,15;

2x₁ – 0,16x₂ + 1,3x₃ = 1,5.

17.

0,10x₁ – 0,04x₂ – 0,13x₃ = – 0,15;

– 0,04x₁ + 0,34x₂+0,05x₃ = 0,31;

–0,13x₁ + 0,05x₂ + 0,63x₃ = 0,37.

18.

0,63x₁ + 0,05x₂ + 0,15x₃ = 0,34;

0,05x₁ + 0,34x₂ + 0,10x₃ = 0,32;

0,15x₁ + 0,10x₂ + 0,71x₃ = 0,42.

19.

1,20x₁ – 0,20x₂ + 0,30x₃ = –0,60;

– 0,20x₁ + 1,60x₂ – 0,10x₃ = 0,30;

– 0,30x₁ + 0,10x₂ – 1,5x₃ = 0,40.

20.

0,30x₁ + 1,20x₂ – 0,20x₃ = –0,60;

– 0,10x₁ – 0,20x₂ + 1,60x₃ = 0,30;

–1,50x₁ – 0,30x₂ + 0,10x₃ = 40.

21.

0,20x₁ + 0,44x₂ + 0,81x₃ = 0,74;

0,58x₁ – 0,29x₂ + 0,05x₃ = 0,02;

0,05x₁ + 0,34x₂ + 0,10x₃ = 0,32.

22.

6,36x₁ + 11,75x₂ + 10x₃ = –41,70;

7,42x₁ + 19,03x₂ + 11,75x₃ = –49,49;

5,77x₁ + 7,42x₂ + 6,36x₃ = –27,67.

23.

0,40x₁ + 0,11x₂ + 0,18x₃ = 0,47;

0,28x₁ – 0,59x₂ + 0,03x₃ = 0,01;

0,02x₁ + 0,24x₂ + 0,10x₃ = 0,22.

24.

0,18x₁ + 0,25x₂ – 0,44x₃ = 1,15;

0,42x₁ – 0,35x₂ + 1,12x₃ = 0,86;

1,14x₁ + 0,12x₂ – 0,83x₃ = 0,68.

25.

1,2x₁ + 0,18x₂ – 0,42x₃ = 1,5;

0,44x₁ + 0,36x₂ + 0,12x₃ = 1,16;

0,36x₁ – 0,42x₂ – 0,22x₃ = 0,15.

26.

0,64x₁ – 0,43x₂ + 0,57x₃ = 0,43;

0,56x₁ + 0,12x₂ – 0,27x₃ = 0,88;

0,63x₁ – 0,83x₂ + 0,43x₃ = – 0,12.

27.

1,60x₁ + 2,18x₂ – 0,72x₃ = 1,15;

0,43x₁ – 0,16x₂ + 0,53x₃ = 0,83;

0,34x₁ + 0,57x₂ – 0,83x₃ = – 0,42.

28.

0,8x₁ – 0,13x₂ + 0,63x₃ = 1,15;

0,42x₁ + 0,57x₂ + 0,32x₃ = 0,84;

0,54x₁ + 0,62x₂ – 0,32x₃ =0,25