Основное свойство обыкновенной дроби

Вспомним основное свойство обыкновенной дроби: значение дроби не изменится, если ее числитель и знаменатель одновременно умножить или разделить на одно и то же отличное от нуля число. Напомним, что деление числителя и знаменателя дроби на одно и то же отличное от нуля число называется сокращением.

Например: , при этом значение дробей не изменяется. Однако зачастую при применении данного свойства многие допускают стандартные ошибки:

1. 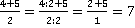– в приведенном примере допущена ошибка деления только одного слагаемого из числителя на 2, а не всего числителя. Правильная последовательность действий выглядит таким образом: или .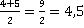

2. – здесь мы видим похожую ошибку, однако, кроме этого еще в результате деления 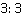получен 0, а не 1, что является еще более частой и грубой ошибкой.

Теперь необходимо перейти к рассмотрению алгебраической дроби. Вспомним это понятие из предыдущего урока.

Определение.Рациональная (алгебраическая) дробь – дробное выражение вида , где 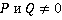– многочлены. – числитель, – знаменатель.

Алгебраические дроби являются, в некотором смысле, обобщением обыкновенных дробей, и над ними можно проводить те же операции, что и над обыкновенными дробями.

Основное свойство алгебраической дроби

Основное свойство алгебраической дроби – и числитель, и знаменатель дроби можно умножать и делить на один и тот же многочлен (одночлен) или число, отличное от нуля. Это будет тождественное преобразование алгебраической дроби. Вспомним, что, как и ранее, деление числителя и знаменателя дроби на одно и то же отличное от нуля выражение называется сокращением.

Основное свойство алгебраической дроби позволяет сокращать дроби и приводить их к наименьшему общему знаменателю.

Примеры сокращения обыкновенных дробей

Для сокращения обыкновенных дробей мы прибегали к основной теореме арифметики, разлагали и числитель, и знаменатель на простые множители.

Определение. Простое число – натуральное число, которое делится только на единицу и само себя. Все остальные натуральные числа называются составными. 1 не является ни простым, ни составным числом.

Пример 1.а) 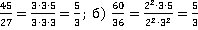, где множители, на которые разложены числители и знаменатели указанных дробей, являются простыми числами.

Ответ: ; .

Примеры сокращения алгебраических дробей

Следовательно, для сокращения дробей необходимо предварительно разложить на множители числитель и знаменатель дроби, а затем разделить их на общие множители. Т. е. следует владеть методами разложения многочленов на множители.

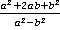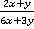Пример 2. Сократить дробь а) ,б) , в) .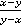

Решение. а) 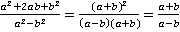. Необходимо заметить, что в числителе находится полный квадрат, а в знаменателе – разность квадратов. После сокращения необходимо указать, что 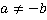, во избежание деления на ноль.

б) 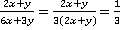. В знаменателе выносится общий числовой множитель, что полезно делать практически в любом случае, когда это возможно. Аналогично с предыдущим примером указываем, что .

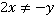в) 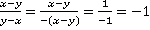. В знаменателе выносим за скобки минус (или, формально, 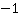). Не забываем, что при сокращении .

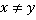Ответ. ; ; .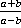

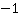Теперь приведём пример на приведение к общему знаменателю, делается это аналогично с обыкновенными дробями.