Фундаментальная система решений

Система линейных уравнений называется однородной, если все ее свободные члены равны нулю.

Фундаментальной системой решений однородной системы линейных уравнений называется базис множества ее решений.

Пусть дана неоднородная система линейных уравнений. Однородной системой, ассоциированной с данной, называется система, полученная из данной заменой всех свободных членов на нули.

Если неоднородная система совместна и неопределенна, то ее произвольное решение имеет вид f_н + l₁f_о1+ ... + l_kf_оk , где f_н – частное решение неоднородной системы и f_о1, ... , f_оk – фундаментальная система решений ассоциированной однородной системы.

П р и м е р 3. Найти частное решение неоднородной системы из примера 1 и фундаментальную систему решений ассоциированной однородной системы.

Р е ш е н и е. Запишем решение, полученное в примере 1, в векторном виде и разложим получившийся вектор в сумму по свободным параметрам, имеющимся в нем, и фиксированным числовым значениям:

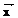= (x₁, x₂, x₃, x₄) = (–2a + 7b – 2, a, – 2b + 1, b) = (–2a, a, 0, 0) + (7b, 0, –2b, b) + +(– 2, 0, 1, 0) = a(-2, 1, 0, 0) + b(7, 0, -2, 1) + (– 2, 0, 1, 0).

_­­Получаем f_н = (– 2, 0, 1, 0), f_о1= (-2, 1, 0, 0), f_о2= (7, 0, -2, 1).

Замечание. Аналогично решается задача нахождения фундаментальной системы решений однородной системы.

У п р а ж н е н и е 3.1 Найти фундаментальную систему решений однородной системы:

а)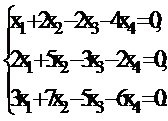

б)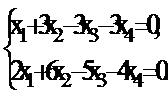

в) 2x₁ – x₂ +3x₃ = 0.

У п р а ж н е н и е 3.2. Найти частное решение неоднородной системы и фундаментальную систему решений ассоциированной однородной системы:

а)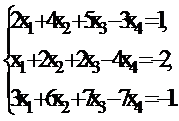

б)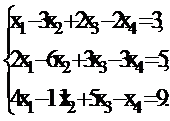

Алгебра матриц

На множестве матриц определены операции сложения, умножения на скаляры, умножения матриц.

Складывать можно прямоугольные матрицы одного и того же порядка. Сложение выполняется покомпонентно.

Умножать на скаляр можно любую матрицу. Умножение выполняется покомпонентно (то есть каждый элемент матрицы умножается на скаляр).

Умножать можно матрицу порядка m´k на матрицу порядка k´n, то есть длина строки первой матрицы должна быть равна длине столбца второй матрицы В произведении получится матрица порядка m´n. Ее элемент, находящийся в i-ой строке и j-ом столбце, получается умножением элементов i-ой строки первой матрицы на соответствующие элементы j-ого столбца второй матрицы и сложением получившихся произведений.

П р и м е р 4.1.

= = .

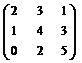
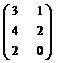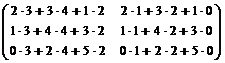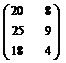Матрицей, транспонированной к матрице А, называется матрица А^Т, строки которой совпадают с соответствующими столбцами матрицы А.

Обратной к квадратной матрице А называется матрица А^-1_­ такая, что

А×А^-1 = А^-1×А = Е, где Е – единичная матрица,

Е = .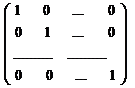

Для нахождения обратной матрицы к матрице А строим новую матрицу, расположив рядом матрицы А и Е и отделив их друг от друга вертикальной чертой. Соответствующие строки матриц А и Е образуют единую строку новой матрицы. Элементарными преобразованиями строк приводим матрицу А к единичному виду. Тогда матрица Е преобразуется к А^-1.

П р и м е р 4.2. Найти матрицу, обратную к матрице

А = .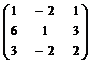

Р е ш е н и е. Объединяем матрицы А и Е и приводим матрицу А к единичной:

~ ~

~ ~ ~

~ ~ .

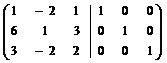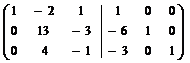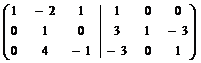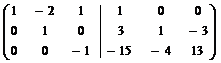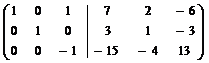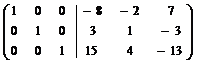Следовательно,

А^-1 = .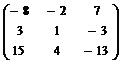

У п р а ж н е н и е 4.1 Найти обратную матрицу:

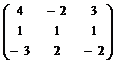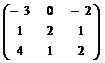а) ; б) ; в) .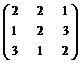

У п р а ж н е н и е 4.2. Решить матричное уравнение:

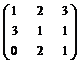X = .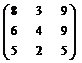

Определители

Определители второго и третьего порядка вычисляются по формулам

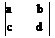= ad – bc;

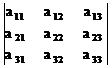= a₁₁a₂₂a₃₃ + a₁₂a₂₃a₃₁ + a₁₃a₂₁a₃₂ - a₁₃a₂₂a₃₁ - a₁₂a₂₁a₃₃ - a₁₁a₂₃a₃₂.

Для вычисления определителей более высокого порядка их порядок следует понизить. Для этого пользуются правилами:

1) если к строке (столбцу) матрицы прибавить другую строку (столбец), умноженную на произвольный скаляр, то ее определитель не изменится;

2) если строку (столбец) матрицы умножить на скаляр l, то на l умножится ее определитель;

3) если поменять местами две строки (столбца) матрицы, то ее определитель поменяет знак;

4) определитель матрицы с нулевой строкой (столбцом) равен 0;

5) определитель матрицы А, у которой все элементы какой-либо строки (столбца), кроме, может быть, a_ij, равны 0, равен (-1)^i+ja_ijM_ij, где M_ij – определитель матрицы, полученной из А вычеркиванием i-ой строки и j-го столбца.

Для понижения порядка определителя выбираем в нем какой-нибудь элемент, обычно равный 1. Используя строку, в которой он стоит, как опорную, с помощью правила 1) как в методе Гаусса заменяем остальные элементы столбца, в котором стоит выбранный элемент, на нули. После этого понижаем порядок определителя по правилу 5). Можно и поменять строки и столбцы ролями, делая нули не в столбце, а в строке.

П р и м е р 5.1. Вычислить определитель

.

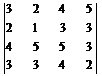Р е ш е н и е. Мы имеем элемент 1 на пересечении второй строки и второго столбца. Используя вторую строку, сделаем остальные элементы во втором столбце равными 0. Для этого к первой, третьей и четвертой строкам прибавляем вторую, умноженную на –2, -5, -3 соответственно. Получаем:

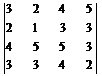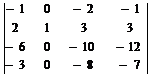= =(-1)²⁺² = =

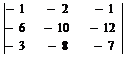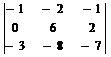= 42 + 12 + 0 – 18 – 16 – 0 = 20.

Перед вычислением определителя третьего порядка его упростили, прибавив ко второй строке третью, умноженную на –2.

У п р а ж н е н и е 5.1. Вычислить определители:

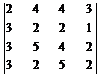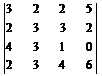а) ; б) ; в) .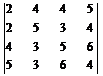

Минором элемента a_ij квадратной матрицы А называется определитель матрицы, полученной из А вычеркиванием i-ой строки и j-ого столбца (в которых стоит элемент a_ij).

Алгебраическим дополнением элемента a_ij квадратной матрицы А называется скаляр A_ij = (-1)^i+j M_ij, где M_ij – минор элемента a_ij.

Матрицу, обратную к матрице А, можно вычислить по формуле

A^-1 = ïAï^-1 A^*,

где A^* – матрица, полученная из А заменой каждого элемента его алгебраическим дополнением и последующим транспонированием.

П р и м е р 5.2. Найти матрицу, обратную к

А = .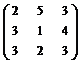

Р е ш е н и е. Имеем

ïAï = 6 + 18 + 60 – 9 – 16 – 45 = 14;

A^* = ;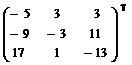

A^-1 = .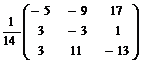

У п р а ж н е н и е 5.2. Найти обратную матрицу методом алгебраических дополнений:

а) 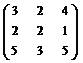; б) 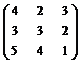.