Системы линейных однородных уравнений.

ФУНДАМЕНТАЛЬНАЯ СИСТЕМА РЕШЕНИЙ

Система линейных уравнений называется однородной, если все свободные члены уравнений равны нулю:

Однородная система всегда совместна, поскольку она всегда имеет тривиальное (нулевое) решение. Однако наибольший интерес представляют нетривиальные решения.

Теорема 1. Однородная система линейных уравнений имеет нетривиальное решение тогда и только тогда, когда ранг матрицы системы меньше числа неизвестных: r(A)=r<n.

Справедливо следующее утверждение: линейная комбинация решений однородной системы линейных уравнений также является ее решением.

Максимальная линейно независимая система решений называется фундаментальной системой решений однородной системы уравнений. Фундаментальная система решений содержит (n-r) векторов. Любое решение системы может быть представлено в виде линейной комбинации векторов фундаментальной системы решений.

Для нахождения фундаментальной системы решений нужно:

1) r базисных переменных выразить через свободные переменные;

2) выбрать линейно независимую систему (n-r) векторов (n-r)-мерного пространства (например, это могут быть единичные векторы);

3) поочередно заменить свободные переменные координатами векторов выбранной системы и вычислить значения базисных переменных.

Полученные решения 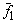, , 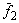…, 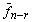образуют фундаментальную систему решений. Тогда общее решение однородной системы уравнений имеет вид

,

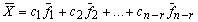где 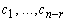- произвольные числа.

Билет 13

МНОГОЧЛЕН

МНОГОЧЛЕН (полином), сумма одночленов, которые являются произведениями, состоящими из числового множителя (коэффициента) и одной или нескольких букв, каждая из которых взята с тем или иным показателем степени. В общем виде, многочлен имеет форму P_n(x)=а_nхⁿ+a_n-1x^n-1+а_n-2х^n-2+....+а₂х²+a₁х+а₀, где а₀....а_n-1, а_n - КОЭФФИЦИЕНТЫ многочлена. Степенью многочлена является самый высокий показатель степени в этой сумме с ненулевым коэффициентом. Например, Р₄(х)=2x⁴-3x³+x²+х+5 является многочленом со степенью четыре. В этом примере значения многочлена при х=0; 1 и 2 равны Р₄(0)=5, Р₄(1)=6, Р₄(2)=19 соответственно. Многочлен может быть представлен графически, путем отметки значения у=Р_n(х) на графике в соответствии со значениями х.

Арифметические операции над многочленами

Суммой многочленов

P(x)=a0xn+a1xn−1+...+an−1x+an,

Q(x)=b0xm+b1xm−1+...+bm−1x+bm

называется многочлен S(x), коэффициенты которого при каждой степени x равны сумме коэффициентов при этой степени x многочленов P(x) и Q(x). О многочлене S(x) говорят, что он получен в результате сложения многочленов P(x) и Q(x), и пишут S(x)=P(x)+Q(x).

Произведением многочленов

P(x)=a0xn+a1xn−1+...+an−1x+an,

Q(x)=b0xm+b1xm−1+...+bm−1x+bm

называется многочлен M(x) степени n+m, коэффициенты которого c0,c1,...,cn+m вычисляются по формулам

c0=a0b0, c1=a1b0+a0b1, ... ck=akb0+ak−1b1+...+a1bk−1+a0bk, cn+m=anbm,

т.е. коэффициент ci есть сумма произведений коэффициентов al и bk многочленов P(x) и Q(x) таких, что сумма их индексов равна i=l+k. О многочлене M(x) говорят, что он получен в результате умножения многочлена P(x) на многочлен Q(x), и пишут M(x)=P(x)Q(x).

Операции сложения и умножения многочленов ассоциативны, коммутативны и связаны между собой законом дистрибутивности.

Противоположным для многочлена

P(x)=a0xn+a1xn−1+...+an−1x+an

называется многочлен

−a0xn−a1xn−1−...−an−1x−an

Многочлен, противоположный многочлену P(x), обозначают −P(x) . Сумма многочлена P(x) и противоположного ему многочлена −P(x) равна нулю: P(x)+(−P(x))=0

Разностью многочленов P(x) и Q(x) называется многочлен L(x), являющийся суммой многочлена P(x)и многочлена, противоположного многочлену Q(x):

L(x)=P(x)+(−Q(x))

О многочлене L(x) говорят, что он получен в результате вычитания многочлена Q(x) из многочлена P(x), и пишут L(x)=P(x)−Q(x) .

Сумма, произведение и разность любых двух многочленов - тоже многочлены.

Деление с остатком

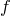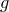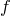Определение. Пусть и — многочлены, . Будем говорить, что поделен на 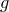с остатком, если 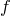представлен в виде 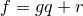, где и — многочлены, причем .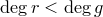

Полином называется остатком от деления 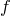на 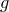, — неполным частным.

Пример. .

.

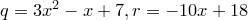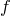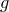Теорема. (о делении с остатком). Пусть и — полиномы над полем , . Тогда существуют единственные многочлены и над полем такие, что 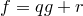и .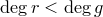

Доказательство. Существование.

Пусть . Положим .

.

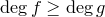Предположим, что теорема верна не для любого полинома 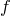( 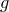фиксируем). Среди всех многочленов 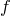, для которых теорема неверна, выберем многочлен наименьшей степени и обозначим его :

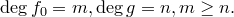
Пусть 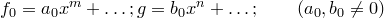. Положим

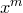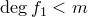Коэффициент при в многочлене равен . Следовательно, . Значит, для многочлена теорема верна. Существуют такие и , что 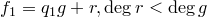. Тогда

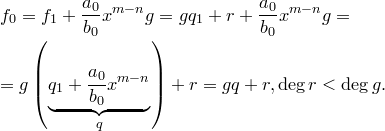
Получили противоречие с тем предположением, что есть многочлены, для которых теорема неверна.

Единственность. Предположим, что

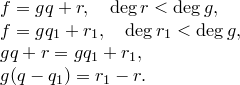
1) 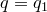. Значит, ,

2) .

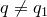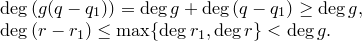
Получили противоречие. Этот случай невозможен.

Схе́ма Го́рнера (или правило Горнера, метод Горнера) — алгоритм вычисления значения многочлена, записанного в виде суммы мономов (одночленов), при заданном значении переменной. Метод Горнера позволяет найти корни многочлена^[1], а также вычислить производные полинома в заданной точке. Схема Горнера также является простым алгоритмом для деления многочлена на бином вида 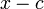. Метод назван в честь Уильяма Джорджа Горнера (англ.).

Описание алгоритма

Задан многочлен :

.

Пусть требуется вычислить значение данного многочлена при фиксированном значении 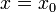. Представим многочлен в следующем виде:

.

Определим следующую последовательность:

…

…

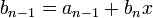
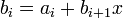
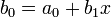
Искомое значение 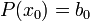. Покажем, что это так.

В полученную форму записи подставим 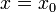и будем вычислять значение выражения, начиная со внутренних скобок. Для этого будем заменять подвыражения через :

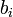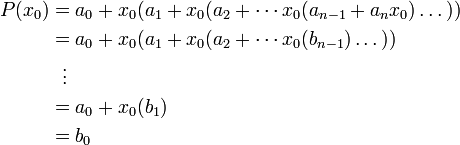
Использование схемы Горнера для деления многочлена на бином

При делении многочле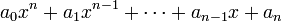на на 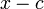получается многочлен 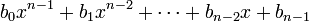с остатком .

При этом коэффициенты результирующего многочлена удовлетворяют рекуррентным соотношениям:

, .

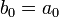Таким же образом можно определить кратность корней (использовать схему Горнера для нового полинома). Так же схему можно использовать для нахождения коэффициентов при разложении полинома по степеням :

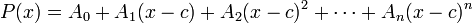
Билет 14

Корень многочлена (не равного тождественно нулю)

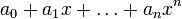
над полем k — элемент , такой что выполняются два следующих равносильных условия:

§ данный многочлен делится на многочлен ;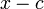

§ подстановка элемента c вместо x обращает уравнение

в тождество.

Равносильность двух формулировок следует из теоремы Безу. В различных источниках любая одна из двух формулировок выбирается в качестве определения, а другая выводится в качестве теоремы.

Свойства

§ Число корней многочлена степени не превышает даже в том случае, если кратные корни учитывать кратное количество раз.

§ Всякий многочлен с комплексными коэффициентами имеет по крайней мере один, вообще говоря, комплексный, корень (основная теорема алгебры) .

§ Аналогичное утверждение верно для любого алгебраически замкнутого поля (по определению).

§ Более того, многочлен с вещественными коэффициентами можно записать в виде

где 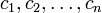— (в общем случае комплексные) корни многочлена , возможно с повторениями, при этом если среди корней 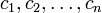многочлена встречаются равные, то общее их значение называется кратным корнем.

§ Число комплексных корней многочлена с комплексными коэффициентами степени , учитывая кратные корни кратное количество раз, равно . При этом все чисто комплексные корни (если они есть) многочлена с вещественными коэффициентами можно разбить на пары сопряжённых одинаковой кратности, таким образом, многочлен четной степени с вещественными коэффициентами может иметь только чётное число вещественных корней, а нечётной — только нечётное.

§ Корни многочлена связаны с его коэффициентами формулами Виета.

Теорема Безу

Теорема Безу утверждает, что остаток от деления многочлена на двучле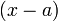н равен .

Предполагается, что коэффициенты многочлена содержатся в некотором коммутативном кольце с единицей (например, в поле вещественных или комплексных чисел).

Доказательство

Поделим с остатком многочлен на многочлен :

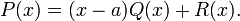
Так как 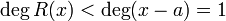, то 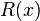— многочлен степени не выше 0. Подставляя , поскольку , имеем .

Следствия

· Число a является корнем многочлена тогда и только тогда, когда делится без остатка на двучлен (отсюда, в частности, следует, что множество корней многочлена тождественно множеству корней соответствующего уравнения ).

· Свободный член многочлена делится на любой целый корень многочлена с целыми коэффициентами (если старший коэффициент равен 1, то все рациональные корни являются и целыми).

· Пусть α — целый корень приведённого многочлена A(x) с целыми коэффициентами. Тогда для любого целого k число A(k) делится на α-k.

Кратные корни

· Определение. Число 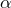называется корнем полинома 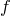, если .

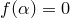· В силу теоремы Безу это равносильно тому, что .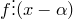

· Определение. Число 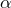называется корнем кратности полинома 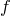, есл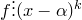и и 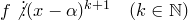. Корни кратности 1 называются простыми корнями, корни кратности больше 1 называются кратными корнями.

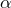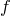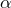· Теорема. Если — корень кратности полинома , то — корень кратности 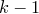полинома . Если 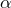— общий корень 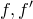, то 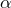— кратный корень .

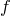· Доказательство. Пусть 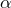— корень кратности полинома .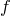

·

·

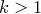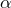· 1. Если , то — корень кратности 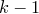многочлена .

· 2. Если 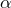корень , то 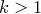и, значит, 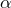— кратный корень многочлена .

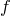Теорема Виета

·

· Как связаны между собой корни квадратного трехчлена x² + px + q и его коэффициенты p и q? Ответ на этот вопрос дает теорема, которая носит имя “отца алгебры”, французского математика Ф. Виета, жившего в конце XVI века.

Теорема.

Сумма корней квадратного трехчлена x² + px + q равна его второму коэффициенту p с противоположным знаком, а произведение – свободному члену q.

Доказательство. Пусть x₁ и x₂ – различные корни квадратного трехчлена x² + px + q. Теорема Виета утверждает, что имеют место следующие соотношения:

x₁ + x₂ = –p

x₁ x₂ = q

Для доказательства подставим каждый из корней в выражение для квадратного трехчлена. Получим два верных числовых равенства:

x₁² + px₁ + q = 0

x₂² + px₂ + q = 0

Вычтем эти равенства друг из друга. Получим

x₁² – x₂² + p (x₁ – x₂) = 0

Разложим разность квадратов и одновременно перенесем второе слагаемое в правую часть:

(x₁ – x₂) (x₁ + x₂) = –p (x₁ – x₂)

Так как по условию корни x₁ и x₂ различны, то x₁ – x₂ ¹ 0 и мы можем сократить равенство на x₁ – x₂. Получим первое равенство теоремы:

x₁ + x₂ = –p

Для доказательства второго подставим в одно из написанных выше равенств (например, в первое) вместо коэффициента p,равное ему число – (x₁ + x₂):

x₁² – (x₁ + x₂) x₁ + q = 0

Преобразуя левую часть, получаем:

x₁² – x₁² – x₂ x₁ + q = 0

x₁ x₂ = q, что и требовалось доказать.

Комментарий. Теорема Виета замечательна тем, что, не зная корней квадратного трехчлена, мы легко можем вычислить их сумму и произведение, то есть простейшие симметричные выражения x₁ + x₂ и x₁ x₂. Так, еще не зная, как вычислить корни уравнения x² – x – 1 = 0, мы, тем не менее, можем сказать, что их сумма должна быть равна 1, а произведение должно равняться –1.

Теорема Виета позволяет угадывать целые корни квадратного трехчлена. Так, находя корни квадратного уравнения x² – 5x + 6 = 0, можно начать с того, чтобы попытаться разложить свободный член (число 6) на два множителя так, чтобы их сумма равнялась бы числу 5. Это разложение очевидно: 6 = 2 × 3, 2 + 3 = 5. Отсюда должно следовать, что числа 2 и 3 являются искомыми корнями. Эту догадку можно аккуратно доказать.

Теорема. Если числа x₁ и x₂ удовлетворяют соотношениям x₁ + x₂ = –p и x₁ x₂ = q, то они удовлетворяют квадратному уравнению x² + px + q = 0.

Доказательство. Из первого из данных равенств выразим x₂ и подставим во второе: x₂ = –p – x₁, x₁ × x₂ = x₁ × (–p – x₁) = q. Получаем –x₁² – px₁ = q или x₁² + px₁ + q = 0. Это означает, что число x₁ является корнем квадратного уравнения x² + px + q = 0. Если бы наоборот мы выразили x₁ через x₂, то получили бы и для x₂ аналогичное соотношение:x₂² + px₂ + q = 0. Теорема доказана.

Формулы Виета — формулы, выражающие коэффициенты многочлена через его корни.

Этими формулами удобно пользоваться для проверки правильности нахождения корней многочлена, а также для составления многочлена по заданным корням.

Формулировка

Если — корни многочлена

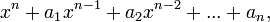
(каждый корень взят соответствующее его кратности число раз), то коэффициенты выражаются в виде симметрических многочленов от корней, а именно:

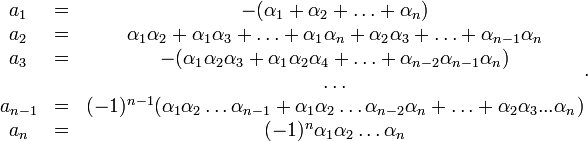
Иначе говоря 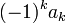равно сумме всех возможных произведений из 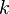корней.

Если старший коэффициент многочлена 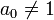, то для применения формулы Виета необходимо предварительно разделить все коэффициенты на 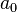(это не влияет на значение корней многочлена). В этом случае формулы Виета дают выражение для отношений всех коэффициентов к старшему. Из последней формулы Виета следует, что если корни многочлена целочисленные, то они являются делителями его свободного члена, который также целочисленен.

[править]Доказательство

Доказательство осуществляется рассмотрением равенства, полученного разложением многочлена по корням, учитывая, что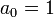

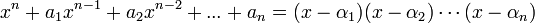
Приравнивая коэффициенты при одинаковых степенях (теорема единственности), получаем формулы Виета.

Билет 16

Алгоритм Евклида для целых чисел

Пусть 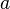и — целые числа, не равные одновременно нулю, и последовательность чисел

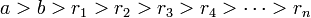
определена тем, что каждое — это остаток от деления предпредыдущего числа на предыдущее, а предпоследнее делится на последнее нацело, то есть

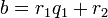
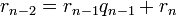
Тогда НОД(a,b), наибольший общий делитель 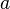и , равен 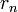, последнему ненулевому члену этой последовательности.

Существование таких , то есть возможность деления с остатком на для любого целого и целого 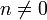, доказывается индукцией по m.

Корректность этого алгоритма вытекает из следующих двух утверждений:

Пусть 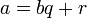, тогда НОД (a, b) = НОД (b, r).

Доказательство[показать]

НОД(0, ) = для любого ненулевого (т.к. 0 делится на любое целое число, кроме нуля).

Проще сформулировать алгоритм Евклида так: если даны натуральные числа 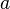и и, пока получается положительное число, по очереди вычитать из большего меньшее, то в результате получится НОД.