Вычисление ранга матрицы с помощью миноров

Ранг матрицы находится либо методом окаймления миноров, либо методом элементарных преобразований. При вычислении ранга матрицы первым способом следует переходить от миноров низших порядков к минорам более высокого порядка. Если уже найден минор D k-го порядка матрицы А, отличный от нуля, то требуют вычисления лишь миноры (k+1)-го порядка, окаймляющие минор D, т.е. содержащие его в качестве минора. Если все они равны нулю, то ранг матрицы равен k.

Пример 1. Найти методом окаймления миноров ранг матрицы

.

Решение. Начинаем с миноров 1-го порядка, т.е. с элементов матрицы А. Выберем, например, минор (элемент) М₁ = 1, расположенный в первой строке и первом столбце. Окаймляя при помощи второй строки и третьего столбца, получаем минор M₂ = , отличный от нуля. Переходим теперь к минорам 3-го порядка, окаймляющим М₂. Их всего два (можно добавить второй столбец или четвертый). Вычисляем их: = 0. Таким образом, все окаймляющие миноры третьего порядка оказались равными нулю. Ранг матрицы А равен двум.

Вычисление ранга матрицы с помощью элементарных преобразований

Элементарными называются следующие преобразования матрицы:

1) перестановка двух любых строк (или столбцов),

2) умножение строки (или столбца) на отличное от нуля число,

3) прибавление к одной строке (или столбцу) другой строки (или столбца), умноженной на некоторое число.

Две матрицы называются эквивалентными, если одна из них получается из другой с помощью конечного множества элементарных преобразований.

Эквивалентные матрицы не являются, вообще говоря, равными, но их ранги равны. Если матрицы А и В эквивалентны, то это записывается так: A ~ B.

Канонической матрицей называется матрица, у которой в начале главной диагонали стоят подряд несколько единиц (число которых может равняться нулю), а все остальные элементы равны нулю, например,

.

При помощи элементарных преобразований строк и столбцов любую матрицу можно привести к канонической. Ранг канонической матрицы равен числу единиц на ее главной диагонали.

Пример 2 Найти ранг матрицы

А=

и привести ее к каноническому виду.

Решение. Из второй строки вычтем первую и переставим эти строки:

.

Теперь из второй и третьей строк вычтем первую, умноженную соответственно на 2 и 5:

;

из третьей строки вычтем первую; получим матрицу

В = ,

которая эквивалентна матрице А, так как получена из нее с помощью конечного множества элементарных преобразований. Очевидно, что ранг матрицы В равен 2, а следовательно, и r(A)=2. Матрицу В легко привести к канонической. Вычитая первый столбец, умноженный на подходящие числа, из всех последующих, обратим в нуль все элементы первой строки, кроме первого, причем элементы остальных строк не изменяются. Затем, вычитая второй столбец, умноженный на подходящие числа, из всех последующих, обратим в нуль все элементы второй строки, кроме второго, и получим каноническую матрицу:

.

Билет 11

Система m линейных алгебраических уравнений с n неизвестными (или, линейная система, также употребляется аббревиатура СЛА́У) в линейной алгебре — это система уравнений вида

(1)

Система линейных уравнений от трёх переменных определяет набор плоскостей. Точка пересечения является решением.

Здесь 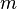— количество уравнений, а 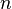— количество неизвестных. x₁, x₂, …, x_n — неизвестные, которые надо определить. a₁₁,a₁₂, …, a_mn — коэффициенты системы — и b₁, b₂, … b_m — свободные члены — предполагаются известными^[1]. Индексы коэффициентов (a_ij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно^[2].

Система (1) называется однородной, если все её свободные члены равны нулю (b₁ = b₂ = … = b_m = 0), иначе — неоднородной.

Система (1) называется квадратной, если число m уравнений равно числу n неизвестных.

Решение системы (1) — совокупность n чисел c₁, c₂, …, c_n, таких что подстановка каждого c_i вместо x_i в систему (1) обращает все её уравнения в тождества.

Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения.

Совместная система вида (1) может иметь одно или более решений.

Решения c₁⁽¹⁾, c₂⁽¹⁾, …, c_n⁽¹⁾ и c₁⁽²⁾, c₂⁽²⁾, …, c_n⁽²⁾ совместной системы вида (1) называются различными, если нарушается хотя бы одно из равенств:

c1(1) = c1(2), c2(1) = c2(2), …, cn(1) = cn(2).

Совместная система вида (1) называется определённой, если она имеет единственное решение; если же у неё есть хотя бы два различных решения, то она называетсянеопределённой. Если уравнений больше, чем неизвестных, она называется переопределённой.

Матричная форма

Система линейных уравнений может быть представлена в матричной форме как:

или:

.

Здесь 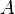— это матрица системы, 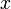— столбец неизвестных, а 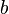— столбец свободных членов. Если к матрице 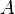приписать справа столбец свободных членов, то получившаяся матрица называется расширенной.

[править]Эквивалентные системы линейных уравнений

Системы линейных уравнений называются эквивалентными, если множество их решений совпадает, то есть любое решение одной системы одновременно является решением другой, и наоборот.

Систему, эквивалентную данной, можно получить, в частности, заменив одно из уравнений на это уравнение, умноженное на любое отличное от нуля число. Эквивалентную систему можно получить также, заменив одно из уравнений суммой этого уравнения с другим уравнением системы. В общем, замена уравнения системы на линейную комбинацию уравнений даёт систему, эквивалентную исходной.

Система линейных алгебраических уравнений

эквивалентна системе

,

где — невырожденная матрица.

В частности, если сама матрица 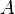— невырожденная, и для неё существует обратная матрица , то решение системы уравнений можно формально записать в виде

.

Теорема Кронекера-Капелли

Для того чтобы система m неоднородных линейных уравнений с n неизвестными была совместной, необходимо и достаточно, чтобы Доказательство необходимости. Пусть система (1.13) совместна, то есть существуют такие числа х1=α1, х2=α2, …, хn=αn, что (1.15) Вычтем из последнего столбца расширенной матрицы ее первый столбец, умноженный на α1, второй – на α2, …, n-ый – умноженный на αn, то есть из последнего столбца матрицы (1.14) следует вычесть левые части равенств (1.15). Тогда получим матрицу ранг которой в результате элементарных преобразований не изменится и . Но очевидно, и, значит, Доказательство достаточности. Пусть и пусть для определенности не равный нулю минор порядка r расположен в левом верхнем углу матрицы: Это означает, что остальные строки матрицы могут быть получены как линейные комбинации первых r строк, то есть m-r строк матрицы можно представить в виде сумм первых r строк, умноженных на некоторые числа. Но тогда первые r уравнений системы (1.13) самостоятельны, а остальные являются их следствиями, то есть решение системы первых r уравнений автоматически является решением остальных уравнений. Возможны два случая. 1. r=n. Тогда система, состоящая из первых r уравнений, имеет одинаковое число уравнений и неизвестных и совместна, причем решение ее единственно. 2. r<n. Возьмем первые r уравнений системы и оставим в левых частях этих уравнений первые r неизвестных, а остальные – перенесем вправо: (1.16) «Свободным» неизвестным xr+1, xr+2, …, xn можно придать какие угодно значения. Тогда соответствующие значения получают неизвестные x1, x2, …, xr. Система (1.13) и в этом случае совместная, но неопределенная. Замечание. Отличный от нуля минор порядка r, где r<n, будем называть базисным минором. Неизвестные х1, х2, …, хr так же называют базисными, остальные – свободными. Систему (1.16) называют укороченной. Если свободные неизвестные обозначить хr+1=c1, хr+2=c2, …, хn=cn-r, то базисные неизвестные будут от них зависеть, то есть решение системы m уравнений с n неизвестными будет иметь вид X = (x1(c1, …, cn-r), x2(c1, …, cn-r), …, xr(c1, …, cn-r), c1, c2, …, cn-r)T, где значок Т означает транспонирование. Такое решение системы называется общим.

Билет 12