Алгебра и аналитическая геометрия
АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Учебное пособие
(часть I)
Ростов-на-Дону
УДК 517
Ш31
Ш31 Шевченко Н.П., Смирнова И.Ю. Алгебра и аналитическая геометрия. Учеб. пособие (часть I). Ростов-на-Дону: Издательский центр ДГТУ. 2004. 30с.
Учебное пособие (часть I) представляет собой опорный конспект лекций и упражнений по теме: «Множества, элементы математической логики, векторная алгебра». Рассмотрены основные понятия, свойства, приведены примеры с решениями. Пособие рассчитано на студентов первого курса всех специальностей, изучающих указанные разделы курса Высшая математика.
Печатается по решению редакционно-издательского совета
Донского государственного технического университета.
Научный редактор д.ф.-м. н., проф. А.В. Братищев.
Рецензенты: к. ф.-м. н. Т.Н. Радченко (РГУ, г. Ростов-на-Дону)
©Издательский центр ДГТУ, 2004
Лекция 1. Множества.
Множество-это неопределяемое понятие, смысл которого ясен на основании практической деятельности человека. “Объекты”, входящие в состав множества, называются элементами заданного множества. Множества, элементами которых являются числа, называются числовыми множествами. Стандартные числовые множества:
N-множество натуральных чисел: {1, 2, 3,…},
Z-множество всех целых чисел: {0,  1,
1,  2,…},
2,…},
Z0-множество всех неотрицательных целых чисел: {0, 1, 2, …},
Q-множество рациональных чисел: {  }, m, n
}, m, n 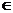 N,
N,
R-множество действительных чисел, I-множество иррациональных чисел
Множества обозначаются заглавными буквами A,B,M,N., а элементы обозначают прописными буквами: a,b,x,y. Если некоторый элемент x принадлежит множеству А, то пишут x 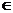 A. Если x не принадлежит А, то пишут x
A. Если x не принадлежит А, то пишут x  A или x
A или x  A.
A.
Например, 5ÎN;  ÎQ;
ÎQ; 
 Q; 0
Q; 0  N.
N.
Два множества А и В называются равными в том и только том случае, когда каждый элемент множества А является элементом множества В и, наоборот, каждый элемент множества В является элементом множества А. Это значит, что множество однозначно определяется своими элементами. Если множество А равно множеству В, то пишут А=В.
Если каждый элемент множества В является элементом множества А, то говорят, что множество В включается во множество А и пишут: В Ì А, или А É В, где É и Ì значит включение. В этом случае множество В называют подмножеством множества А. Из определения подмножества следует, что включение ВÍА допускает одновременное выполнение условия В=А, а это значит, что в число подмножеств любого множества входит и само это множество. Подмножества множества А, не совпадающие с множеством А, называются собственными подмножествами множества А.
Наконец, два множества А и В равны в том и только том случае, если выполняется система двух вложений А Ì В, В ÉА.
Примеры: N ÌZ, Z ÌQ, Q ÌR, Z0 ÌZ, N ÌZ0..
Введем в рассмотрение пустое множество, т.е. ”множество”, не содержащее ни одного элемента. Пустое множество обозначается символом 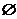 . Пустое множество является подмножеством любого множества. Это следует из определения подмножества как множества, не содержащего элементов, не принадлежащих А..
. Пустое множество является подмножеством любого множества. Это следует из определения подмножества как множества, не содержащего элементов, не принадлежащих А..
Задание множеств.
Существует два способа задания множества: перечислением его элементов и описанием свойств, присущих только элементам данного множества. При первом способе, в фигурных скобках перечисляются элементы, входящие в состав данного множества. Например: A={0;3;–2;4;5;23}, N={1;2;3;..}.
При втором способе также используются фигурные скобки, но теперь внутри скобок проводят вертикальную черту, разделяющую описание множества на две части. Слева от черты указывают, из какого множества объектов выбираются элементы данного множества, а справа описываются свойства, которыми обладают объекты, входящие в состав данного множества. Например, А={xÎN ½0<x<5}={1;2;3;4;…}.
Операции над множествами.
Определение.Объединением множеств А и В называется множество АÈВ, каждый элемент которого принадлежит либо множеству А либо множеству В (либо обоим этим множествам).
Пример. 1) Если А={1;2;3;4}, B={3;4;5;6} и C=AÈB, то С={1;2;3;4;5;6}.
2) Пусть М={xÎR ½xÎ[3; 5]}, P={xÎR½xÎ[4;6) } и T=MÈP. Тогда Т={xÎR½xÎ[3;6)}.
Определение. Пересечением множеств А и В называется множество А ÇВ, каждый элемент которого принадлежит одновременно множествам А и В.
Пример. 1) Если А={1;2;3;4}, B={3;4;5;6} и C=AÇB, то С={3;4}.
2) Пусть М={xÎR ½xÎ[3; 5]}, P={xÎR½xÎ[4;6) } и S=MÇP. Тогда S={xÎR½xÎ[4;5]}.
Если пересечение А и В пусто (АÇВ= 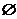 ), то множества А и В называются непересекающимися.
), то множества А и В называются непересекающимися.
Определение. Разностью множеств А и В называется множество А\В, состоящее из тех элементов множества А, которые не принадлежат множеству В.
Пример. Для множеств А, B, M, P, приведенных в предыдущих примерах, будем иметь: A\B={1;2}, M\P=[3;4).
Если множество А рассматривается как подмножество некоторого универсального множества U, то U\A называется дополнением множества А до множества U и обозначается 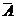 , или символ Сu, т.е.
, или символ Сu, т.е. 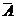 = Сu А.
= Сu А.
Определение.Дизъюнктивной суммой (симметрической разностью) множеств А и В называется множество АÅВ(или АDВ), каждый элемент которого принадлежит либо множеству А, либо множеству В, но не принадлежит одновременно А и В.
Примеры.1. Для приведенных выше множеств А, В, М, Р будем иметь:
АÅВ={1;2;5;6} и MÅP=[3;4)È(5;6).
2. Даны множества А=íxÎZ ï 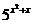 £25ý, В=íxÎR ïx3+4x2+3x=0ý.
£25ý, В=íxÎR ïx3+4x2+3x=0ý.
Найти: AÈB, AÇB, A\B, B\A, ADB.
Решение. 1. Множество A представляет собой совокупность целых чисел, удовлетворяющих условию  £25. Поэтому, чтобы непосредственно указать элементы множества A, решим неравенство. Итак,
£25. Поэтому, чтобы непосредственно указать элементы множества A, решим неравенство. Итак, 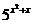 £25,
£25, 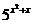 £52.
£52.
Поскольку основание показательной функции больше единицы, то x2+x£2,
(x-1)(x+2)£0. Отсюда получаем, что –2£x£1. Таким образом, A=í-2;-1;0;1ý.
2. Множество В состоит из действительных чисел, являющихся корнями уравнения x3+4x2+3x=0. Следовательно, В={-3;–1;0}
3. Множество AÈB содержит все элементы А и В, и не содержит никаких других элементов, то есть АÈВ={-3;-2;-1;0;1}
4. Множество АÇВ содержит все общие для А и В элементы, т.е. АÇВ={-1;0}.
5. Множество А\В получается удалением из множества А общих с В элементов: А\В={-2;1}.
6.Множество В\А получается удалением из множества В общих с А элементов: В\А={-3}.
7.Множество АDВ содержит все элементы А и В, кроме их общих элементов, то есть
АDВ={-3;-2;1}.
Замечание: Если уже найдены множества А\В,В\А, то для нахождения множества АDВ можно воспользоваться формулой: АDВ=(А\В)È(В\А).
Мощность множества.
Конечные множества можно сравнивать по количеству элементов, содержащихся в них. Для сравнения по насыщенности бесконечных множеств используется принцип сравнения. Между множеством точек гипотенузы прямоугольного треугольника и множеством точек катета можно установить соответствие таким образом, что каждой точке гипотенузы будет соответствовать точка катета и при этом разным точкам гипотенузы соответствуют разные точки катета. Соответствие устанавливается с помощью прямой, проведенной параллельно другому катету через взятую на гипотенузе точку М.
Определение. Говорят, что между элементами А и В установлено взаимно однозначное соответствие, если указано правило, по которому каждому элементу аÎА сопоставлен один элемент вÎВ, называемый образом а, причем выполнены следующие два условия: 1) любые два различные элемента из А имеют различные образы; 2) каждый элемент из В является образом некоторого элемента из А.
Определение. Два множества А и В называются эквивалентными или имеющими одинаковую мощность (обозначается А ~ В), если между их элементами может быть установлено взаимно однозначное соответствие.
Примеры эквивалентных бесконечных множеств:
1. Множество N всех натуральных чисел и множество N1 всех целых отрицательных чисел эквивалентны: nÎN, -nÎN1, N~N1
2. Множество N эквивалентно множеству P положительных четных чисел:
nÎN, 2nÎP, N~P.
3. Множество действительных чисел и множество чисел интервала G=( 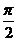 ; -
; - 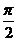 )
)
эквивалентны между собой. Эквивалентность этих множеств легко проверить с помощью соответствия у=tgx (xÎG,yÎR).
4. Любые два отрезка эквивалентны между собой. Взаимно однозначное соответствие между точками отрезков ОА и ОВ устанавливается с помощью прямых,
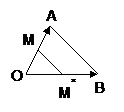 проводимых параллельно отрезку АВ. Способ установления взаимно однозначного соответствия между элементами (точками) показан на рисунке.
проводимых параллельно отрезку АВ. Способ установления взаимно однозначного соответствия между элементами (точками) показан на рисунке.
Два множества, порознь эквивалентные третьему, эквивалентны между собой: Если А~B и B~C, то А~B. Поэтому любой отрезок эквивалентен, например, отрезку [0;1].
Множества, эквивалентные множеству всех вещественных чисел из отрезка [0;1] называют множеством мощности континуум (сокращенно мощности С). Значит, множество чисел любого числового отрезка имеет мощность С. В частности, множество всех вещественных чисел R~( 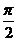 ; -
; - 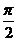 )~[0;1] имеет мощность С.
)~[0;1] имеет мощность С.
Законы алгебры логики.
1а 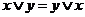 | 1б 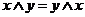 коммутативность коммутативность |
2а 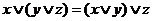 | 2б 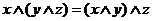 ассоциативность ассоциативность |
3а 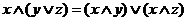 | 3б 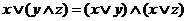 дистрибутивность дистрибутивность |
4а 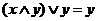 | 4б 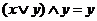 закон поглощения закон поглощения |
5а 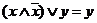 | 5б 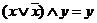 закон Моргана закон Моргана |
Контактные схемы.
Одним из приложений булевых функций является анализ и синтез так называемых контактных схем. Будем рассматривать переключательные схемы электрической цепи.
Между источником питания и потребителем может быть замыкающий и размыкающий цепь контакт, либо цепь контактов, соединенных последовательно или параллельно. Каждому контакту поставим в соответствие логическую переменную, которая примет значение 1, если контакт в рассматриваемый момент времени замыкает цепь, и значение 0, если цепь разомкнута.

Поместим между источником и потребителем тока два контакта, соединенные последовательно (рис. b). Соответствующие им логические переменные обозначим через х1 и х2. Для такой цепи условие прохождения тока описывается конъюнкцией х1Ùх2.
Если контакты соединены параллельно (рис с), то цепь замкнута, когда хотя бы один из контактов замкнут, и разомкнута, когда оба они разомкнуты. Очевидно, работа в цепи в этом случае описывается дизъюнкцией х1Úх2.
Контакты не всегда независимы друг от друга. Можно устроить так, чтобы замыкались и размыкались одновременно. В этом случае контакты называют идентичными и им ставят в соответствие одинаковые логические переменные.
Однако можно устроить так , что при замыкании одного контакта другой размыкается. В этом случае контакты называют инверсными. Любую формулу логики высказываний можно моделировать в виде переключательной схемы.
Пример. Совершенной дизъюнктивной нормальной форме (с.д.н.ф.) F(x,у,z) 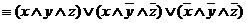 , составленной по таблице истинности, соответствует переключательная схема вида:
, составленной по таблице истинности, соответствует переключательная схема вида:
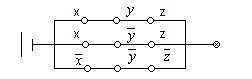
Для соответствующей совершенной конъюнктивной нормальной формы (с.к.н.ф.)
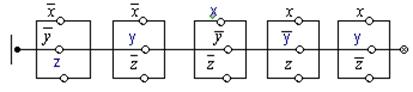 |
F(x,y,z)
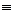
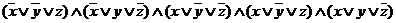 переключательная схема имеет вид:
переключательная схема имеет вид:Векторное произведение.
Определение.Векторным произведением вектора  на вектор
на вектор  называется вектор
называется вектор  , или
, или 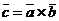 , определяемый следующими тремя условиями:
, определяемый следующими тремя условиями:
1) Модуль вектора  равен
равен  , где
, где  - угол между векторами
- угол между векторами  и
и  , т.е.
, т.е.
l  l=
l=  .
.
Отсюда следует, что модуль векторного произведения численно равен площади параллелограмма, построенного на векторах  и
и  как на сторонах.
как на сторонах.
2) Вектор  перпендикулярен к каждому из векторов
перпендикулярен к каждому из векторов  и
и  (
(  ^
^  ;
;  ^
^  ), т.е. перпендикулярен плоскости параллелограмма, построенного на векторах
), т.е. перпендикулярен плоскости параллелограмма, построенного на векторах  и
и  .
.
3) Вектор  направлен так, что если смотреть из его конца, кратчайший поворот от вектора
направлен так, что если смотреть из его конца, кратчайший поворот от вектора  к вектору
к вектору  был бы против часовой стрелки. (векторы
был бы против часовой стрелки. (векторы  ,
,  ,
,  образуют правую тройку).
образуют правую тройку).
Библиографический список
1. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. М., Наука, 2002.
2. Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. Р., Феникс, 1997.
3. Клетеник Д.В. Сборник задач по аналитической геометрии. М., Наука, 1995.
Оглавление
1. Лекция 1. Множества. 3
2. Лекция 2. Элементы математической логики. 8
3. Задачи на тему “Логика” 11
4. Лекция 3. Векторная алгебра. 12
5.Лекция 4. СКАЛЯРНОЕ, ВЕКТОРНОЕ, СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ. 20
6. Задачи по теме “Векторная алгебра”. 25
АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Учебное пособие
(часть I)
Ростов-на-Дону
УДК 517
Ш31
Ш31 Шевченко Н.П., Смирнова И.Ю. Алгебра и аналитическая геометрия. Учеб. пособие (часть I). Ростов-на-Дону: Издательский центр ДГТУ. 2004. 30с.
Учебное пособие (часть I) представляет собой опорный конспект лекций и упражнений по теме: «Множества, элементы математической логики, векторная алгебра». Рассмотрены основные понятия, свойства, приведены примеры с решениями. Пособие рассчитано на студентов первого курса всех специальностей, изучающих указанные разделы курса Высшая математика.
Печатается по решению редакционно-издательского совета
Донского государственного технического университета.
Научный редактор д.ф.-м. н., проф. А.В. Братищев.
Рецензенты: к. ф.-м. н. Т.Н. Радченко (РГУ, г. Ростов-на-Дону)
©Издательский центр ДГТУ, 2004
Лекция 1. Множества.
Множество-это неопределяемое понятие, смысл которого ясен на основании практической деятельности человека. “Объекты”, входящие в состав множества, называются элементами заданного множества. Множества, элементами которых являются числа, называются числовыми множествами. Стандартные числовые множества:
N-множество натуральных чисел: {1, 2, 3,…},
Z-множество всех целых чисел: {0,  1,
1,  2,…},
2,…},
Z0-множество всех неотрицательных целых чисел: {0, 1, 2, …},
Q-множество рациональных чисел: {  }, m, n
}, m, n 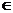 N,
N,
R-множество действительных чисел, I-множество иррациональных чисел
Множества обозначаются заглавными буквами A,B,M,N., а элементы обозначают прописными буквами: a,b,x,y. Если некоторый элемент x принадлежит множеству А, то пишут x 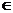 A. Если x не принадлежит А, то пишут x
A. Если x не принадлежит А, то пишут x  A или x
A или x  A.
A.
Например, 5ÎN;  ÎQ;
ÎQ; 
 Q; 0
Q; 0  N.
N.
Два множества А и В называются равными в том и только том случае, когда каждый элемент множества А является элементом множества В и, наоборот, каждый элемент множества В является элементом множества А. Это значит, что множество однозначно определяется своими элементами. Если множество А равно множеству В, то пишут А=В.
Если каждый элемент множества В является элементом множества А, то говорят, что множество В включается во множество А и пишут: В Ì А, или А É В, где É и Ì значит включение. В этом случае множество В называют подмножеством множества А. Из определения подмножества следует, что включение ВÍА допускает одновременное выполнение условия В=А, а это значит, что в число подмножеств любого множества входит и само это множество. Подмножества множества А, не совпадающие с множеством А, называются собственными подмножествами множества А.
Наконец, два множества А и В равны в том и только том случае, если выполняется система двух вложений А Ì В, В ÉА.
Примеры: N ÌZ, Z ÌQ, Q ÌR, Z0 ÌZ, N ÌZ0..
Введем в рассмотрение пустое множество, т.е. ”множество”, не содержащее ни одного элемента. Пустое множество обозначается символом 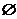 . Пустое множество является подмножеством любого множества. Это следует из определения подмножества как множества, не содержащего элементов, не принадлежащих А..
. Пустое множество является подмножеством любого множества. Это следует из определения подмножества как множества, не содержащего элементов, не принадлежащих А..
Задание множеств.
Существует два способа задания множества: перечислением его элементов и описанием свойств, присущих только элементам данного множества. При первом способе, в фигурных скобках перечисляются элементы, входящие в состав данного множества. Например: A={0;3;–2;4;5;23}, N={1;2;3;..}.
При втором способе также используются фигурные скобки, но теперь внутри скобок проводят вертикальную черту, разделяющую описание множества на две части. Слева от черты указывают, из какого множества объектов выбираются элементы данного множества, а справа описываются свойства, которыми обладают объекты, входящие в состав данного множества. Например, А={xÎN ½0<x<5}={1;2;3;4;…}.
Операции над множествами.
Определение.Объединением множеств А и В называется множество АÈВ, каждый элемент которого принадлежит либо множеству А либо множеству В (либо обоим этим множествам).
Пример. 1) Если А={1;2;3;4}, B={3;4;5;6} и C=AÈB, то С={1;2;3;4;5;6}.
2) Пусть М={xÎR ½xÎ[3; 5]}, P={xÎR½xÎ[4;6) } и T=MÈP. Тогда Т={xÎR½xÎ[3;6)}.
Определение. Пересечением множеств А и В называется множество А ÇВ, каждый элемент которого принадлежит одновременно множествам А и В.
Пример. 1) Если А={1;2;3;4}, B={3;4;5;6} и C=AÇB, то С={3;4}.
2) Пусть М={xÎR ½xÎ[3; 5]}, P={xÎR½xÎ[4;6) } и S=MÇP. Тогда S={xÎR½xÎ[4;5]}.
Если пересечение А и В пусто (АÇВ= 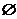 ), то множества А и В называются непересекающимися.
), то множества А и В называются непересекающимися.
Определение. Разностью множеств А и В называется множество А\В, состоящее из тех элементов множества А, которые не принадлежат множеству В.
Пример. Для множеств А, B, M, P, приведенных в предыдущих примерах, будем иметь: A\B={1;2}, M\P=[3;4).
Если множество А рассматривается как подмножество некоторого универсального множества U, то U\A называется дополнением множества А до множества U и обозначается 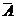 , или символ Сu, т.е.
, или символ Сu, т.е. 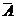 = Сu А.
= Сu А.
Определение.Дизъюнктивной суммой (симметрической разностью) множеств А и В называется множество АÅВ(или АDВ), каждый элемент которого принадлежит либо множеству А, либо множеству В, но не принадлежит одновременно А и В.
Примеры.1. Для приведенных выше множеств А, В, М, Р будем иметь:
АÅВ={1;2;5;6} и MÅP=[3;4)È(5;6).
2. Даны множества А=íxÎZ ï 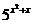 £25ý, В=íxÎR ïx3+4x2+3x=0ý.
£25ý, В=íxÎR ïx3+4x2+3x=0ý.
Найти: AÈB, AÇB, A\B, B\A, ADB.
Решение. 1. Множество A представляет собой совокупность целых чисел, удовлетворяющих условию  £25. Поэтому, чтобы непосредственно указать элементы множества A, решим неравенство. Итак,
£25. Поэтому, чтобы непосредственно указать элементы множества A, решим неравенство. Итак, 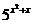 £25,
£25, 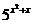 £52.
£52.
Поскольку основание показательной функции больше единицы, то x2+x£2,
(x-1)(x+2)£0. Отсюда получаем, что –2£x£1. Таким образом, A=í-2;-1;0;1ý.
2. Множество В состоит из действительных чисел, являющихся корнями уравнения x3+4x2+3x=0. Следовательно, В={-3;–1;0}
3. Множество AÈB содержит все элементы А и В, и не содержит никаких других элементов, то есть АÈВ={-3;-2;-1;0;1}
4. Множество АÇВ содержит все общие для А и В элементы, т.е. АÇВ={-1;0}.
5. Множество А\В получается удалением из множества А общих с В элементов: А\В={-2;1}.
6.Множество В\А получается удалением из множества В общих с А элементов: В\А={-3}.
7.Множество АDВ содержит все элементы А и В, кроме их общих элементов, то есть
АDВ={-3;-2;1}.
Замечание: Если уже найдены множества А\В,В\А, то для нахождения множества АDВ можно воспользоваться формулой: АDВ=(А\В)È(В\А).
