Процес ортогализ (определен орто)
Норма вектора
Скколяр произвед
Евклид простр
Ортоганализ
Процес ортогализ (определен орто)
Метод грама- шмидта
Норма вектора
Для обозначения длины (называемой также нормой вектора) используется обозначение 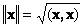 .
.
Например,  .
.
Вектор единичной длины (||x|| = 1) называется нормированным. Ненулевой вектор (x ≠ 0) можно нормировать, разделив его на длину, т.е. x = ||x|| (x/||x||) = ||x|| e.
Здесь e = x/||x|| — нормированный вектор.
Векторы называются ортонормированными, если все они нормированы и попарно ортогональны.
Скалярное произведение вектора самого на себя называется скалярным квадратом. Эта величина 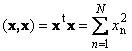 определяет квадрат длины вектора x.
определяет квадрат длины вектора x.
Скалярное произведение
Кроме операций сложения и умножения на число на множестве векторов определены еще несколько операций. Одна из них -- скалярное произведение, позволяющее находить длины векторов и углы между векторами по координатам векторов.
Определение. Скалярным произведением векторов a и b называется число, равноепроизведению длин этих векторов и косинуса угла между ними 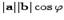 , где
, где 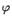 -- угол между векторами a и b.
-- угол между векторами a и b.
Замечание. Если один из векторов нулевой, то угол 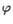 не определен. Скалярное произведение в этом случае считается равным нулю.
не определен. Скалярное произведение в этом случае считается равным нулю.
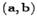 Скалярное произведение обозначается
Скалярное произведение обозначается 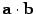 , или
, или 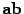 , или . Скалярное произведение вектора на себя, aa, обозначается
, или . Скалярное произведение вектора на себя, aa, обозначается 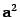 . Скалярное произведение обладает следующими свойствами:
. Скалярное произведение обладает следующими свойствами:
Теорема.Для любых векторов a и b выполнены следующие соотношения:
1) 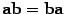 , свойство коммутативности;
, свойство коммутативности;
2) (aа, b) = a(а, b), (a — скаляр)
3) (a, b + c)= (a, b) + (а, с),
4) 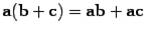 , свойство дистрибутивности;
, свойство дистрибутивности;
5) 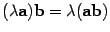 ;
;
6) (a, a) > 0 при 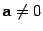 и (а, а) = 0, если а = 0;
и (а, а) = 0, если а = 0;
7) 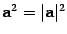 ;
;
8) Если 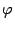 -- угол между векторами a и b, то
-- угол между векторами a и b, то 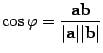 ;
;
9) 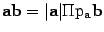 , если
, если 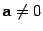 ;
;
10) 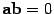 тогда и только тогда, когда векторы a и b ортогональны.
тогда и только тогда, когда векторы a и b ортогональны.
Длина вектора а равна 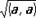 . Если (а, b) = 0, то либо а = 0, либо b = 0, либо a ^ b. Если а = (a1, a2, a3) и b = (b1, b2, b3), то (а, b) = a1 b1 + a2b2 + a3b3 (в прямоугольных декартовых координатах).
. Если (а, b) = 0, то либо а = 0, либо b = 0, либо a ^ b. Если а = (a1, a2, a3) и b = (b1, b2, b3), то (а, b) = a1 b1 + a2b2 + a3b3 (в прямоугольных декартовых координатах).
Понятие "С. п." обобщают на n-мерные векторные пространства, где равенство (а, b) = 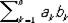 принимают за определение С. и. и с помощью так определённого С. п. вводят геометрическое понятия длины вектора, угла между векторами и т. д. Бесконечномерное линейное пространство, в котором определено С. п. и выполнена аксиома полноты относительно нормы
принимают за определение С. и. и с помощью так определённого С. п. вводят геометрическое понятия длины вектора, угла между векторами и т. д. Бесконечномерное линейное пространство, в котором определено С. п. и выполнена аксиома полноты относительно нормы 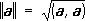 , называют гильбертовым пространством. Гильбертовы пространства играют важную роль в функциональном анализе и квантовой механике.
, называют гильбертовым пространством. Гильбертовы пространства играют важную роль в функциональном анализе и квантовой механике.
Так как 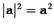 , если
, если 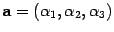 , то
, то 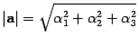 . Пусть в пространстве заданы точки
. Пусть в пространстве заданы точки 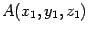 и
и 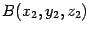 . Тогда
. Тогда 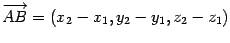 . Длина отрезка
. Длина отрезка 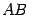 , то есть расстояние между точками
, то есть расстояние между точками 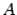 и
и 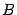 , будет равна
, будет равна 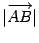 , получим
, получим 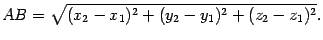
Задача. Даны вершины треугольника: 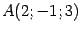 ,
, 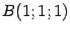 ,
, 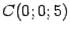 . Найдите длину стороны
. Найдите длину стороны 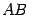 и
и 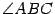 .
.
Решение. 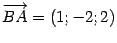 ,
, 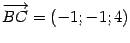 ,
, 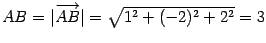 .
.
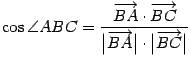 ,
, 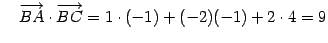 ,
, 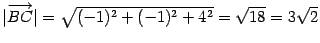 ,
, 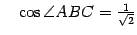 ,
, 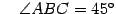 .
.
Ответ: 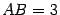 ,
, 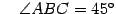 .
.
Задача. Определить длины диагоналей параллелограмма, построенного на векторах 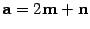 и
и 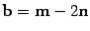 , где m и n -- единичные векторы, угол между которыми равен
, где m и n -- единичные векторы, угол между которыми равен 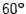 .
.
Решение. В этой задаче не заданы координаты векторов в ортонормированном базисе 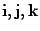 . Поэтому воспользоваться формулами так просто не получится.
. Поэтому воспользоваться формулами так просто не получится.
Сделав схематический рисунок
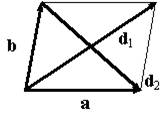
убеждаемся, что вектор 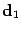 , соответствующий одной диагонали параллелограмма, находится по формуле
, соответствующий одной диагонали параллелограмма, находится по формуле 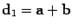 , а другой --
, а другой -- 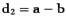 . Отсюда
. Отсюда 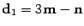 и
и 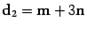 . В силу свойства скалярного произведения получим
. В силу свойства скалярного произведения получим 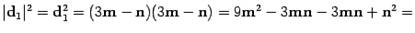
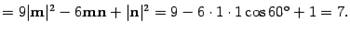
Аналогично, 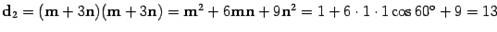 .
.
Ответ: 7 и 13.
Евклидовы пространства
В аналитической геометрии последовательность кажется более «естественной»: скалярное произведение двух векторов 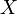 и
и 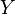 определялось как произведение длин этих векторов на косинус угла между ними:
определялось как произведение длин этих векторов на косинус угла между ними: 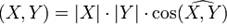 . Тем не менее, формально непротиворечива и обратная схема: если допустить, что скалярное произведение любых двух векторов может быть как-то вычислено (например, в
. Тем не менее, формально непротиворечива и обратная схема: если допустить, что скалярное произведение любых двух векторов может быть как-то вычислено (например, в 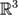 по формуле
по формуле 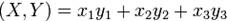 при заданных прямоугольных координатах
при заданных прямоугольных координатах 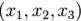 и
и 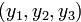 векторов
векторов 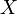 и
и 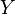 ), то и длину векторов и угол между ними можно выразить через подходящие скалярные произведения:
), то и длину векторов и угол между ними можно выразить через подходящие скалярные произведения: 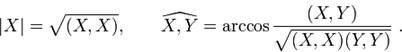
Определения
1 Линейное пространство 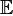 называется евклидовым, если в этом пространстве определена операция, ставящая в соответствие паре векторов
называется евклидовым, если в этом пространстве определена операция, ставящая в соответствие паре векторов 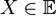 и
и 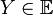 вещественное число, называемое скалярным произведением векторов
вещественное число, называемое скалярным произведением векторов 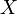 и
и 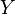 , и обозначаемое
, и обозначаемое 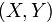 ; при этом операция подчиняется аксиомам:
; при этом операция подчиняется аксиомам:
1 Вещественное линейное пространство E называется евклидовым, если в нём определена операция скалярного умножения: любым двум элементам x , y 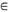 E сопоставлено вещественное число (x, y) =α, удовлетворяющее следующим требованиям,
E сопоставлено вещественное число (x, y) =α, удовлетворяющее следующим требованиям,
каковы бы ни были элементы x , y , z 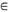 L и число α
L и число α 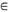 R:
R:
1. (x, y) = (y , x) ;
2. (x + y, z) = ((x, z) + (y, z));
3. (α x, y) = (x, α y) =α (x ,y) ;
4. (x, x ) >0 для всех x≠0 ;
5. (x, x) = 0 , если x = 0.
1. 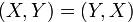 для
для 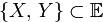 ;
;
2. 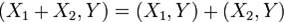 для
для 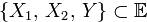 ;
;
3. 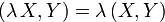 для
для 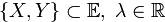 ;
;
4. 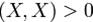 для
для 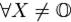 ,
, 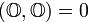 .
.
Из аксиом 1 и 2 вытекает свойство линейности скалярного произведения и по второму вектору:
2'. 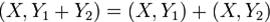 для
для 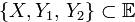 .
.
Определение 2. Вещественное линейное пространство E называется евклидовым, если в нём задана положительно определённая квадратичная форма. В произвольном линейном пространстве существует бесконечно много положительно определённых квадратичных форм. Во втором определении слово “задана” означает, что одна из квадратичных форм выделена и играет особую роль (играет роль выбора масштаба измерения). Будем называть эту выделенную положительно определенную квадратичную форму основной квадратичной формой.
Любое подпространство E’ - также является евклидовым пространством, так как для его элементов определено то же самое скалярное умножение.
Примеры евклидовых пространств.
Пример 1. Геометрические векторы на плоскости L2 и в пространстве L3 с заданным скалярным произведением
Образуют, соответствующие евклидовы пространства.
Пример 2. В арифметическом пространстве Rn мы можем ввести для элементов
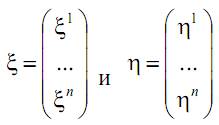
Число 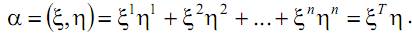
Используя свойства умножения матриц легко можно проверить выполнение всех аксиом из определения 1.
Иначе можно сказать, что в качестве основной квадратичной формы выбрана та, которая в стандартном базисе арифметического пространства (состоящем из столбцов единичной матрицы порядка n ) имеет канонический вид.
Пример 3. В пространстве функций, непрерывных на отрезке [a, b], можно ввести скалярное произведение по формуле 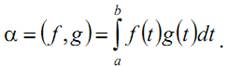
Аксиомы 1-5 вытекают из известных свойств определённых интегралов.
Определение. Длиной вектора x в евклидовом пространстве Eмы будем называть величину 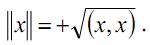
В арифметическом пространстве Rn длина элемента ξ определена как 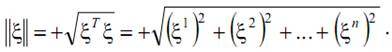
В пространстве функций, непрерывных на отрезке[a,b], длина элемента f (t) равна 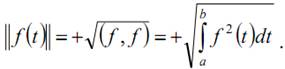
Чтобы избежать выражения “длина функции” 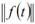 часто называют нормой функции f (t) на отрезке [a,b].
часто называют нормой функции f (t) на отрезке [a,b].
Пример 4. Пространство 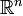 .
.
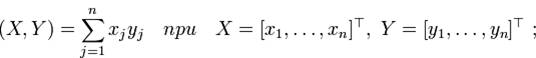
здесь векторы 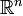 рассматриваются как столбцы, а
рассматриваются как столбцы, а  означает транспонирование. Легко проверить выполнимость аксиом 1 - 4 . Однако определение скалярного произведения последней формулой вовсе не является единственно допустимым; формально скалярное произведение можно ввести и другим способом. Рассмотрим (пока произвольную) вещественную квадратную матрицу А порядка n :
означает транспонирование. Легко проверить выполнимость аксиом 1 - 4 . Однако определение скалярного произведения последней формулой вовсе не является единственно допустимым; формально скалярное произведение можно ввести и другим способом. Рассмотрим (пока произвольную) вещественную квадратную матрицу А порядка n :
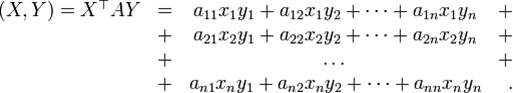
(Здесь векторы 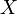 и
и 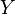 из
из 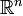 снова рассматриваются как столбцы.) Если матрица A является положительно определенной, то все аксиомы скалярного произведения будут удовлетворены.
снова рассматриваются как столбцы.) Если матрица A является положительно определенной, то все аксиомы скалярного произведения будут удовлетворены.
Квадратная матрица A называется положительно определенной, если для любого ненулевого вектора x ≠ 0, справедливо (A*X)*XT > 0.
Докажем по определению положительную определённость матрицы A

Докажем, что для для всех x ≠ 0, x ∈ E3 произведение xTAx положительно:
xTAx > 0:
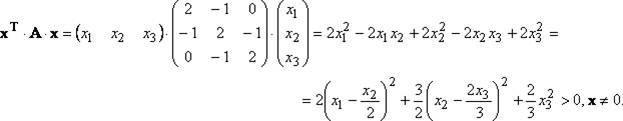
Если A — это квадратная матрица, а x и y — вектора соответствующей размерности, то скалярное произведение вида XTAy называется билинейной формой , определяемой матрицей A. При x=y выражение XTAx называется квадратичной формой.
Пример 5. Линейное пространство квадратных матриц порядкаn с вещественными элементами. Скалярное произведение введем формулой 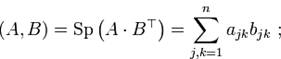
Здесь 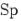 означает след матрицы, т.е. сумму элементов ее главной диагонали.
означает след матрицы, т.е. сумму элементов ее главной диагонали.
На основании аксиом скалярного произведения, его вычисление для произвольных векторов 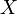 и
и 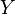 может быть сведено к вычислению скалярных произведений векторов произвольного базиса. В самом деле, если система
может быть сведено к вычислению скалярных произведений векторов произвольного базиса. В самом деле, если система 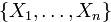 составляет базис пространства
составляет базис пространства 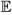 , то, разложив оба вектора по этому базису
, то, разложив оба вектора по этому базису
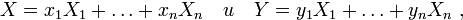
получаем: 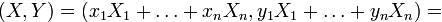
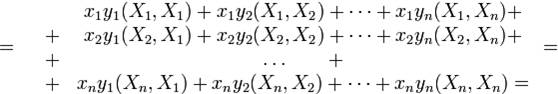
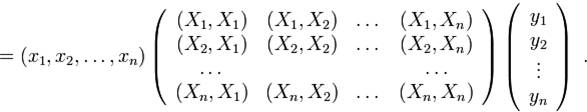
Итак, при изменении векторов 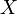 и
и 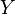 в последней формуле изменятся лишь строка и столбец координат, а промежуточная матрица останется неизменной. Задание этой матрицы, следовательно, полностью определит скалярное произведение в
в последней формуле изменятся лишь строка и столбец координат, а промежуточная матрица останется неизменной. Задание этой матрицы, следовательно, полностью определит скалярное произведение в 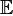 . Фактически задание скалярного произведения в разобранном выше примере пространства
. Фактически задание скалярного произведения в разобранном выше примере пространства 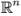 по формуле
по формуле 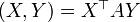 можно рассматривать именно как частный случай этого при подходящем подборе базисных векторов. Согласно рассуждениям из примера 1, матрица
можно рассматривать именно как частный случай этого при подходящем подборе базисных векторов. Согласно рассуждениям из примера 1, матрица 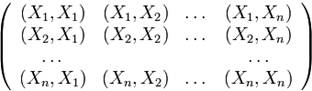 должна обладать некоторыми принципиальными свойствами. Так оно и окажется.
должна обладать некоторыми принципиальными свойствами. Так оно и окажется.
Матрицей Грама системы векторов 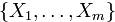 называется квадратная матрица
называется квадратная матрица
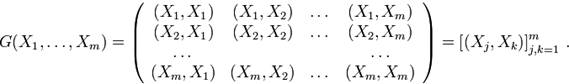
Ее определитель называется определителем Грама (или грамианом) системы векторов 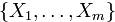 :
: 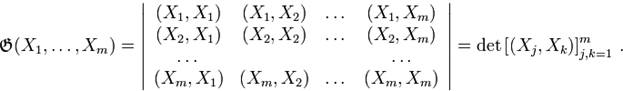
С помощью матрицы Грама формула скалярного произведения записывается в виде 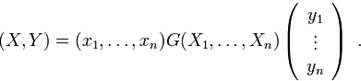
Ортогонализация
Ортогонализация ―алгоритм построения для данной линейно независимой системы векторов евклидова или эрмитова пространства V ортогональной системы ненулевых векторов, порождающих то же самое подпространство в V.
Наиболее известным является процесс Грама ― Шмидта, при котором по линейно независимой системе 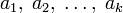 строится ортогональная система
строится ортогональная система 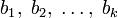 такая, что каждый вектор bi линейно выражается через
такая, что каждый вектор bi линейно выражается через 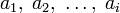 , то есть матрица перехода от {ai} к {bi} ― верхнетреугольная матрица.
, то есть матрица перехода от {ai} к {bi} ― верхнетреугольная матрица.
Алгоритм
Пусть имеются линейно независимые векторы 
Определим оператор проекции следующим образом: 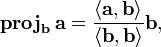
где  — скалярное произведение векторов
— скалярное произведение векторов 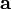 и
и  . Этот оператор проецирует вектор
. Этот оператор проецирует вектор 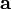 ортогонально на вектор
ортогонально на вектор  .
.
Классический процесс Грама — Шмидта выполняется следующим образом:
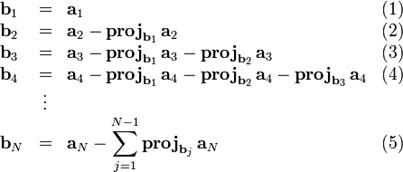
На основе каждого вектора 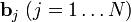 может быть получен нормированный вектор:
может быть получен нормированный вектор: 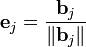 (у нормированного вектора направление будет таким же, как у исходного, а длина — единичной).
(у нормированного вектора направление будет таким же, как у исходного, а длина — единичной).
Результаты процесса Грама — Шмидта:
 — система ортогональных векторов либо
— система ортогональных векторов либо
 — система ортонормированных векторов.
— система ортонормированных векторов.
Вычисление  носит название ортогонализации Грама — Шмидта, а
носит название ортогонализации Грама — Шмидта, а  — ортонормализации Грама — Шмидта.
— ортонормализации Грама — Шмидта.
Геометрическая интерпретация — вариант 1
Рассмотрим формулу (2) — второй шаг алгоритма. Её геометрическое представление изображено на рис. 1:

1 — получение проекции вектора 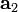 на
на 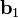 ;
;
2 — вычисление  , то есть перпендикуляра, которым выполняется проецирование конца
, то есть перпендикуляра, которым выполняется проецирование конца 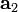 на
на 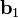 . Этот перпендикуляр — вычисляемый в формуле (2) вектор
. Этот перпендикуляр — вычисляемый в формуле (2) вектор 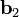 ;
;
3 — перемещение полученного на шаге 2 вектора 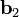 в начало координат. Это перемещение сделано на рисунке лишь для наглядности. Оно не является математическим действием и поэтому не отражается в формуле (2).
в начало координат. Это перемещение сделано на рисунке лишь для наглядности. Оно не является математическим действием и поэтому не отражается в формуле (2).
На рисунке видно, что вектор 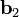 ортогонален вектору
ортогонален вектору 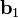 , так как является перпендикуляром, по которому
, так как является перпендикуляром, по которому 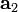 проецируется на
проецируется на 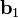 .
.
Рассмотрим формулу (3) — третий шаг алгоритма — в следующем варианте:
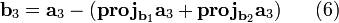
Её геометрическое представление изображено на рис. 2:

1 — получение проекции вектора  на
на 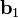 ;
;
2 — получение проекции вектора  на
на 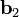 ;
;
3 — вычисление суммы  , то есть проекции вектора
, то есть проекции вектора  на плоскость, образуемую векторами
на плоскость, образуемую векторами 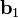 и
и 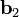 . Эта плоскость закрашена на рисунке серым цветом;
. Эта плоскость закрашена на рисунке серым цветом;
4 — вычисление 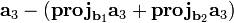 , то есть перпендикуляра, которым выполняется проецирование конца
, то есть перпендикуляра, которым выполняется проецирование конца  на плоскость, образуемую векторами
на плоскость, образуемую векторами 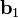 и
и 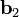 . Этот перпендикуляр — вычисляемый в формуле (6) вектор
. Этот перпендикуляр — вычисляемый в формуле (6) вектор 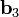 ;
;
5 — перемещение полученного 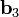 в начало координат. Это перемещение сделано на рисунке лишь для наглядности. Оно не является математическим действием и поэтому не отражается в формуле (6).
в начало координат. Это перемещение сделано на рисунке лишь для наглядности. Оно не является математическим действием и поэтому не отражается в формуле (6).
На рисунке видно, что вектор 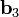 ортогонален векторам
ортогонален векторам 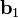 и
и 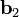 , так как
, так как 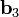 является перпендикуляром, по которому
является перпендикуляром, по которому  проецируется на плоскость, образуемую векторами
проецируется на плоскость, образуемую векторами 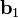 и
и 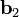 .
.
Таким образом, в процессе Грама — Шмидта для вычисления  выполняется проецирование
выполняется проецирование  ортогонально на гиперплоскость, формируемую векторами
ортогонально на гиперплоскость, формируемую векторами  . Вектор
. Вектор  затем вычисляется как разность между
затем вычисляется как разность между  и его проекцией. То есть
и его проекцией. То есть  — это перпендикуляр от конца
— это перпендикуляр от конца  к гиперплоскости, формируемой векторами
к гиперплоскости, формируемой векторами  . Поэтому
. Поэтому  ортогонален векторам, образующим эту гиперплоскость.
ортогонален векторам, образующим эту гиперплоскость.
Геометрическая интерпретация — вариант 2
Рассмотрим проекции некоторого вектора 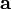 на вектора
на вектора 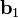 и
и 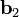 как компоненты вектора
как компоненты вектора 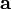 в направлениях
в направлениях 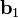 и
и 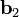 (рис. 3)
(рис. 3)

Если удалить из 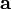 компоненту в направлении
компоненту в направлении 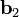 , то
, то 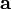 станет ортогонален
станет ортогонален 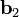 (рис. 4):
(рис. 4):

Если из 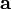 удалить компоненты в направлениях
удалить компоненты в направлениях 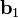 и
и 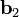 , то станет ортогонален и
, то станет ортогонален и 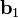 , и
, и 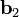 (рис. 5):
(рис. 5):

В формуле (2) из вектора 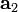 удаляется компонента в направлении вектора
удаляется компонента в направлении вектора 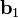 . Получаемый вектор
. Получаемый вектор 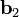 не содержит компоненту в направлении
не содержит компоненту в направлении 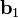 и поэтому ортогонален вектору
и поэтому ортогонален вектору 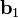 .
.
В формуле (3) из вектора  удаляются компоненты в направлениях
удаляются компоненты в направлениях 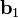 и
и 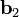 (формуле 3 соответствует переход от рис. 3 к рис. 5; рис. 4 не соответствует формуле 3). Получаемый вектор
(формуле 3 соответствует переход от рис. 3 к рис. 5; рис. 4 не соответствует формуле 3). Получаемый вектор 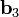 ортогонален векторам
ортогонален векторам 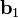 и
и 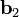 .
.
В формуле (4) из вектора  удаляются компоненты в направлениях
удаляются компоненты в направлениях 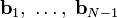 . Получаемый вектор
. Получаемый вектор  ортогонален векторам
ортогонален векторам 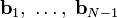 .
.
Таким образом, по формулам (1) — (4) на основе векторов  получается набор ортогональных векторов
получается набор ортогональных векторов  .
.
Численная неустойчивость
При вычислении на ЭВМ по формулам (1) — (5) вектора 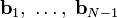 часто не точно ортогональны из-за ошибок округления. Из-за потери ортогональности в процессе вычислений классический процесс Грама — Шмидта называют численно неустойчивым.
часто не точно ортогональны из-за ошибок округления. Из-за потери ортогональности в процессе вычислений классический процесс Грама — Шмидта называют численно неустойчивым.
Особые случаи
Процесс Грама — Шмидта может применяться также к бесконечной последовательности линейно независимых векторов.
Кроме того, процесс Грама — Шмидта может применяться к линейно зависимым векторам. В этом случае он выдаёт 0 (нулевой вектор) на шаге j, если  является линейной комбинацией векторов
является линейной комбинацией векторов 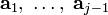 . Если это может случиться, то для сохранения ортогональности выходных векторов и для предотвращения деления на ноль при ортонормировании алгоритм должен делать проверку на нулевые вектора и отбрасывать их. Количество векторов, выдаваемых алгоритмом, будет равно размерности подпространства, порождённого векторами (т.е. количеству линейно независимых векторов, которые можно выделить среди исходных векторов).
. Если это может случиться, то для сохранения ортогональности выходных векторов и для предотвращения деления на ноль при ортонормировании алгоритм должен делать проверку на нулевые вектора и отбрасывать их. Количество векторов, выдаваемых алгоритмом, будет равно размерности подпространства, порождённого векторами (т.е. количеству линейно независимых векторов, которые можно выделить среди исходных векторов).
Норма вектора
Скколяр произвед
Евклид простр
Ортоганализ
Процес ортогализ (определен орто)
Метод грама- шмидта
Норма вектора
Для обозначения длины (называемой также нормой вектора) используется обозначение 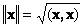 .
.
Например,  .
.
Вектор единичной длины (||x|| = 1) называется нормированным. Ненулевой вектор (x ≠ 0) можно нормировать, разделив его на длину, т.е. x = ||x|| (x/||x||) = ||x|| e.
Здесь e = x/||x|| — нормированный вектор.
Векторы называются ортонормированными, если все они нормированы и попарно ортогональны.
Скалярное произведение вектора самого на себя называется скалярным квадратом. Эта величина 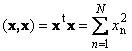 определяет квадрат длины вектора x.
определяет квадрат длины вектора x.
Скалярное произведение
Кроме операций сложения и умножения на число на множестве векторов определены еще несколько операций. Одна из них -- скалярное произведение, позволяющее находить длины векторов и углы между векторами по координатам векторов.
Определение. Скалярным произведением векторов a и b называется число, равноепроизведению длин этих векторов и косинуса угла между ними 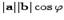 , где
, где 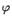 -- угол между векторами a и b.
-- угол между векторами a и b.
Замечание. Если один из векторов нулевой, то угол 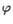 не определен. Скалярное произведение в этом случае считается равным нулю.
не определен. Скалярное произведение в этом случае считается равным нулю.
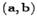 Скалярное произведение обозначается
Скалярное произведение обозначается 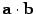 , или
, или 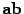 , или . Скалярное произведение вектора на себя, aa, обозначается
, или . Скалярное произведение вектора на себя, aa, обозначается 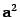 . Скалярное произведение обладает следующими свойствами:
. Скалярное произведение обладает следующими свойствами:
Теорема.Для любых векторов a и b выполнены следующие соотношения:
1) 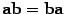 , свойство коммутативности;
, свойство коммутативности;
2) (aа, b) = a(а, b), (a — скаляр)
3) (a, b + c)= (a, b) + (а, с),
4) 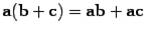 , свойство дистрибутивности;
, свойство дистрибутивности;
5) 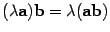 ;
;
6) (a, a) > 0 при 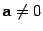 и (а, а) = 0, если а = 0;
и (а, а) = 0, если а = 0;
7) 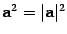 ;
;
8) Если 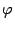 -- угол между векторами a и b, то
-- угол между векторами a и b, то 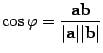 ;
;
9) 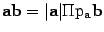 , если
, если 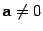 ;
;
10) 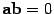 тогда и только тогда, когда векторы a и b ортогональны.
тогда и только тогда, когда векторы a и b ортогональны.
Длина вектора а равна 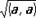 . Если (а, b) = 0, то либо а = 0, либо b = 0, либо a ^ b. Если а = (a1, a2, a3) и b = (b1, b2, b3), то (а, b) = a1 b1 + a2b2 + a3b3 (в прямоугольных декартовых координатах).
. Если (а, b) = 0, то либо а = 0, либо b = 0, либо a ^ b. Если а = (a1, a2, a3) и b = (b1, b2, b3), то (а, b) = a1 b1 + a2b2 + a3b3 (в прямоугольных декартовых координатах).
Понятие "С. п." обобщают на n-мерные векторные пространства, где равенство (а, b) = 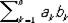 принимают за определение С. и. и с помощью так определённого С. п. вводят геометрическое понятия длины вектора, угла между векторами и т. д. Бесконечномерное линейное пространство, в котором определено С. п. и выполнена аксиома полноты относительно нормы
принимают за определение С. и. и с помощью так определённого С. п. вводят геометрическое понятия длины вектора, угла между векторами и т. д. Бесконечномерное линейное пространство, в котором определено С. п. и выполнена аксиома полноты относительно нормы 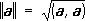 , называют гильбертовым пространством. Гильбертовы пространства играют важную роль в функциональном анализе и квантовой механике.
, называют гильбертовым пространством. Гильбертовы пространства играют важную роль в функциональном анализе и квантовой механике.
Так как 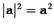 , если
, если 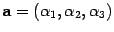 , то
, то 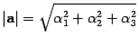 . Пусть в пространстве заданы точки
. Пусть в пространстве заданы точки 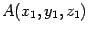 и
и 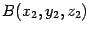 . Тогда
. Тогда 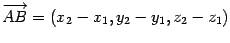 . Длина отрезка
. Длина отрезка 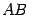 , то есть расстояние между точками
, то есть расстояние между точками 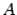 и
и 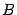 , будет равна
, будет равна 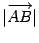 , получим
, получим 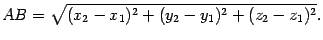
Задача. Даны вершины треугольника: 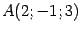 ,
, 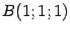 ,
, 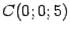 . Найдите длину стороны
. Найдите длину стороны 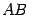 и
и 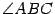 .
.
Решение. 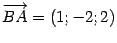 ,
, 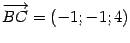 ,
, 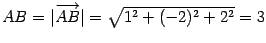 .
.
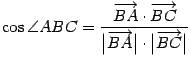 ,
, 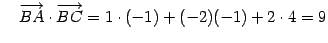 ,
, 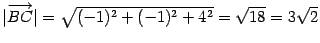 ,
, 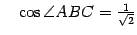 ,
, 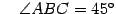 .
.
Ответ: 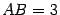 ,
, 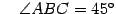 .
.
Задача. Определить длины диагоналей параллелограмма, построенного на векторах 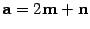 и
и 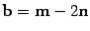 , где m и n -- единичные векторы, угол между которыми равен
, где m и n -- единичные векторы, угол между которыми равен 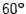 .
.
Решение. В этой задаче не заданы координаты векторов в ортонормированном базисе 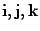 . Поэтому воспользоваться формулами так просто не получится.
. Поэтому воспользоваться формулами так просто не получится.
Сделав схематический рисунок

убеждаемся, что вектор 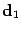 , соответствующий одной диагонали параллелограмма, находится по формуле
, соответствующий одной диагонали параллелограмма, находится по формуле 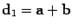 , а другой --
, а другой -- 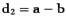 . Отсюда
. Отсюда 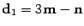 и
и 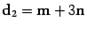 . В силу свойства скалярного произведения получим
. В силу свойства скалярного произведения получим 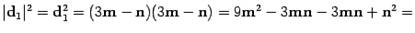
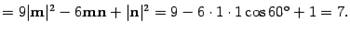
Аналогично, 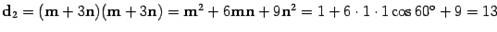 .
.
Ответ: 7 и 13.
Евклидовы пространства
В аналитической геометрии последовательность кажется более «естественной»: скалярное произведение двух векторов 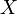 и
и 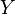 определялось как произведение длин этих векторов на косинус угла между ними:
определялось как произведение длин этих векторов на косинус угла между ними: 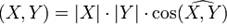 . Тем не менее, формально непротиворечива и обратная схема: если допустить, что скалярное произведение любых двух векторов может быть как-то вычислено (например, в
. Тем не менее, формально непротиворечива и обратная схема: если допустить, что скалярное произведение любых двух векторов может быть как-то вычислено (например, в 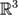 по формуле
по формуле 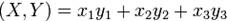 при заданных прямоугольных координатах
при заданных прямоугольных координатах 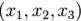 и
и 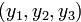 векторов
векторов 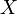 и
и 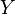 ), то и длину векторов и угол между ними можно выразить через подходящие скалярные произведения:
), то и длину векторов и угол между ними можно выразить через подходящие скалярные произведения: 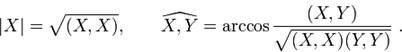
Определения
1 Линейное пространство 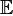 называется евклидовым, если в этом пространстве определена операция, ставящая в соответствие паре векторов
называется евклидовым, если в этом пространстве определена операция, ставящая в соответствие паре векторов 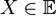 и
и 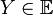 вещественное число, называемое скалярным произведением векторов
вещественное число, называемое скалярным произведением векторов 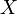 и
и 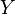 , и обозначаемое
, и обозначаемое 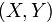 ; при этом операция подчиняется аксиомам:
; при этом операция подчиняется аксиомам:
1 Вещественное линейное пространство E называется евклидовым, если в нём определена операция скалярного умножения: любым двум элементам x , y 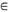 E сопоставлено вещественное число (x, y) =α, удовлетворяющее следующим требованиям,
E сопоставлено вещественное число (x, y) =α, удовлетворяющее следующим требованиям,
каковы бы ни были элементы x , y , z 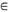 L и число α
L и число α 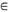 R:
R:
1. (x, y) = (y , x) ;
2. (x + y, z) = ((x, z) + (y, z));
3. (α x, y) = (x, α y) =α (x ,y) ;
4. (x, x ) >0 для всех x≠0 ;
5. (x, x) = 0 , если x = 0.
1. 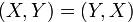 для
для 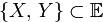 ;
;
2. 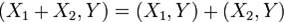 для
для 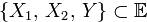 ;
;
3. 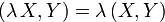 для
для 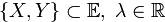 ;
;
4. 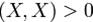 для
для 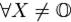 ,
, 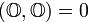 .
.
Из аксиом 1 и 2 вытекает свойство линейности скалярного произведения и по второму вектору:
2'. 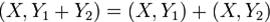 для
для 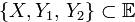 .
.
Определение 2. Вещественное линейное пространство E называется евклидовым, если в нём задана положительно определённая квадратичная форма. В произвольном линейном пространстве существует бесконечно много положительно определённых квадратичных форм. Во втором определении слово “задана” означает, что одна из квадратичных форм выделена и играет особую роль (играет роль выбора масштаба измерения). Будем называть эту выделенную положительно определенную квадратичную форму основной квадратичной формой.
Любое подпространство E’ - также является евклидовым пространством, так как для его элементов определено то же самое скалярное умножение.
Примеры евклидовых пространств.
Пример 1. Геометрические векторы на плоскости L2 и в пространстве L3 с заданным скалярным произведением
Образуют, соответствующие евклидовы пространства.
Пример 2. В арифметическом пространстве Rn мы можем ввести для элементо<
