ТЕМА: Законы динамики. Дифференциальные уравнения движения материальной точки.

ТЕМА: Законы динамики. Дифференциальные уравнения движения материальной точки.

Напоминаю, что объектом изучения статики являлось абсолютно твердое тело, находящееся в состоянии равновесия.

В кинематике мы изучали движение материальных объектов с геометрической точки зрения без учета масс и действующих на них сил.

Но не рассматривали, почему, то или иное тело так движется.

А теперь мы приступаем к изучению динамики, будем рассматривать движение, но уже с учетом действующих сил.

Динамика последний раздел курса теоретической механики. В этом разделе

Решаются самые общие задачи движения материального объекта.

Как и в кинематике, динамику подразделяют на два больших раздела:

- динамику материальной точки;

- динамику системы материальных точек и материального тела.

Начнем мы с изучения движения материальной точки, а затем уже перейдем к системе МТ.

Формулировка.

Динамика ― раздел теоретической механики, в котором движение изучается в зависимости от действующих сил и начального состояния.

В динамике будут решаться уравнения второго порядка и основные действия, которые необходимо будет выполнять - интегрирование

1. Основные законы динамики.

В основе динамики лежат известные вам законы Ньютона и изложенные им на латинском языке в трактате"Математические начала натуральной философии" (1687).

Сочинение Ньютона переведено на русский язык академиком А.Н.Крыловым (Известия морской академии, 1915; перепечатано в Собрании трудов акад. А.Н.Крылова, т. VII изд. АН СССР, 1936)

Законы Ньютона справедливы для тела, которое представляет собой свободную материальную точку.

Первый закон (закон инерции).

Формулировка

Изолированная от внешних воздействий материальная точка сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока приложенная сила не заставит её изменить это состояние.

Второй закон (основной закон динамики).

Во втором законе пойдет речь о зависимости между действующей силой приложенной к точке и ускорением.

В инерциальной системе отсчёта наиболее просто выполняется зависимость между действующей на материальную точку силой и вызываемым ее ускорением:

(1)

Формулировка

Свойство материальной точки реагировать на внешнее воздействие, в результате которого она приобретает соответствующее ускорение, и оказывать при этом сопротивление изменению своей скорости, называется инертностью.

Количественной мерой инертности - является её масса.

Для того чтобы возникло ускорение необходимо внешнее воздействие.

Формула (1) устанавливает причинно-следственную связь.

Третий закон (закон равенства действия и противодействия).

Формулировка

Силы, с которыми две материальные точки действуют друг на друга, всегда равны по модулю и направлены по одной прямой в противоположные стороны.

Данный закон относится не к одной материальной точке, а к системе из двух точек.

Всегда силы возникают попарно. Нет односторонне действующих сил.

Одну из сил взаимодействия двух материальных точек принято называть«действием», а другую ¾ «противодействием».

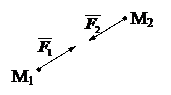Данный закон кратко формулируют следующим образом:

Замечание 1

Первый и второй законы выполняются в инерциальной системе отсчета.

Замечание 2

Формулировка

Всякую несвободную материальную точку, находящуюся в любом движении, можно освободить от связей, заменив действия связей их реакциями, и рассматривать её как свободную, находящуюся под действием приложенных активных сил и реакций связей.

Этот закон называют также принципом освобождаемости от связей.

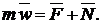(6)

Где

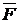- равнодействующая всех активных сил,

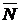равнодействующая всех реакций связей,

Формула (6) выражает основноеуравнение движения несвободной материальной точки

Точки.

Для того, чтобы описать движение материального объекта находящегося под действием сил, необходимо составлять дифференциальные уравнения, а потом их решать.

Решение дифференциальных уравнений называется интегрированием дифференциальных уравнений.

Как известно из кинематики, движение точки математически можно описать тремя способами: векторным, координатным естественным.

Соответственно, из второго закона Ньютона следуют дифференциальные уравнения движения материальной точки ввекторной, в координатной в естественной формах.

Векторная форма

Рассмотрим свободную материальную точку 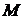массы 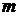, движущуюся под действием системы сил 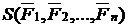относительно инерциальной системы отсчёта

Исходным уравнением является основной закон динамики :

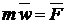. (1)

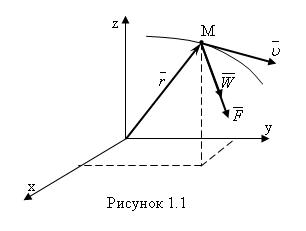
Изображаем координатную систему Оxyz – это инерциальная система отсчета, принято называть движение по отношению к инерциальной системе отсчета абсолютным движением.

Изобразим точку М и силу .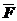

Если посмотреть на первое уравнение, то чем отличается вектор силы от вектора ускорения в скалярной величине?

Скаляром массы.

Значит в этом случае сила и ускорение направлено по одной прямой.

Если воспользоваться формулой

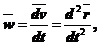
где 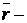радиус – вектор точки, то уравнение (1) принимает вид

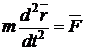(7)

Уравнение (7) называется дифференциальным уравнением движениясвободной материальной точки в векторной форме.

Для несвободной точки в правой части появится, кроме активной силы реакция.

Записываем.

Для несвободной точки уравнение (6) записывается:

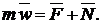
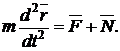(8)

Где

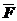- равнодействующая всех активных сил

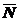- равнодействующая всех реакций связи

Движения самой точки.

Поэтому реакция 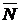заранее неизвестна.

Пример.

Рассмотрим движение груза M, подвешенного к нижнему концу гибкой нерастяжимой нити длиною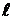

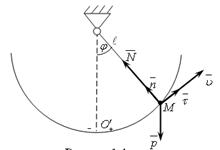
Уравнения (13) в данном случае имеют вид

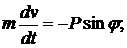
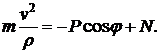
Откуда получаем

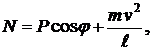
то есть реакция зависит от силы тяжести P, а также от положения точки на траектории, характеризуемого углом 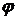, и её скорости 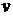в рассматриваемый момент времени.

Адача

Материальная точка массой m движется согласно уравнениям

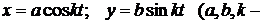постоянные).

Определить силу, вызывающую заданное движение точки. (модуль и направление)

Решение.

Воспользуемся следующими уравнениями:

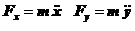
Определим вид траектории.

В кинематике мы рассматривали подобную задачу? Да.

Траекторией точки является эллипс

Находим проекции ускореий на координатные оси.

,

т.к

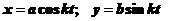
то данные уравнеия можно записать в другом виде

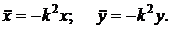
Отличие уравнений состоит в том, что в превом случае мы видим в чему равны производные в любой момент времени, а во втором случае в любом положении точки.

Следовательно проекции силы на оси координат будут равны:

,

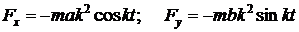или

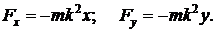
Откуда

таким образом

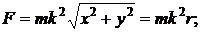
где

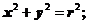
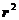- модуль радиуса вектора.

Сила действующая на точку , 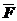– переменная, пропорциональная первой степени растояния до точки О начала координат.

Определим как она направленна.

Силу 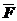предстовляем в виде:

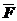= F_X + F_У

Подставляем

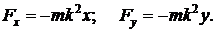в данную формулу и получаем

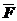= - mk²(x + у )

так как

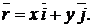
Итак

Чем отличается вектор силы от радиуса вектора?

Знаком и скаляром.

Сила 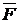в любом положении точки на эллипсе направлена в противоположную сторону вектора 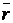, то есть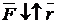

Таким образом, действующая на точку сила пропорциональна расстоянию точки от центра O , и её линия действия в любой момент движения проходит через неподвижный центр O.

Такая сила называется центральной силой. (она линейная ,т.к. пропорциональна первй степени радиуса вектора)

Формулировка.

Вторая основная (обратная) задача.

В случае несвободной материальной точки, во второй основной задаче динамики, требуется по заданным массе, активной силе, начальному положению и начальной скорости точки определить движение точки и реакцию связей .

Какая задача более сложная для свободной, или не свободной?

Эта задача для несвободной материальной точки принципиально отличается от подобной задачи для свободной материальной точки.

При решении второй основной задачи динамики для свободной точки главное правильно составить дифференциальные уравнения движения, после чего их всегда можно проинтегрировать точно или приближёнными способами, известными из теории дифференциальных уравнений.

Для несвободной точки, мы не можем приступить непосредственно к интегрированию ДУ.

Дело в том, что в эти уравнения входят шесть неизвестных: три координаты x, y, z точки и три проекции N_x, N_y, N_z силы реакции 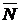, которая зависит не только от вида связи и активной силы 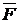, но и от самого движения точки. Поэтому прежде всего нужно каким бы то ни было способом исключить эту реакцию и только после этого можно приступить к интегрированию дифференциальных уравнений, уже не содержащих неизвестную реакцию, а затем по найденным уравнениям движения

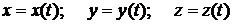
можно легко найти N_x, N_y, N_z

РС

При решении задач все силы можно разделить на силы зависящие от положения, скорости и времени.

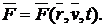
Примерами сил, зависящих от положения точки, являются упругая сила пружины, силы всемирного тяготения, кулоновы силы взаимодействия между зарядами.

К силам, зависящим от скорости, относятся силы сопротивления различных сред.

Сила, вызывающая колебания неуравновешенного мотора на упругом основании, служит примером силы, являющейся периодической функцией времени. К этому же классу сил относятся гидродинамические силы, действующие на винт корабля.

ТЕМА: Законы динамики. Дифференциальные уравнения движения материальной точки.

Напоминаю, что объектом изучения статики являлось абсолютно твердое тело, находящееся в состоянии равновесия.

В кинематике мы изучали движение материальных объектов с геометрической точки зрения без учета масс и действующих на них сил.

Но не рассматривали, почему, то или иное тело так движется.

А теперь мы приступаем к изучению динамики, будем рассматривать движение, но уже с учетом действующих сил.

Динамика последний раздел курса теоретической механики. В этом разделе

Решаются самые общие задачи движения материального объекта.

Как и в кинематике, динамику подразделяют на два больших раздела:

- динамику материальной точки;

- динамику системы материальных точек и материального тела.

Начнем мы с изучения движения материальной точки, а затем уже перейдем к системе МТ.

Формулировка.

Динамика ― раздел теоретической механики, в котором движение изучается в зависимости от действующих сил и начального состояния.

В динамике будут решаться уравнения второго порядка и основные действия, которые необходимо будет выполнять - интегрирование

1. Основные законы динамики.

В основе динамики лежат известные вам законы Ньютона и изложенные им на латинском языке в трактате"Математические начала натуральной философии" (1687).

Сочинение Ньютона переведено на русский язык академиком А.Н.Крыловым (Известия морской академии, 1915; перепечатано в Собрании трудов акад. А.Н.Крылова, т. VII изд. АН СССР, 1936)

Законы Ньютона справедливы для тела, которое представляет собой свободную материальную точку.