Действие шестое.Нахождение обратной матрицы.

Данная тема достаточно обширна, и я вынес данный вопрос на отдельную страницу.

Вычисление определителей

В ходе решения задач по высшей математике очень часто возникает необходимостьвычислить определитель матрицы. Определитель матрицы фигурирует в линейной алгебре, аналитической геометрии, математическом анализе и других разделах высшей математики. Таким образом, без навыка решения определителей просто не обойтись. Также для самопроверки Вы можете бесплатно скачать калькулятор определителей, он сам по себе не научит решать определители, но очень удобен, поскольку всегда выгодно заранее знать правильный ответ!

Я не буду давать строгое математическое определение определителя, и, вообще, буду стараться минимизировать математическую терминологию, большинству читателей легче от этого не станет. Задача данной статьи – научить Вас решать определители второго, третьего и четвертого порядка. Весь материал изложен в простой и доступной форме, и даже полный (пустой) чайник в высшей математике после внимательного изучения материала сможет правильно решать определители.

Определитель можно вычислить только для квадратной матрицы (более подробно см.Действия с матрицами)

На практике чаще всего можно встретить определитель второго порядка, например: 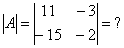, и определитель третьего порядка, например: .

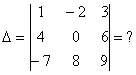Определитель четвертого порядка 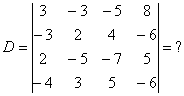встречается значительно реже, но о нем тоже поговорим.

Надеюсь, всем понятно следующее: Числа внутри определителя живут сами по себе, и ни о каком вычитании речи не идет! Менять местами числа нельзя!

(На самом деле, можно переставлять строки и столбцы определителя со сменой (или без смены) знака определителя, но часто в этом нет никакой необходимости)

Таким образом, если дан какой-либо определитель, то ничего внутри него не трогаем!

Обозначения: Если дана матрица 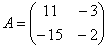, то ее определитель обозначают 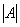. Также очень часто определитель обозначают латинской буквой или греческой .

1) Что значит решить (найти, раскрыть) определитель? Вычислить определитель – это значит НАЙТИ ЧИСЛО. Знаки вопроса 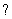в вышерассмотренных примерах – это совершенно обыкновенные числа.

2) Теперь осталось разобраться в том, КАК найти это число. Как Вы догадываетесь, для этого нужно применить определенные правила, формулы и алгоритмы, о чём сейчас и пойдет речь.

Начнем с определителя «два» на «два»:

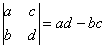
ЭТО НУЖНО ЗАПОМНИТЬ, по-крайне мере на время изучения высшей математики в ВУЗе.

Сразу рассмотрим пример:

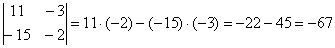
Готово. Самое главное, НЕ ЗАПУТАТЬСЯ В ЗНАКАХ.

Определитель матрицы «три на три» можно раскрыть 8 способами, 2 из них простые и 6 - нормальные.

Начнем с двух простых способов

Аналогично определителю «два на два», определитель «три на три» можно раскрыть с помощью формулы:

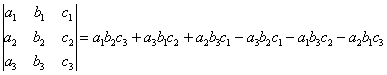
Пример:

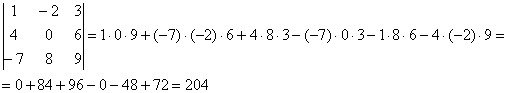
Формула длинная и допустить ошибку по невнимательности проще простого. Как избежать досадных промахов? Для этого придуман второй способ вычисления определителя, который фактически совпадает с первым. Называется он способом Саррюса или способом «параллельных полосок».
Суть состоит в том, что справа от определителя приписывают первый и второй столбец и аккуратно карандашом проводят линии:

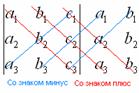
Множители, находящиеся на «красных» диагоналях входят в формулу со знаком «плюс».
Множители, находящиеся на «синих» диагоналях входят в формулу со знаком минус:

Пример:

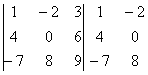
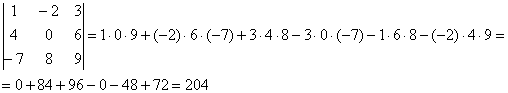
Сравните два решения. Нетрудно заметить, что это ОДНО И ТО ЖЕ, просто во втором случае немного переставлены множители формулы, и, самое главное, вероятность допустить ошибку значительно меньше.

Теперь рассмотрим шесть нормальных способов для вычисления определителя

Почему нормальных? Потому-что в подавляющем большинстве случаев определители требуется раскрывать именно так.

Как Вы заметили, у определителя «три на три» три столбца и три строки.
Решить определитель можно, раскрыв его по любой строке или по любому столбцу.
Таким образом, получается 6 способов, при этом во всех случаях используется однотипныйалгоритм.

Определитель матрицы равен сумме произведений элементов строки (столбца) на соответствующие алгебраические дополнения. Страшно? Все намного проще, будем использовать ненаучный, но понятный подход, доступный даже для человека, далекого от математики.

В следующем примере будем раскрывать определитель по первой строке.
Для этого нам понадобится матрица знаков: 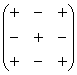. Легко заметить, что знаки расположены в шахматном порядке.

Внимание! Матрица знаков – это мое собственное изобретение. Данное понятие не научное, его не нужно использовать в чистовом оформлении заданий, оно лишь помогает Вам понять алгоритм вычисления определителя.

Сначала я приведу полное решение. Снова берем наш подопытный определитель и проводим вычисления:

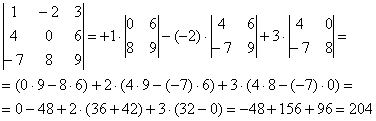
И главный вопрос: КАК из определителя «три на три» получить вот это вот:
?

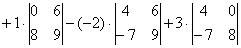Итак, определитель «три на три» сводится к решению трёх маленьких определителей, или как их еще называют, МИНОРОВ. Термин рекомендую запомнить, тем более, он запоминающийся: минор – маленький.

Коль скоро выбран способ разложения определителя по первой строке, очевидно, что всё вращается вокруг неё:

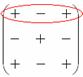
Элементы обычно рассматривают слева направо (или сверху вниз, если был бы выбран столбец)

Поехали, сначала разбираемся с первым элементом строки, то есть с единицей:

1) Из матрицы знаков выписываем соответствующий знак:

2) Затем записываем сам элемент:

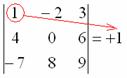
3) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит первый элемент:

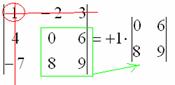
Оставшиеся четыре числа и образуют определитель «два на два», который называетсяМИНОРОМ данного элемента (единицы).

Переходим ко второму элементу строки.

4) Из матрицы знаков выписываем соответствующий знак:

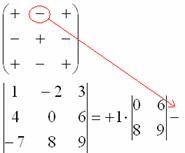
5) Затем записываем второй элемент:

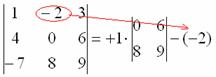
6) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит второй элемент:

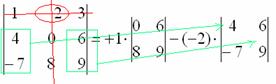
Оставшиеся четыре числа записываем в маленький определитель.

Ну и третий элемент первой строки. Никакой оригинальности:

7) Из матрицы знаков выписываем соответствующий знак:

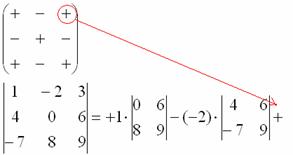
8) Записываем третий элемент:

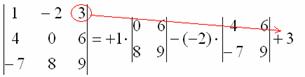
9) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит третий элемент:

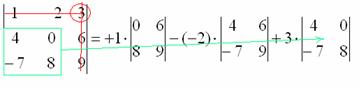
Оставшиеся четыре числа записываем в маленький определитель.

Остальные действия не представляют трудностей, поскольку определители «два на два» мы считать уже умеем. НЕ ПУТАЕМСЯ В ЗНАКАХ!

Аналогично определитель можно разложить по любой строке или по любому столбцу. Естественно, во всех шести случаях ответ получается одинаковым.

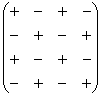
Определитель «четыре на четыре» можно вычислить, используя этот же алгоритм.
При этом матрица знаков у нас увеличится:

В следующем примере я раскрыл определитель по четвертому столбцу:

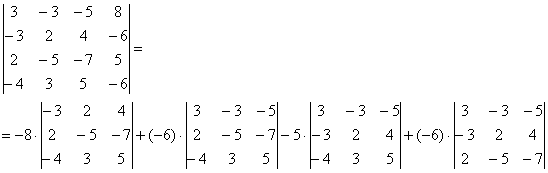
А как это получилось, попробуйте разобраться самостоятельно. Дополнительная информация будет позже. Если кто захочет прорешать определитель до конца, правильный ответ: 18. Для тренировки лучше раскрыть определитель по какому-нибудь другому столбцу или другой строке. БУДЬТЕ ВНИМАТЕЛЬНЫ!

Вычисление обратной матрицы

Продолжаем разговор о действиях с матрицами. А именно – в ходе изучения данной лекции Вы научитесь находить обратную матрицу. Научитесь. Даже, если с математикой туго.

Что такое обратная матрица? …Если интересно, посмотрите в энциклопедии, суть не в определении. А суть чаще всего в том, что вот оно, злосчастное задание, где нужно найти обратную матрицу. И это задание нужно решить либо разобраться, как оно решается.

Прежде чем приступить к рассмотрению примеров на нахождение обратной матрицы, рассмотрим один важный вопрос. Что необходимо знать и уметь для успешного изучения данного материала? Ответ. Вы должны уметь решать определители.Как вычислить определитель смотрите в соответствующей статье. Вы должны понимать, что такое матрица и уметь выполнять некоторые действия с матрицами.

Есть? Тогда поехали дальше. А хотя… ехать могут все, если Вы что-то не знаете, я буду давать нужную ссылку по ходу объяснений.

Начнем с самого ужасного и непонятного. Рассмотрим квадратную матрицу . Обратную матрицу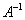 можно найти по следующей формуле:

, где 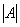– определитель матрицы , – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .

Понятие обратной матрицы существует только для квадратных матриц, матриц «два на два», «три на три» и т.д.

Обозначения: Как Вы уже, наверное, заметили, обратная матрица обозначается надстрочным индексом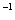

Начнем с простейшего случая – матрицы «два на два». Чаще всего, конечно, требуется найти обратную матрицу для матрицы «три на три», но, тем не менее, настоятельно рекомендую изучить более простое задание, для того чтобы усвоить общий принцип решения.

Пример:

Найти обратную матрицу для матрицы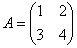

Решаем. Последовательность действий удобно разложить по пунктам.