Метод эквивалентных синусоид
При многократном повторении расчетов по характеристикам для мгновенных значений при различных значениях тока (напряжения) на нелинейном элементе можно получить ВАХ НЭ для действующих значений токов и напряжений или действующих значений их первых гармоник (предпочтительнее первое).
В результате для каждого конкретного режима можно использовать замену несинусоидально изменяющихся токов и напряжений эквивалентными им в смысле действующего значения синусоидальными величинами (эквивалентными синусоидами) и последующем применением для расчета комплексных чисел, векторных диаграмм и т.п.
Графический метод
ВАХ для действующих значений НЭ задана в виде графика.
Расчет графическим методом ведется аналогично графическому расчету нелинейных цепей постоянного тока (расчету нелинейных цепей с инерционными элементами).
Если цепь содержит активные и реактивные элементы, то токи и напряжения складываются в квадратуре (см. явление феррорезонанса).
Аналитический метод
В этом случае ВАХ аппроксимируется аналитической функцией кусочно-линейной или линейной аппроксимацией, сплайнами.
Расчет ведется аналогично цепям постоянного тока с учетом квадратуры соотношений токов и напряжений.
В тех случаях, когда вопрос о форме несинусоидальных кривых токов и напряжений не представляет особого интереса (с точки зрения эксплуатации, возможности повреждения, опасных перенапряжений и т.д.) можно воспользоваться приближенным аналитическим методом, основанным на замене действительных несинусоидальных кривых тока и напряжения эквивалентными синусоидами. Основанный на такой замене метод анализа – метод эквивалентных синусоид.
Смысл введение этого метода заключается в возможности записи уравнений в комплексной форме, а также в построении векторных диаграмм, хотя комплексные сопротивления остаются зависимыми от тока, а, следовательно, алгебраические уравнения, записанные в комплексной форме, остаются нелинейными.
Выбор эквивалентных синусоид тока и напряжения, т.е. их амплитуд и начальных фаз, может быть осуществлен тем или иным способом. Интересуясь энергетической стороной процесса, этот выбор целесообразно осуществить так, чтобы активная мощность в цепи оставалась без изменения.
В электрических проводниках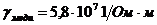 
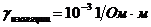
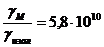
В магнитных цепях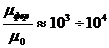 
.
Поэтому возникает поток рассеяния! Это линии с распределенными параметрами.
Пример 1.
Ток в цепи содержит:
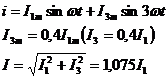
т.е. наличие 3-й гармоники, составляющей 40% от 1-й, увеличивает действующее значение несинусоидального тока по сравнению с действующим значением 1-й гармоники на 7,5%.
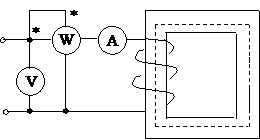
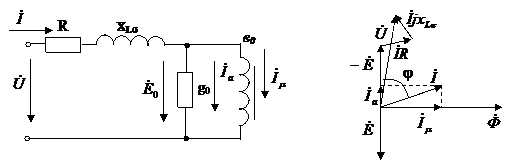
Пример 2.
u – синусоидальное
i – несинусоидальный.
Эквивалентной синусоидой должна быть первая гармоника тока, т.к.
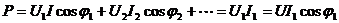
Пример 3.
u – синусоидальное
i – несинусоидальный.
Чтобы активная мощность цепи осталась неизменной p=I2r необходимо, чтобы действующее значении тока осталось неизменным, т.е. заменить несинусоидальный ток синусоидой, эквивалентной ему по действующему значению.