Векторное произведение векторов.
КООРДИНАТЫ ТОЧКИ
1. Точка на прямой.
Точка M на прямой (шкале) задается одним числом (координатой), указывающим, на сколько единиц длины точка M удалена от начальной точки O. На шкале должно быть задано положительное направление движения. Если точка M удалена в положительном направлении от O, то координата берется со знаком +, если в направлении, противоположном положительному направлению, то координата берется со знаком –. Примером является шкала температур, где температуры определяются с определенном знаком.
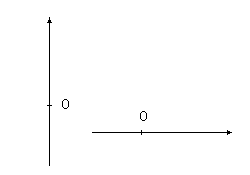
2. Точка на плоскости.
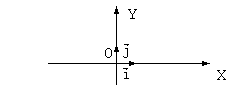
Для задания точки на плоскости приходится использовать две шкалы, называемые координатными осями (ось абсцисс и ось ординат), пересекающимися в точке O, называемой началом координат. Традиционно изображают взаимно перпендикулярные оси координат OX и OY, причем ось OX изображают горизонтально, а ось OY вертикально. Обычно принято задавать такие направления положительных движений по осям, что положительное направление оси OX после поворота на 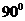 против часовой стрелки совпадает с положительным направлением оси OY. Хотя могут быть и другие варианты.
против часовой стрелки совпадает с положительным направлением оси OY. Хотя могут быть и другие варианты.
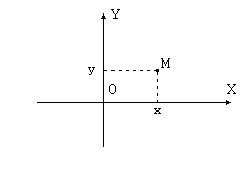
Произвольная точка M на плоскости задается координатами 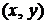 ее проекций на координатные оси. Каждая проекция получается проведением через M прямой, параллельной оси, до пересечения с другой осью. Такая система координат называется декартовой (по имени знаменитого математика и философа Рене Декарта, жившего в 17 веке).
ее проекций на координатные оси. Каждая проекция получается проведением через M прямой, параллельной оси, до пересечения с другой осью. Такая система координат называется декартовой (по имени знаменитого математика и философа Рене Декарта, жившего в 17 веке).
Другим способом задания точки на плоскости является задание точки в полярной системе координат. Для задания такой системы координат следует задать направленный луч (называемый полярной осью), который обычно изображают горизонтальным, направленным вправо. Положение точки M на плоскости задают расстоянием до начала луча (полярный радиус точки 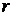 ) и углом, на который следует повернуть луч, чтобы точка оказалась на нем (полярный угол точки
) и углом, на который следует повернуть луч, чтобы точка оказалась на нем (полярный угол точки 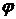 ).
).
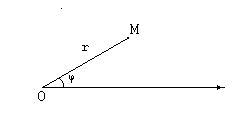
Полярные координаты точки M ( 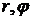 ) имеют следующие особенности: первая координата неотрицательна, а вторая координата неоднозначна, так как вместо угла
) имеют следующие особенности: первая координата неотрицательна, а вторая координата неоднозначна, так как вместо угла 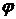 можно взять угол
можно взять угол 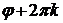 при любом целом
при любом целом 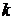 .
.
Связь между декартовыми и полярными координатами осуществляется по следующим формулам:
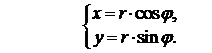
3. Точка в пространстве.
Для задания точки в пространстве требуется уже 3 координаты.
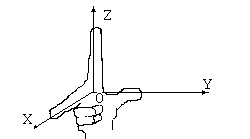
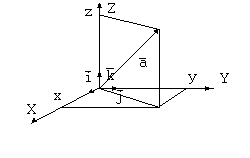
В случае декартовой системы координат мы строим 3 оси координат, традиционно взаимно перпендикулярные. Кроме того, обычно задают координатные оси OX, OY и OZ, составляющие правую тройку.Это означает, что если средний и большой пальцы правой руки, направить, соответственно, вдоль осей OX и OY в положительном направлении, то указательный палец правой руки укажет положительное направление оси OZ.
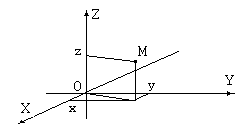
Координаты точки M 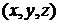 в пространстве определяется проекциями точки на соответствующие оси, причем проекции получаются проведением через M плоскостей, параллельных координатным плоскостям, до пересечения с координатными осями.
в пространстве определяется проекциями точки на соответствующие оси, причем проекции получаются проведением через M плоскостей, параллельных координатным плоскостям, до пересечения с координатными осями.
Другой координатной системой является цилиндрическая система координат. При такой системе координат задается координатная плоскость и перпендикулярная ей координатная ось. На плоскости задаются полярные координаты, причем начало полярной оси находится в точке O пересечения заданной координатной оси с заданной координатной плоскостью. Проекция точки на плоскость задается полярными координатами. Проекция точки на заданную ось определяет третью координату. Таким образом, точка M задается координатами 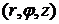 . Связь между цилиндрическими координатами и декартовыми координатами следующая: аппликата
. Связь между цилиндрическими координатами и декартовыми координатами следующая: аппликата 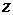 в декартовых и в цилиндрических координатах одна и та же, а координаты
в декартовых и в цилиндрических координатах одна и та же, а координаты 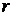 и
и 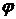 связаны с координатами
связаны с координатами 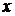 и
и 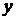 так же, как связаны декартовы и полярные координаты на плоскости.
так же, как связаны декартовы и полярные координаты на плоскости.
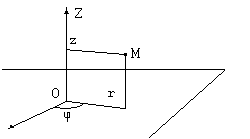
Еще одна координатная система в пространстве – сферическая система координат. Здесь также задаются плоскость и перпендикулярная ей ось. В точке их пересечения ставится точка O. Из точки O в заданной плоскости проводится полярная ось. Точка M в пространстве задается расстоянием 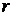 до точки O (выбор радиуса сферы), углом
до точки O (выбор радиуса сферы), углом 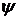 , который отрезок, соединяющий точку O с точкой M, образуют с заданной осью (выбор меридиана), а также углом, который образует проекция отрезка OM на заданную плоскость с полярной осью (выбор параллели).
, который отрезок, соединяющий точку O с точкой M, образуют с заданной осью (выбор меридиана), а также углом, который образует проекция отрезка OM на заданную плоскость с полярной осью (выбор параллели).
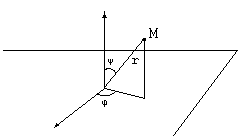
Связь между сферическими и декартовыми координатами осуществляется по формулам 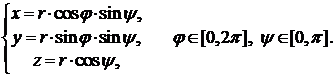
4. Расстояние между двумя точками.
Расстояние между точками проще всего измерять с помощью декартовых координат в прямоугольной системе благодаря теореме Пифагора.
Если точки 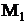 и
и 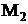 с координатами, соответственно,
с координатами, соответственно, 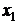 и
и 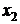 расположены на прямой, то расстояние между ними равно
расположены на прямой, то расстояние между ними равно 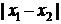 .
.
Если точки 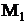 и
и 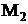 с координатами, соответственно,
с координатами, соответственно, 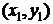 и
и 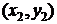 расположены на плоскости, то расстояние между ними равно
расположены на плоскости, то расстояние между ними равно 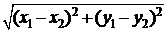 .
.
Если точки 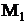 и
и 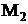 с координатами, соответственно,
с координатами, соответственно, 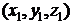 и
и 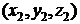 расположены в пространстве, то расстояние между ними равно
расположены в пространстве, то расстояние между ними равно 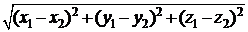 .
.
ВЕКТОРЫ
Вектор – это направленный отрезок. Он задается длиной и направлением. Иногда можно прочитать «вектор с началом в точке A и концом в точке B». Это не означает, что у вектора фиксированы начальная и конечная точка. Тот же вектор (с той же длиной и тем же направлением) можно параллельно перенести, и тогда у него будут другие начало и конец. Геометрически конец вектора традиционно обозначают стрелкой.
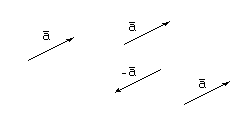
Векторы, параллельные друг другу, имеющие одинаковые длины, но противоположно направленные, называются взаимно противоположными и при записи различаются знаками.
Для того чтобы задать вектор в пространстве, проще всего поместить его начало в начало координат, тогда координаты конечной точки вектора полностью определят вектор. Поэтому векторы можно задавать с помощью координат.
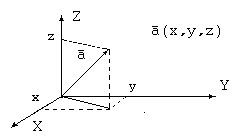
Таким образом, координаты – это проекции вектора на координатные оси. Используя координаты вектора, легко получить его длину (расстояние от конца до начала): 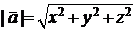 .
.
Простейшими векторами в пространстве являются векторы единичной длины, имеющие направления координатных осей. Они называются ортамии обозначаются 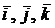 . Эти векторы имеют следующие координаты:
. Эти векторы имеют следующие координаты: 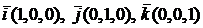 .
.
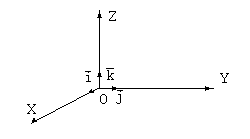
В случае вектора на плоскости XOY используются две координатные оси и каждый вектор имеет две координаты. В этом случае ортами являются векторы 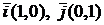 .
.
Кроме того, имеет смысл ввести нулевой вектор 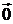 – вектор, имеющий нулевую длину и не имеющий направления.
– вектор, имеющий нулевую длину и не имеющий направления.
1. Линейные преобразования векторов.
Умножение вектора на число. Умножение вектора на положительное число 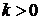 означает умножение длины вектора на это число при сохранении направления вектора. Умножение вектора на отрицательное число
означает умножение длины вектора на это число при сохранении направления вектора. Умножение вектора на отрицательное число 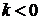 означает умножение длины вектора на число
означает умножение длины вектора на число 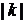 и замена направления вектора на противоположное.
и замена направления вектора на противоположное.
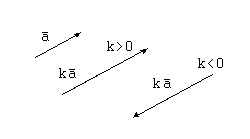
При умножении на число координаты вектора умножаются на это число: 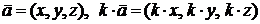 .
.
Сложение векторов. Вектор 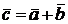 может быть получен одним из следующих способов.
может быть получен одним из следующих способов.
А) Приставим начало вектора  к концу вектора
к концу вектора  , а затем соединим начало вектора
, а затем соединим начало вектора  с концом вектора
с концом вектора  . Полученный вектор, конец которого совпадает с концом вектора
. Полученный вектор, конец которого совпадает с концом вектора  и является вектором
и является вектором 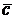 . Очевидно, что результат суммирования не зависит от перестановки слагаемых
. Очевидно, что результат суммирования не зависит от перестановки слагаемых  и
и  .
.
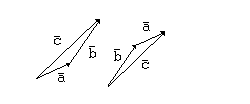
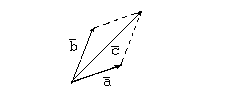
Б) Поместим начала векторов  и
и  в одну точку. Если считать эти векторы сторонами параллелограмма, то вектор
в одну точку. Если считать эти векторы сторонами параллелограмма, то вектор 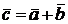 будет диагональю того же параллелограмма, причем начало вектора будут находиться в точке, совпадающей с началами векторов
будет диагональю того же параллелограмма, причем начало вектора будут находиться в точке, совпадающей с началами векторов  и
и  .
.
При сложении векторов их соответствующие координаты складываются: если вектор  имеет координаты
имеет координаты 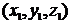 , а вектор
, а вектор  координаты
координаты 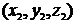 , то вектор
, то вектор 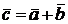 имеет координаты
имеет координаты 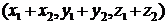 . Нетрудно показать, используя свойства подобных треугольников, что линейные преобразования векторов удовлетворяют следующему равенству:
. Нетрудно показать, используя свойства подобных треугольников, что линейные преобразования векторов удовлетворяют следующему равенству: 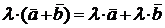 .
.
Разложение вектора по базису в трехмерном пространстве и на плоскости. Используя координаты вектора и орты, легко заметить, что вектор  с координатами
с координатами 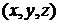 представляет собой следующую линейную комбинацию векторов-ортов:
представляет собой следующую линейную комбинацию векторов-ортов: 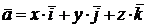 .
.
Такое представление вектора называется разложением вектора по базису, где базисом является набор ортов 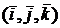 . В случае вектора на плоскости XOY базисом является набор
. В случае вектора на плоскости XOY базисом является набор 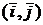 . В соответствии с количеством векторов базиса плоскость называется двумерным пространством, а пространство – трехмерным пространством.
. В соответствии с количеством векторов базиса плоскость называется двумерным пространством, а пространство – трехмерным пространством.
2. Скалярное произведение векторов.
Скалярным произведением двух векторов  и
и  является число, равное произведению длин векторов на косинус угла между ними:
является число, равное произведению длин векторов на косинус угла между ними: 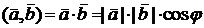 .
.
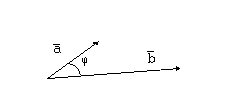
Из определения скалярного произведения следует, что 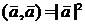 . Заметим, что в силу взаимной перпендикулярности скалярное произведение двух разных ортов равно нулю, а скалярный квадрат орта равен 1.
. Заметим, что в силу взаимной перпендикулярности скалярное произведение двух разных ортов равно нулю, а скалярный квадрат орта равен 1.
Скалярное произведение обладает свойствами: 1) 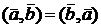 ,
,
2) 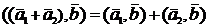 .
.
Найдем выражение скалярного произведения с помощью координат. Пусть вектор  имеет координаты
имеет координаты 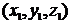 , а вектор
, а вектор  координаты
координаты 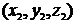 . Их разложения по базису имеют вид
. Их разложения по базису имеют вид 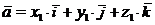 и
и 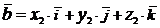 , соответственно. Используя свойства скалярного произведения, получим
, соответственно. Используя свойства скалярного произведения, получим 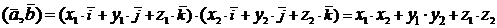 .
.
Используя скалярное произведение двух векторов, легко найти угол между этими векторами. В соответствии с определением скалярного произведения 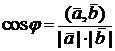 , следовательно,
, следовательно,
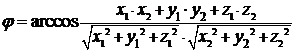 .
.
Условие взаимной перпендикулярности векторов  и
и  :
: 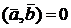 .
.
Квадратичные формы
Квадратичной формой в пространстве 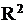 с координатами
с координатами 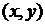 является выражение вида
является выражение вида 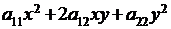 , где
, где 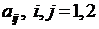 , – произвольные числа. Квадратичной формой в пространстве
, – произвольные числа. Квадратичной формой в пространстве 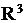 с координатами
с координатами 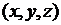 является выражение вида
является выражение вида 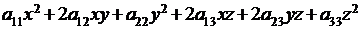 . Квадратичной формой в пространстве
. Квадратичной формой в пространстве 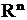 является выражение вида
является выражение вида
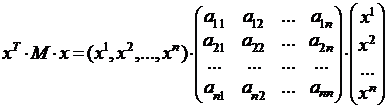 , где матрица
, где матрица 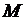 симметрична относительно главной диагонали.
симметрична относительно главной диагонали.
Часто возникает вопрос, при каких коэффициентах квадратичная форма будет сохранять знак при произвольных значениях переменных 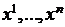 .
.
Из свойств квадратных трехчленов 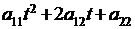 следует, что квадратичная форма
следует, что квадратичная форма 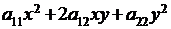 положительна тогда и только тогда, когда для коэффициентов квадратичной формы справедливы условия: 1)
положительна тогда и только тогда, когда для коэффициентов квадратичной формы справедливы условия: 1) 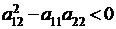 , 2)
, 2) 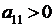 (или
(или 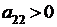 ). Она отрицательна, если
). Она отрицательна, если
1) 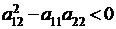 , 2)
, 2) 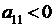 (или
(или 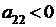 ).
).
Для квадратичной формы высших порядков рассматривают последовательность определителей 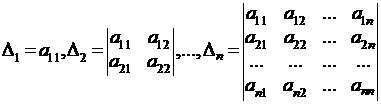 из коэффициентов матрицы
из коэффициентов матрицы 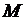 , расположенных в левом верхнем углу. Если
, расположенных в левом верхнем углу. Если 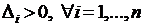 , то квадратичная форма положительна. Если
, то квадратичная форма положительна. Если 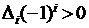 (определители с нечетными номерами отрицательны, определители с четными номерами положительны), то квадратичная форма отрицательна.
(определители с нечетными номерами отрицательны, определители с четными номерами положительны), то квадратичная форма отрицательна.
КООРДИНАТЫ ТОЧКИ
1. Точка на прямой.
Точка M на прямой (шкале) задается одним числом (координатой), указывающим, на сколько единиц длины точка M удалена от начальной точки O. На шкале должно быть задано положительное направление движения. Если точка M удалена в положительном направлении от O, то координата берется со знаком +, если в направлении, противоположном положительному направлению, то координата берется со знаком –. Примером является шкала температур, где температуры определяются с определенном знаком.

2. Точка на плоскости.
Для задания точки на плоскости приходится использовать две шкалы, называемые координатными осями (ось абсцисс и ось ординат), пересекающимися в точке O, называемой началом координат. Традиционно изображают взаимно перпендикулярные оси координат OX и OY, причем ось OX изображают горизонтально, а ось OY вертикально. Обычно принято задавать такие направления положительных движений по осям, что положительное направление оси OX после поворота на 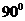 против часовой стрелки совпадает с положительным направлением оси OY. Хотя могут быть и другие варианты.
против часовой стрелки совпадает с положительным направлением оси OY. Хотя могут быть и другие варианты.
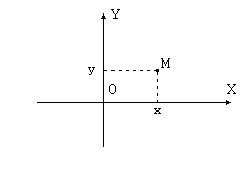
Произвольная точка M на плоскости задается координатами 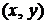 ее проекций на координатные оси. Каждая проекция получается проведением через M прямой, параллельной оси, до пересечения с другой осью. Такая система координат называется декартовой (по имени знаменитого математика и философа Рене Декарта, жившего в 17 веке).
ее проекций на координатные оси. Каждая проекция получается проведением через M прямой, параллельной оси, до пересечения с другой осью. Такая система координат называется декартовой (по имени знаменитого математика и философа Рене Декарта, жившего в 17 веке).
Другим способом задания точки на плоскости является задание точки в полярной системе координат. Для задания такой системы координат следует задать направленный луч (называемый полярной осью), который обычно изображают горизонтальным, направленным вправо. Положение точки M на плоскости задают расстоянием до начала луча (полярный радиус точки 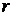 ) и углом, на который следует повернуть луч, чтобы точка оказалась на нем (полярный угол точки
) и углом, на который следует повернуть луч, чтобы точка оказалась на нем (полярный угол точки 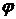 ).
).

Полярные координаты точки M ( 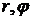 ) имеют следующие особенности: первая координата неотрицательна, а вторая координата неоднозначна, так как вместо угла
) имеют следующие особенности: первая координата неотрицательна, а вторая координата неоднозначна, так как вместо угла 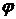 можно взять угол
можно взять угол 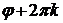 при любом целом
при любом целом 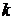 .
.
Связь между декартовыми и полярными координатами осуществляется по следующим формулам:
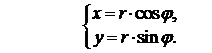
3. Точка в пространстве.
Для задания точки в пространстве требуется уже 3 координаты.
В случае декартовой системы координат мы строим 3 оси координат, традиционно взаимно перпендикулярные. Кроме того, обычно задают координатные оси OX, OY и OZ, составляющие правую тройку.Это означает, что если средний и большой пальцы правой руки, направить, соответственно, вдоль осей OX и OY в положительном направлении, то указательный палец правой руки укажет положительное направление оси OZ.

Координаты точки M 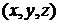 в пространстве определяется проекциями точки на соответствующие оси, причем проекции получаются проведением через M плоскостей, параллельных координатным плоскостям, до пересечения с координатными осями.
в пространстве определяется проекциями точки на соответствующие оси, причем проекции получаются проведением через M плоскостей, параллельных координатным плоскостям, до пересечения с координатными осями.

Другой координатной системой является цилиндрическая система координат. При такой системе координат задается координатная плоскость и перпендикулярная ей координатная ось. На плоскости задаются полярные координаты, причем начало полярной оси находится в точке O пересечения заданной координатной оси с заданной координатной плоскостью. Проекция точки на плоскость задается полярными координатами. Проекция точки на заданную ось определяет третью координату. Таким образом, точка M задается координатами 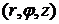 . Связь между цилиндрическими координатами и декартовыми координатами следующая: аппликата
. Связь между цилиндрическими координатами и декартовыми координатами следующая: аппликата 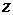 в декартовых и в цилиндрических координатах одна и та же, а координаты
в декартовых и в цилиндрических координатах одна и та же, а координаты 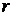 и
и 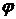 связаны с координатами
связаны с координатами 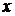 и
и 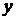 так же, как связаны декартовы и полярные координаты на плоскости.
так же, как связаны декартовы и полярные координаты на плоскости.

Еще одна координатная система в пространстве – сферическая система координат. Здесь также задаются плоскость и перпендикулярная ей ось. В точке их пересечения ставится точка O. Из точки O в заданной плоскости проводится полярная ось. Точка M в пространстве задается расстоянием 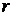 до точки O (выбор радиуса сферы), углом
до точки O (выбор радиуса сферы), углом 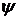 , который отрезок, соединяющий точку O с точкой M, образуют с заданной осью (выбор меридиана), а также углом, который образует проекция отрезка OM на заданную плоскость с полярной осью (выбор параллели).
, который отрезок, соединяющий точку O с точкой M, образуют с заданной осью (выбор меридиана), а также углом, который образует проекция отрезка OM на заданную плоскость с полярной осью (выбор параллели).

Связь между сферическими и декартовыми координатами осуществляется по формулам 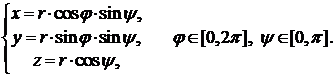
4. Расстояние между двумя точками.
Расстояние между точками проще всего измерять с помощью декартовых координат в прямоугольной системе благодаря теореме Пифагора.
Если точки 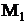 и
и 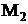 с координатами, соответственно,
с координатами, соответственно, 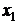 и
и 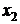 расположены на прямой, то расстояние между ними равно
расположены на прямой, то расстояние между ними равно 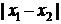 .
.
Если точки 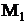 и
и 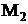 с координатами, соответственно,
с координатами, соответственно, 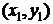 и
и 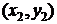 расположены на плоскости, то расстояние между ними равно
расположены на плоскости, то расстояние между ними равно 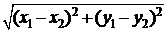 .
.
Если точки 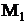 и
и 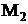 с координатами, соответственно,
с координатами, соответственно, 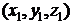 и
и 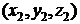 расположены в пространстве, то расстояние между ними равно
расположены в пространстве, то расстояние между ними равно 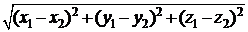 .
.
ВЕКТОРЫ
Вектор – это направленный отрезок. Он задается длиной и направлением. Иногда можно прочитать «вектор с началом в точке A и концом в точке B». Это не означает, что у вектора фиксированы начальная и конечная точка. Тот же вектор (с той же длиной и тем же направлением) можно параллельно перенести, и тогда у него будут другие начало и конец. Геометрически конец вектора традиционно обозначают стрелкой.
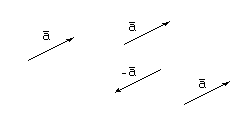
Векторы, параллельные друг другу, имеющие одинаковые длины, но противоположно направленные, называются взаимно противоположными и при записи различаются знаками.
Для того чтобы задать вектор в пространстве, проще всего поместить его начало в начало координат, тогда координаты конечной точки вектора полностью определят вектор. Поэтому векторы можно задавать с помощью координат.
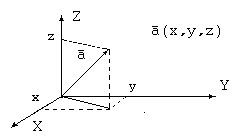
Таким образом, координаты – это проекции вектора на координатные оси. Используя координаты вектора, легко получить его длину (расстояние от конца до начала): 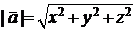 .
.
Простейшими векторами в пространстве являются векторы единичной длины, имеющие направления координатных осей. Они называются ортамии обозначаются 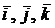 . Эти векторы имеют следующие координаты:
. Эти векторы имеют следующие координаты: 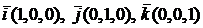 .
.
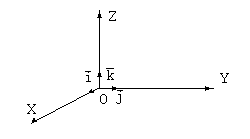
В случае вектора на плоскости XOY используются две координатные оси и каждый вектор имеет две координаты. В этом случае ортами являются векторы 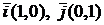 .
.

Кроме того, имеет смысл ввести нулевой вектор 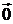 – вектор, имеющий нулевую длину и не имеющий направления.
– вектор, имеющий нулевую длину и не имеющий направления.
1. Линейные преобразования векторов.
Умножение вектора на число. Умножение вектора на положительное число 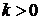 означает умножение длины вектора на это число при сохранении направления вектора. Умножение вектора на отрицательное число
означает умножение длины вектора на это число при сохранении направления вектора. Умножение вектора на отрицательное число 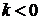 означает умножение длины вектора на число
означает умножение длины вектора на число 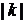 и замена направления вектора на противоположное.
и замена направления вектора на противоположное.

При умножении на число координаты вектора умножаются на это число: 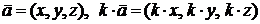 .
.
Сложение векторов. Вектор 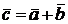 может быть получен одним из следующих способов.
может быть получен одним из следующих способов.
А) Приставим начало вектора  к концу вектора
к концу вектора  , а затем соединим начало вектора
, а затем соединим начало вектора  с концом вектора
с концом вектора  . Полученный вектор, конец которого совпадает с концом вектора
. Полученный вектор, конец которого совпадает с концом вектора  и является вектором
и является вектором 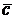 . Очевидно, что результат суммирования не зависит от перестановки слагаемых
. Очевидно, что результат суммирования не зависит от перестановки слагаемых  и
и  .
.
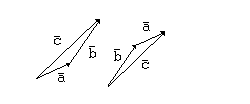
Б) Поместим начала векторов  и
и  в одну точку. Если считать эти векторы сторонами параллелограмма, то вектор
в одну точку. Если считать эти векторы сторонами параллелограмма, то вектор 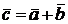 будет диагональю того же параллелограмма, причем начало вектора будут находиться в точке, совпадающей с началами векторов
будет диагональю того же параллелограмма, причем начало вектора будут находиться в точке, совпадающей с началами векторов  и
и  .
.

При сложении векторов их соответствующие координаты складываются: если вектор  имеет координаты
имеет координаты 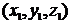 , а вектор
, а вектор  координаты
координаты 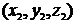 , то вектор
, то вектор 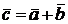 имеет координаты
имеет координаты 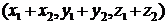 . Нетрудно показать, используя свойства подобных треугольников, что линейные преобразования векторов удовлетворяют следующему равенству:
. Нетрудно показать, используя свойства подобных треугольников, что линейные преобразования векторов удовлетворяют следующему равенству: 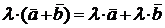 .
.
Разложение вектора по базису в трехмерном пространстве и на плоскости. Используя координаты вектора и орты, легко заметить, что вектор  с координатами
с координатами 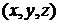 представляет собой следующую линейную комбинацию векторов-ортов:
представляет собой следующую линейную комбинацию векторов-ортов: 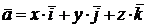 .
.

Такое представление вектора называется разложением вектора по базису, где базисом является набор ортов 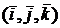 . В случае вектора на плоскости XOY базисом является набор
. В случае вектора на плоскости XOY базисом является набор 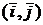 . В соответствии с количеством векторов базиса плоскость называется двумерным пространством, а пространство – трехмерным пространством.
. В соответствии с количеством векторов базиса плоскость называется двумерным пространством, а пространство – трехмерным пространством.
2. Скалярное произведение векторов.
Скалярным произведением двух векторов  и
и  является число, равное произведению длин векторов на косинус угла между ними:
является число, равное произведению длин векторов на косинус угла между ними: 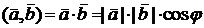 .
.
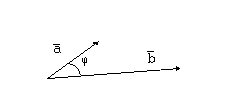
Из определения скалярного произведения следует, что 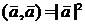 . Заметим, что в силу взаимной перпендикулярности скалярное произведение двух разных ортов равно нулю, а скалярный квадрат орта равен 1.
. Заметим, что в силу взаимной перпендикулярности скалярное произведение двух разных ортов равно нулю, а скалярный квадрат орта равен 1.
Скалярное произведение обладает свойствами: 1) 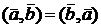 ,
,
2) 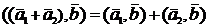 .
.
Найдем выражение скалярного произведения с помощью координат. Пусть вектор  имеет координаты
имеет координаты 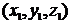 , а вектор
, а вектор  координаты
координаты 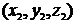 . Их разложения по базису имеют вид
. Их разложения по базису имеют вид 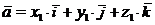 и
и 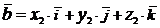 , соответственно. Используя свойства скалярного произведения, получим
, соответственно. Используя свойства скалярного произведения, получим 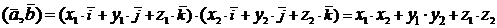 .
.
Используя скалярное произведение двух векторов, легко найти угол между этими векторами. В соответствии с определением скалярного произведения 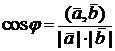 , следовательно,
, следовательно,
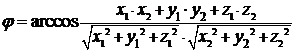 .
.
Условие взаимной перпендикулярности векторов  и
и  :
: 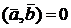 .
.
Векторное произведение векторов.
Векторным произведением двух векторов  и
и  является вектор
является вектор 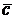 , обладающий следующими свойствами:
, обладающий следующими свойствами:
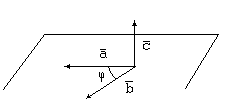
1) его длина равна произведению длин двух векторов на синус меньшего угла между ними,
2) он перпендикулярен плоскости, в которой лежат оба исходных вектора, а значит, перпендикулярен каждому из исходных векторов,
3) его направление выбрано так, что векторы  ,
,  и
и 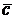 составляютправую тройку. То естьесли направить средний палец правой руки по вектору
составляютправую тройку. То естьесли направить средний палец правой руки по вектору  , а большой – по вектору
, а большой – по вектору  , то указательный примет направление вектора
, то указательный примет направление вектора 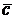 .
.
Обозначение векторного произведения: 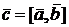 или
или 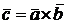 . Из определения имеем:
. Из определения имеем: 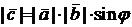 ,
, 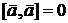 ,
, 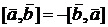 . Кроме того, справедливы свойства
. Кроме того, справедливы свойства 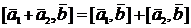 и
и 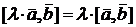 .
.
Нетрудно заметить, что 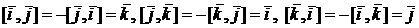 .
.
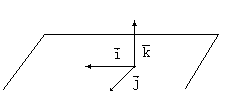
Запомнить, какой орт получается как векторное произведение двух других ортов, легко, если пользоваться следующей схемой.
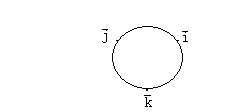
Если при движении от первого в векторном произведении вектора ко второму мы движемся против часовой стрелки, результатом векторного произведения будет третий вектор со знаком +, если по часовой стрелке, то третий вектор со знаком –.
Представляя векторы  и
и  с координатами, соответственно,
с координатами, соответственно, 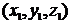 и
и 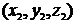 в виде разложения по базису
в виде разложения по базису 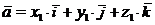 ,
, 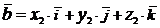 и пользуясь свойствами векторного произведения, получим:
и пользуясь свойствами векторного произведения, получим:
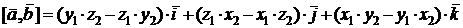 .
.
Запомнить векторное произведение в координатной форму проще всего с применением определителя:
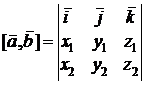 .
.
В правой части последнего равенства находится определитель третьего порядка.
Из определения векторного произведения следует, что векторное произведение двух ненулевых векторов  и
и  равно нулю тогда и только тогда, когда векторы
равно нулю тогда и только тогда, когда векторы  и
и  параллельны.
параллельны.
