Общее решение задачи о свободных колебаниях.

Общее решение строится как сумма главных колебаний с произвольными фазами, умноженных на произвольные постоянные :

,

или .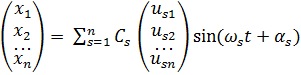

В общем решении 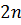произвольных постоянных 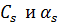, которые можем найти из 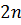начальных условий :

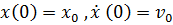Обозначим 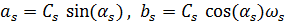и перепишем систему в виде

.

Определитель каждой из подсистем не равен нулю, поскольку его столбцы – линейно независимые формы колебаний. Постоянные 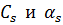выражаются через : .

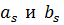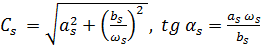Пример:

К концу вертикального стержня длиной и массой на тросе длиной 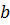подвешен груз массой . Устойчивость вертикального положения равновесия обеспечивается спиральной пружиной жесткостью .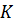

Потенциальная энергия .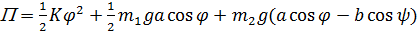

Раскладывая ее в ряд до второй степени включительно, получим

.

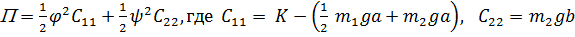Обобщенные силы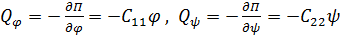

Кинетическая энергия, как уже отмечалось, записывается в момент прохождения системой положения равновесия:

, где

.

Уравнения Лагранжа

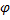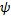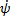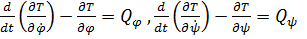
имеют вид

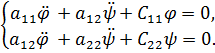(1)

Решение системы (1) будем искать в виде

,

(2)

Приравнивая определитель нулю, получим частотное уравнение

Пусть 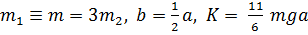.Тогда

.

Частотное уравнение примет вид

.

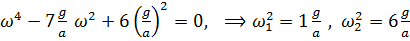Отношение амплитуд найдем из первого, например, уравнения системы (2):

. Для первой собственной частоты и главное колебание

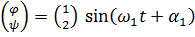, для второ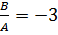й и .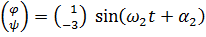

Общее решение имеет вид

.

Главные (нормальные) координаты

Независимость структуры уравнений Лагранжа от выбора обобщенных координат наводит на мысль о возможности введения таких координат, называемых главными, чтобы каждое из уравнений Лагранжа содержало бы только одну координату, или, что равносильно, чтобы матрицы жесткости и инерции были бы диагональными.

Можно было бы сослаться на теорему из линейной алгебры, которая утверждает, что две симметричные матрицы, одна из которых положительна (в данном случае это матрица инерции 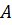), можно одним неособенным преобразованием привести к диагональному виду, но уже рассмотренные собственные формы 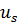позволяют без труда это сделать.

Введем новые координаты по формулам

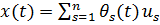или (10)

С учетом ортогональности фор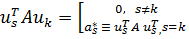м имеем

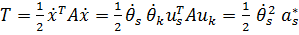
Совершенно аналогично 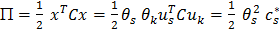, где .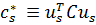

Таким образом, система уравнений Лагранжа в главных координатах распадается на 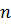уравнений вида

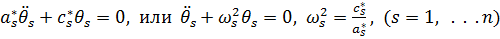, (11)

решения которых являются главными колебаниями .

Ясно, что отыскание главных координат, по сути, означает решение исходной задачи по вычислению собственных частот и форм, поэтому главные координаты имеют, главным образом, теоретическое значение, позволяющее рассмотреть некоторые особые случаи.

Случай кратных частот

В общем случае система в случае кратных собственных чисел (частот) имеет решения, содержащие время вне синуса (т.н. вековые члены). Так, в случае корня второй кратности, соответствующее решение должно иметь вид , то есть амплитуда колебаний должна неограниченно возрастать, что противоречит факту сохранения полной энергии консервативной системы.

Дело в том, что в случае симметричности матриц вековых членов не возникает, что и видно из уравнений движения в главных координатах (11).

Практически же случай равных частот весьма распространен, а иногда и желателен. Так, наиболее рациональной является такая конструкция автомобиля, при которой угловые и вертикальные колебания кузова независимы и, более того, их частоты равны.

Простой пример тела с двумя равными частотами - груз на стержне с одинаковой во всех направлениях изгибной жесткостью.

2. Случай нулевой частоты. Пример.

Если частота 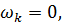то уравнение для этой координаты имеет вид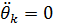

и решение 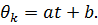Физически это решение означает, что система может совершать движение без деформации - жесткое движение.

Пример. Вал с двумя дисками[8].

Кинетическая энергия 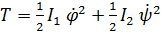, Потенциальная , где C- жесткость вала на кручение. Подставляя 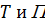в уравнения Лагранжа

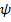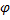получим 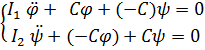(1)

Отыскивая решение в виде 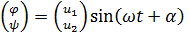, получим систему

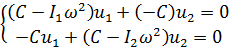. (2)

Частотное уравнение 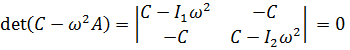имеет вид

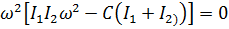, откуда .

Форму колебаний для нулевой частоты найдем формальным образом, подставляя 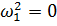в любое из уравнений системы (2), полагая амплитуду 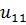равной единице: .

Эта форма «колебаний» описывает вращение дисков без деформации вала.

Форма колебаний для второй частоты .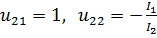

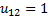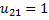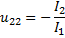Заметим, что форма, соответствующая нулевой частоте, ортогональна второй:

.

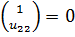Общее решение задачи удобно построить, используя главные координаты

. (3)

Подставляя (3) в выражения кинетической и потенциальной энергии, получим:

, ,

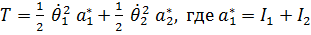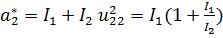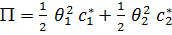, где .

Уравнения Лагранжа

.

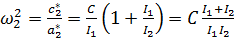Решение .