Замечание 1. Вычисление обобщенных сил для потенциальных воздействий.
Если воздействия потенциальные, т.е. 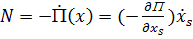 то обобщенные
то обобщенные
силы вычисляются через потенциальную энергию: 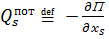
Замечание 2. Принцип возможных скоростей
Поскольку уравнения равновесия (покоя) являются частным случаем уравнений динамики и получаются из них приравниванием нулю скоростей и ускорений, т.е. левых частей уравнений ( 6.2), то в положении равновесия обобщенные силы равны нулю; отсюда в соответствии с их определением следует утверждение:
необходимым условием равновесия является равенство нулю мощности воздействий, вычисляемых на произвольных скоростях, сообщаемых телу в положении равновесия. Это утверждение называется принципом возможных скоростей (перемещений)».
Замечание 3. Обобщенные силы, обеспечивающие постулируемую зависимость координат от времени. Примеры.
Следует подчеркнуть, что изложенный выше подход позволяет вычислять обобщенные силы (воздействия) , которые обеспечивают постулируемую ранее зависимость некоторых координат от времени .
Пример 1. Математический маятник с изменяющейся длиной.
Материальная точка массы mподвешена на нити, длина которой изменяется по закону 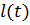 . Система имеет две обобщенные координаты -
. Система имеет две обобщенные координаты - 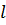 и
и 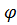 .
.
| S |
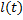 |
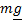 |
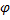 |
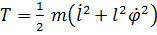 , мощность
, мощность 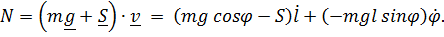
Уравнения Лагранжа 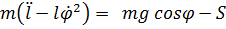 ;
;
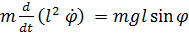
Из первого уравнения определяется натяжение нити S.
Пример 2. Движение тележки по вращающемуся стержню.
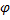 |
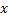 |
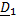 |
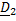 |
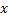 |
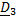 |
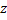 |
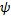 |
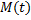 |
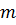 массу всех колес, которые будем считать дисками радиуса
массу всех колес, которые будем считать дисками радиуса 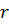 , осевой момент инерции крана
, осевой момент инерции крана 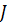 , жесткость пружины
, жесткость пружины 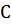 .
. Система имеет две степени свободы 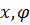 . Запишем уравнения Лагранжа
. Запишем уравнения Лагранжа
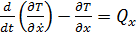 ,
, 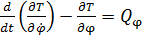 .
.
Сообщим находящейся в актуальном (т.е. произвольном) положении системе скорости 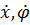 и напишем кинетическую энергию
и напишем кинетическую энергию
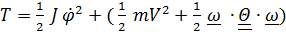 ,
,
где 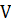 - скорость центра колеса,
- скорость центра колеса, 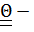 центральный тензор инерции,
центральный тензор инерции, 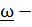 угловая
угловая
скорость колеса.
Приняв кран за подвижную систему отсчета, найдем
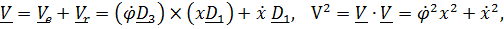
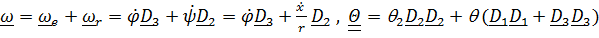 ,
,
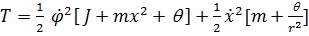 .
.
Обобщенные силы найдем «по определению» из мощности 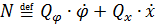 , причем ввиду независимости обобщенных скоростей можно для упрощения вычислений считать нулями все скорости кроме одной.
, причем ввиду независимости обобщенных скоростей можно для упрощения вычислений считать нулями все скорости кроме одной.
1. Положим 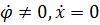 :
: 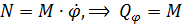 .
.
2.Положим 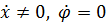 :
: 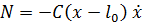 ,
, 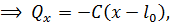
где 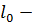 длина недеформированной пружины.
длина недеформированной пружины.
Уравнения Лагранжа будут иметь вид
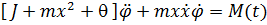
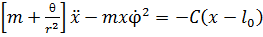
Рассмотрим частный случай движения, при котором кран вращается с постоянной угловой скоростью 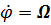 ( именно этот случай чаще всего встречается в учебных задачах).
( именно этот случай чаще всего встречается в учебных задачах).
Второе уравнение запишем в виде :
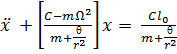 .
.
Для достаточно жесткой пружины 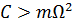 это уравнение описывает гармонические колебания
это уравнение описывает гармонические колебания
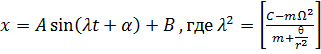 .
.
Первое уравнение дает нам значение момента, который необходим для вращения с постоянной угловой скоростью: 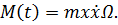
Замечание 4. О неголономных системах. Пример.
Заметим, что запись теоремы в виде ( 6.1) позволяет получать уравнения и для неголономных систем с линейными связями между скоростями вида
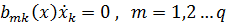 . ( 6.7)
. ( 6.7)
Для этого необходимо выразить из ( 6.7) q скоростей через (n-q) «независимых» 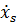 , подставить их в ( 6.1) и привести к аналогичной записи
, подставить их в ( 6.1) и привести к аналогичной записи
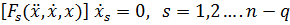 ,
,
откуда следуют уравнения 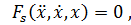
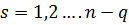 , последние совместно с уравнениями связей ( 6.7), которые, разумеется, дифференцируются, и замыкают задачу.
, последние совместно с уравнениями связей ( 6.7), которые, разумеется, дифференцируются, и замыкают задачу.
Пример 3. Движение стержня в вертикальной плоскости.
Скорость центра масс направлена вдоль стержня. Масса стержня m , момент инерции относительно горизонтальной центральной оси J.
Обобщенные координаты – декартовы координаты центра масс 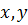 и угол поворота
и угол поворота 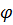 . Кинетическая энергия
. Кинетическая энергия 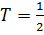 m(
m( 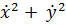 ) +
) +  J
J 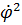 ,
,
мощность 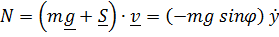 , где перпендикулярная к стержню сила
, где перпендикулярная к стержню сила 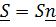 обеспечивает выполнение уравнения связи
обеспечивает выполнение уравнения связи 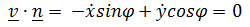
Уравнение ( 6.1) имеет вид 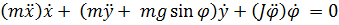 .
.
Подставляя в него уравнение связи 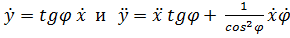 , получим
, получим
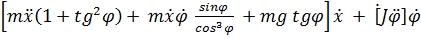 = 0,
= 0,
| mg |
| x |
| n |
 |
| y |
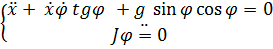
Второе уравнение сразу дает 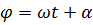 , а первое заменой
, а первое заменой 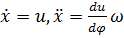 приводится к линейному уравнению
приводится к линейному уравнению 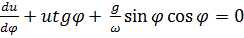 , решение которого имеет вид
, решение которого имеет вид
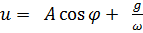
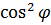 , откуда находим
, откуда находим 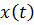 , а из уравнения связи
, а из уравнения связи 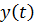 :
:
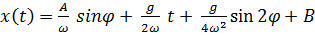 ,
,
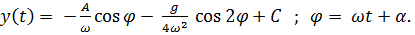
Эта задача приводится в книге 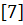 , где она решалась методом неопределенных коэффициентов Лагранжа и с помощью уравнений Аппеля.
, где она решалась методом неопределенных коэффициентов Лагранжа и с помощью уравнений Аппеля.
Пример 4. Движение точки по качающейся поверхности.
 |
 |
 |
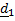 |
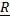 |
 |
 |
 |
По палубе раскачивающегося судна скользит материальная точка. Ориентация палубы задается углами крена j и дифферента q.Надо составить уравнения движения Лагранжа.
Ориентацию палубы проще всего описать тензором поворота 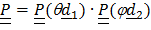 ,
,
который переводит отсчетные 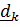 в актуальные
в актуальные 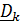 :
: 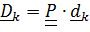 . В матричном виде
. В матричном виде
P= 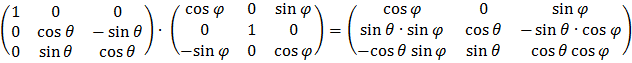
Угловая скорость 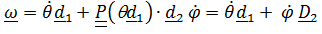 , положение точки
, положение точки 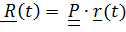 , скорость
, скорость 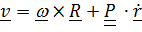 ,
, 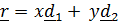 . Слагаемое
. Слагаемое 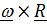 – переносная скорость,
– переносная скорость, 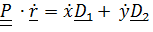 - относительная.
- относительная.
Запишем все величины в актуальном базисе 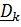 :
:
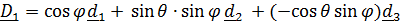
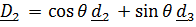
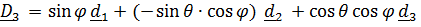
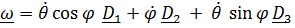
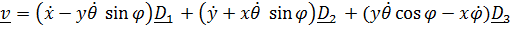
Кинетическая энергия
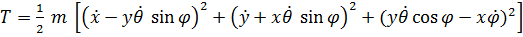 ,
,
мощность
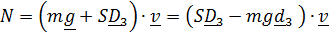 =
= 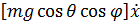 +
+ 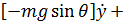
+ 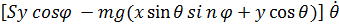 +
+ 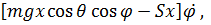
где 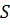 – сила, с которой палуба действует на точку, а выражения в квадратных скобках - обобщенные силы.
– сила, с которой палуба действует на точку, а выражения в квадратных скобках - обобщенные силы.
Уравнения Лагранжа для координат 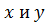 имеют вид
имеют вид
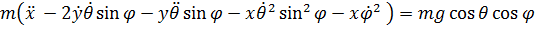 (1)
(1)
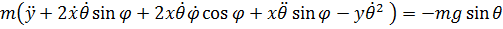 (2)
(2)
Уравнения для 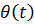 и
и 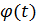 имеют вид
имеют вид
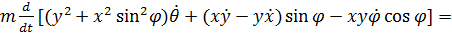
= 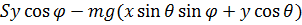 (3)
(3)
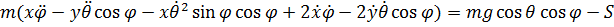 (4)
(4)
Уравнения (1) , (2) и (4)- проекции уравнения 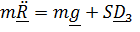 на
на 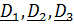 , а уравнение (3) является их следствием – это проекция закона (для точки – теоремы) об изменении кинетического момента
, а уравнение (3) является их следствием – это проекция закона (для точки – теоремы) об изменении кинетического момента 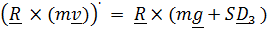 на
на 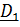 .
.
Задавая 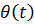 и
и 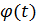 , из (1) и (2) можем найти движение точки по палубе, а из уравнений для
, из (1) и (2) можем найти движение точки по палубе, а из уравнений для 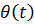 (или
(или 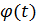 ) определим и реакцию S.
) определим и реакцию S.
Строго говоря, постулирование 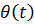 и
и 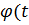 ) имеет физический смысл только при задании момента
) имеет физический смысл только при задании момента 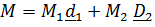 , приложенного к даже лишенной массе палубе.
, приложенного к даже лишенной массе палубе.
Приложение: Тождества типа Лагранжа для вращательных движений и их применение для получения уравнений.
Первое тождество следует из формулы Пуассона :
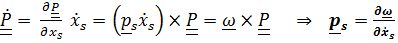
Второе получим, приравнивая смешанные производные от тензора поворота
по координате 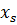 и по времени t:
и по времени t:
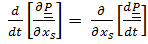 ⇒
⇒ 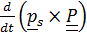
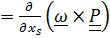 ⇒
⇒
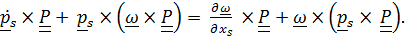
Умножим (для удобства) это равенство справа на 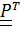 (
( 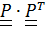 =
= 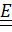 )
)
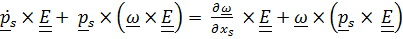
и с помощью тождеств 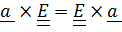 и
и 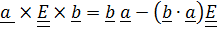
получим 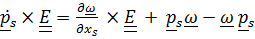 .
.
Последние два слагаемых – кососимметрический тензор, представимый в виде
( 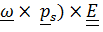 , откуда и следует второе тождество ( 6.6)
, откуда и следует второе тождество ( 6.6)
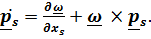
С помощью этих тождеств покажем справедливость преобразования
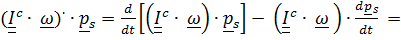
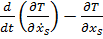 .
.
для вращательной составляющей энергии 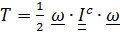 .
.
С учетом симметричности тензора инерции и первого тождества имеем
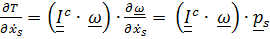 .
.
Вычислим теперь 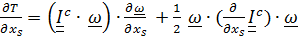 .
.
Имеем 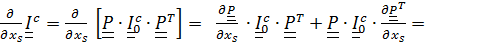
= 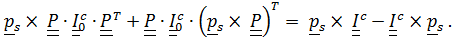
Теперь 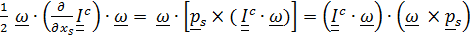
и, с учетом второго тождества

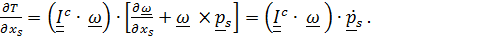
Глава 7. Колебания систем
В этом мире колеблется все – колеблются атомы и молекулы, механизмы и сооружения.
Аналитическому исследованию поддаются, как правило, только малые колебания, под которыми мы будем понимать движения, описываемые линейными дифференциальными уравнениями, даже если движение и не носит колебательного характера.
