Описание ориентации с помощью тензора поворота. Теорема Эйлера о тензоре поворота.

Рис.4.8

X

Y

Z

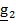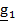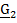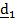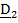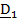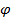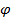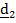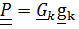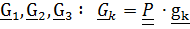Ориентация тела задается тензором поворота , переводящим жестко связанную с телом тройку векторов из отсчетного положения в актуальное (рис.4.8)

Раскладывая 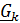по отсчетному базису, будем иметь

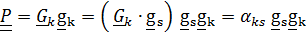, где называются направляющими косинусами.

Теорема Эйлера. Произвольная ориентация твердого тела получается из отсчетной одним поворотом на угол 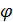вокруг оси поворота.

В математическом виде теорема сводится к следующей теореме:

Теорема о представлении тензора поворота.

Тензор поворота 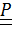, не равный 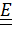, единственным образом можно представить в виде

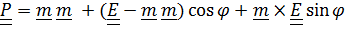, (4.18)

где 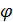-угол поворота, а единичный вектор 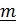задает прямую в пространстве, называемую осью поворота; положительное направление отсчета угла поворота 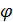согласовано с направлением 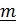в соответствии с принятой ориентацией пространства, т.е. в правоориентированном пространстве положительный поворот с конца 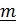виден против часовой стрелки .

Доказательство.

Покажем, что существует единственный неподвижный вектор 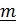, т.е. уравнение

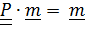имеет единственное решение. Перепишем его в виде однородного уравнения 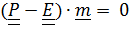, которое имеет решение, только если определитель равен нулю, что и следует из цепочки

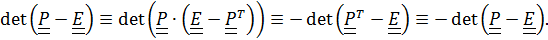
Предполагая, что существуют два решения и 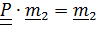, получим с помощью тождества #2 (1.13) , что означает, что и вектор 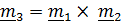также является неподвижным вектором, что невозможно ( ) .

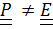Положим 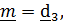а в качестве 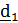и 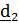возьмем любые перпендикулярные к 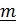и между собой единичные векторы. Поскольку тензор поворота не изменяет углов между векторами, то векторы и 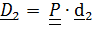лежат в плоскост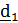и и 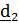(см. рис.4.8). Имеем

.

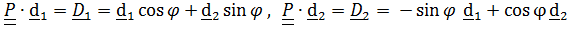Подставляя эти выражения в тензор 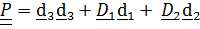и, заменяя диады, содержащие 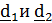на независящие от их выбора выражения

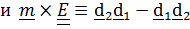, придем к (4.18): +( ) .

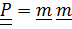Можно доказать [3] , что тензор поворота аналитически выражается через произведение , называемым вектором поворота, поэтому в дальнейшем тензор поворота будем в необходимых случаях обозначать .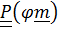

Представление (4.18) позволяет доказать весьма важную теорему:

Теорема. Если неподвижный вектор 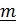тензора 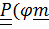), определяющий ось поворота, сам получен поворотом , то . (4.19)

Иными словами: « тензор поворота с повернутой осью равен повернутому тензору»

Доказательство. Подставляя в (4.18) , получим

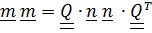, , и, полагая в тождестве #4 (1.16)

.Таким образом,

,

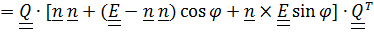или 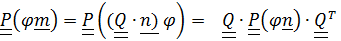ч.т.д.

Тензор спина, вектор угловой скорости, формула Пуассона.

Дифференцируя по времени уравнение , получим

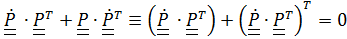или, обозначив ,

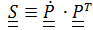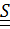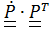, то есть тензор = , называемый тензором сп 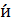на - кососимметричный, поэтому он может быть записан в виде (1.10):

, где (4.20)

называется вектором угловой скорости. Вектор 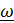задает ось вращения.

Исходя из представления Эйлера (4.18) можно прямым вычислением из (4.20) получить

(4.21)

Из (4.21) видно, что ось поворота и ось вращения совпадают только когда ось поворота неподвижна ( 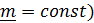, тогда .

Умножив равенство справа скалярно на 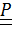, получим формулу Пуассона

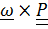. (4.22)