Оценка максимально возможного срока выполнения всего комплекса работ с определенной вероятностью

Оценки сроков выполнения всего комплекса работ с определенной вероятностью используется метод PERT (метод оценки и проверки программ), который применяется для решения проблемы неопределенности в расчетах времени выполнения работ. PERT почти полностью совпадает с методом критического пути (СР) за исключением того, что в PERT используется время работ, исходя из статистического распределения, т.е. продолжительность работы может иметь свои физические пределы (минимальное, максимальное и наиболее вероятное).

Критический путь в сетевом графике проходит через события и работы, не имеющие резервов времени, и имеет максимальную продолжительность, равную сроку свершения завершающего события. Продолжительность критического пути соответствует математическому ожиданию срока свершения завершающего события Т_ож (средняя продолжительность), равного сумме ожидаемых продолжительностей работ, составляющих критический путь.

Дисперсия срока наступления завершающего события σ²_Тож определяется в соответствии с центральной предельной теоремой теории вероятностей как сумма дисперсий работ критического пути. Зная среднюю продолжительность проекта и дисперсию можно рассчитать вероятность выполнения проекта к конкретному директивному времени Т. Вероятность свершения события к директивному сроку рассчитывается с помощью функции стандартного нормального отклонения Z. Это разница между директивным и ожидаемым временем, отнесенная к среднеквадратическому отклонению продолжительности критического пути.

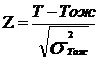
Вычислив Z, определяем вероятность р из статистических таблиц стандартного нормального распределения.

При Т = Т_ож вероятность р = 0,5. Если вероятность свершения завершающего события меньше 0,35, то опасность нарушения директивного срока велика на столько, что необходимо повторное планирование с перераспределением или дополнительным привлечением ресурсов на работы критического пути. Если вероятность больше 0,65, желательно перепланировать весь сетевой график, так как на всех его работах, включая критические, имеются избыточные ресурсы.

Можно построить сводную таблицу вероятностей свершения завершающего события к различным директивным срокам.

Пример 5.

В таблицу 6 вносят различные директивные сроки завершения проекта, ожидаемое время завершения проекта (рассчитанное в вашем проекте), среднеквадратическое отклонение. Остальные показатели в таблице рассчитываются по формуле и выбираются из статистических таблиц.

Таблица 6

Наименование показателей	Отношение директивного срока к критическому
Тож проекта
Среднеквадратическое отклонение продолжительности критического пути
Директивные сроки завершения проекта
Нормальное отклонение, Z	-0,33	0,00	0,33	0,67	1,00	1,33	1,67	2,00
Вероятность свершения проекта к директивному сроку, р	0,37	0,5	0,63	0,75	0,84	0,91	0,95	0,98

Анализ соотношения между временем и затратами на выполнение проекта

В реальных условиях выполнение отдельных или даже всех работ проектного комплекса можно ускорить путем выделения для них большего количества ресурсов (финансовых, трудовых, материальных). Это, конечно же, приводит к увеличению общих прямых затрат на выполнение работ. Вместе с тем, появляется множество различных комбинаций продолжительностей работ, при которых может быть получена некоторая требуемая плановая продолжительность проекта. Каждая комбинация может давать различные значения общей стоимости проекта.

Анализ соотношения между сроками и затратами имеет целью составление календарного плана, обеспечивающего минимальные затраты при данной продолжительности проекта.

Пример 6.

Рассмотрим в качестве примера простой проект, состоящий из 8-ми работ, исходная информация по которым представлена в таблице 7.

Таблица 7

Работа	Нормальные сроки	Сжатые сроки	Суточное прираще ние затрат, у.е.
Текущая	Предшеств.	Продолж., (время)	Затраты, у.е.	Продолж., (время)	Затраты, у.е.
A	-
B	-
C	A
D	A
E	B,C
F	B,C
G	E
H	D,F

Сетевая модель проекта показана на рис. 4.

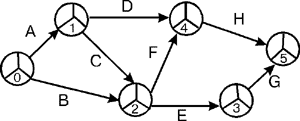
Рис. 4. Сетевая модель проекта по данным табл. 7

Каждая работа может выполняться за разное время – от верхнего «нормального» срока при некоторых «нормальных» затратах до меньшего «сокращенного» срока при соответствующих более высоких затратах. Если предполагается, что компромиссное соотношение между временем и затратами для каждой работы является линейным, то затраты при промежуточных продолжительностях работы, лежащих между нормальными и сокращенными сроками, легко определить с помощью единичного (суточного) приращения затрат для каждой работы. Например, затраты на выполнение работы В за 7 суток вместо 8 равны 400 у.е. + (8-7) х 80 у.е. = 480 у.е.

Если заданы «нормальные» продолжительности всех работ, то продолжительность проекта составит 22 суток, что видно из рис. 5.

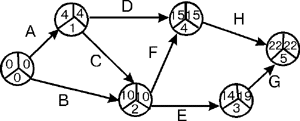
Рис. 5

Как показано на рис. 6, соответствующая стоимость выполнения всего проекта составит 3050 у.е. Заметим, что принятие неправильного решения, согласно которому ускоряется выполнение работ, не лежащих на критическом пути, не приводит к сокращению продолжительности проекта. Однако при этом стоимость проекта возрастает до величины 3870 у.е. Таким образом, «сжимать» сроки выполнения проекта можно по-разному, и задача состоит в том, чтобы сжимать с минимально возможным увеличением общей стоимости проекта.

В рассматриваемом примере общая стоимость проекта определяется суммой прямых затрат на выполнение каждой из работ.

Между верхним и нижним значениями стоимости проекта при продолжительности 22 суток возможны несколько других значений в зависимости от того, срок выполнения каких некритических работ сокращается.

Если устанавливаются сокращенные сроки выполнения всех работ, то продолжительность осуществления проекта можно сократить до 17 суток, но, как видно из рис. 6, стоимость проекта при этом возрастет до суммы в 4280 у.е. Однако, продолжительность проекта, равной 17 суток, можно достигнуть при меньших затратах без ненужного ускорения отдельных работ. Так, работа B может продолжаться не 6, а 7 суток, работа D – не 7, а 8 суток, а работа E – не 1, а 4 суток. Если все остальные работы выполняются в свои «сжатые» сроки, стоимость выполнения проекта в течение 17 суток снижается до 3570 у.е.

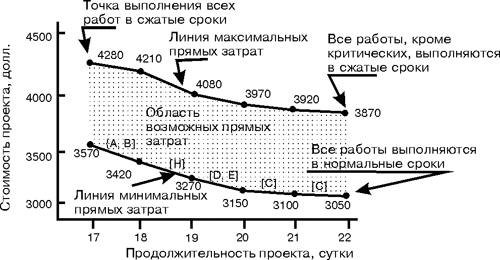
Рис. 6

Если прямые затраты определяются для каждой работы в отдельности и зависят, как правило, от объема и интенсивности использования привлекаемых для ее выполнения ресурсов, то косвенные затраты рассчитываются на проект в целом и поэтому их величина, как правило, исчисляется в пересчете на каждую единицу времени проекта (затрат/час, затрат/день и т.п.).

Минимизация общей стоимости при заданной
продолжительности проекта

Если предполагается, что продолжительность проекта не должна (или не может) меняться по каким-либо причинам, то косвенные затраты как часть общей стоимости проекта могут не учитываться при расчетах, так как они остаются постоянной величиной. Поэтому общая стоимость проекта в данном случае будет равна сумме прямых затрат, зависящих от продолжительности каждой работы в отдельности.

Продолжительность любой работы проекта можно регулировать количеством ресурсов, выделяемых для ее выполнения. В общем случае можно предположить, что эта продолжительность может изменяться между двумя границами (пессимистической оценкой) и (оптимистической оценкой). Однако, в отличие от метода PERT, в данном случае считается, что продолжительностью работ можно управлять путем выделения на их выполнение больших или меньших ресурсов. Продолжительность работы соответствует нормальному времени работы (i,j) и ее минимальной стоимости и называется нормальной продолжительностью (t_ож). Продолжительность работы соответствует такому времени выполнения работы (i,j), когда она ускорена до предела. Она называется сжатой (авральной) продолжительностью. Стоимость выполнения работы в такие сроки максимальна.

Обозначая через c_ij стоимость работы (i,j), можно допустить, что C_ij = f_ij(t_ij) в общем случае представляет из себя функцию нелинейного вида, как показано на рис. 7. Стоимость возрастает, когда убывает вплоть до границы, за которой работа уже просто не может выполняться. Представляется весьма правдоподобным, что функция продолжительности работы проходит через очень пологий минимум и затем возрастает в силу ненормальных условий работы, связанных, например, с недостатком рабочей силы или материалов. Таким образом, ее форма скорее напоминает параболу.

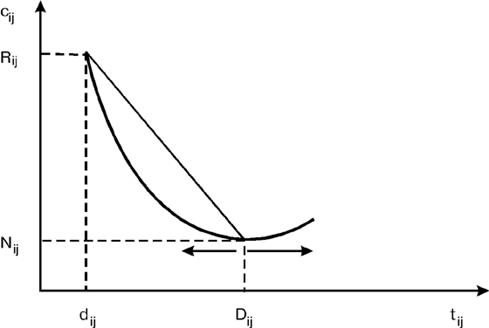
Рис. 7

В то же самое время практика показывает, что чаще всего c_ij на отрезке [d_ijD_ij] является линейной функцией от t_ij, для которой несложно найти коэффициент обратной пропорциональности s_ij продолжительности и стоимости работы, если известны стоимость нормальной продолжительности N_ij и стоимость «сжатой» продолжительности R_ij:

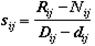
Пример 7.

Пример расчета коэффициентов пропорциональности приведен в табл. 8.

Таблица 8

Работа	Нормальные сроки	Сжатые сроки	Нормальная стоимость работ	Максимальная стоимость работ	Суточная стоимость работ
Текущая	Предшеств.	(дни)	(дни)	(у.е.)	(у.е.)	(у.е. в день)
A	-
B	-
C	A
D	A
E	B
F	D,E
G	D,E
H	G
I	G, F

Построим опорный (первоначальный) план выполнения описанного в табл. 8 проекта, взяв в качестве исходных продолжительностей работ комплекса любые значения в интервале [d_ij, D_ij], построим сетевую модель, соответствующую этим исходным данным (см. Рис. 8), и рассчитаем свободные резервы времени работ (см. Табл. 9).

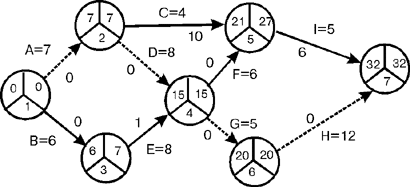
Рис. 8. Сетевая модель проекта по данным табл. 8

Таблица 9

Работа	Продолжи- тельность (дни)	Сокращение (дни)	Свободный резерв	Растяжение (дни)	Экономия общей стоимости
A
B
C
D
E
F
G
H
I

Для уменьшения общей стоимости проекта при сохранении продолжительности его выполнения в пределах продолжительности критического пути, необходимо уменьшить свободные резервы времени некритических работ с соблюдением условия d_ij D_ij. Теоретически у каждой работы есть резерв «растяжения» (D_ij - t_ij), однако не у всех работ есть свободный резерв времени, а даже у тех работ, которые имеют свободный резерв времени, он может быть значительно меньше теоретического резерва «растяжения». Поэтому, корректирующее воздействие на «растяжение» k_ij с целью уменьшения общей стоимости проекта в пределах продолжительности установленного критического пути для работы (i,j) определяется соотношением k_ij = min {(D_ij-t_ij)FF_ij}, где FF_ij – свободный резерв работы (i,j).

В рассматриваемом примере может быть увеличена продолжительность только трех работ – C, E, I, причем продолжительность выполнения работы C может быть увеличена на 6 дней, E – на 1 день и I – на 3 дня. Суммарная экономия общей стоимости проекта будет равна 1200 х 6+700 х 1+700 х 3 = 10000. До сжатия общая стоимость проекта равнялась 62200, после «растяжения» трех указанных работ она стала 52200.

В данном примере критический путь остался без изменений. Однако, в других случаях после «растяжения» могут появиться новые критические пути и работы, на которые придется обращать основное внимание.

Не следует думать, что полученный в результате проделанной процедуры «растяжения» план проекта является оптимальным по стоимости и времени. Был получен план, минимальный по стоимости при заданной продолжительности критического пути, который в общем случае может быть очень далек от оптимального.

Если задаваемая продолжительность меньше критического пути опорного плана, то сначала последовательно «сжимаются» работы на критическом пути (по принципу «чем дешевле сжатие, тем раньше оно должно быть выполнено»), а затем проделывается описанная выше процедура.