Второго порядка с постоянными коэффициентами
Уравнение вида
 , (17)
, (17)
где 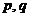 - постоянные действительные числа,
- постоянные действительные числа,  - известная непрерывная функция в интервале
- известная непрерывная функция в интервале 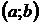 , называется линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами. Если
, называется линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами. Если 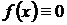 в этом интервале, то уравнение принимает вид
в этом интервале, то уравнение принимает вид
 (18)
(18)
Если уравнение (18) имеет те же коэффициенты, что и (17), то оно называется однородным уравнением, соответствующим неоднородному уравнению (17).
Для общего решения неоднородного уравнения (17) справедлива следующая теорема.
Теорема 3.1 (о структуре общего решения неоднородного уравнения)
Общее решение неоднородного уравнения (17) есть сумма общего решения соответствующего однородного уравнения (18) и любого частного решения данного неоднородного уравнения.
Общее решение однородного уравнения (18) мы находить умеем, поэтому остается рассмотреть вопрос о нахождении частного решения уравнения (17).
Для нахождения частного решения можно применять метод вариации произвольных постоянных. Однако для уравнений с постоянными коэффициентами (17) существует более простой способ нахождения частного решения, если правая часть  уравнения (17) имеет так называемый «специальный вид»:
уравнения (17) имеет так называемый «специальный вид»:
I. 
или
II. 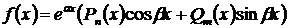
В этих случаях частное решение может быть найдено методом неопределенных коэффициентов. Суть метода состоит в следующем: по виду правой части  уравнения (17) записывают ожидаемую форму частного решения с неопределенными (неизвестными) коэффициентами, затем подставляют ее в уравнение (17) и из полученного тождества находят значения неизвестных коэффициентов.
уравнения (17) записывают ожидаемую форму частного решения с неопределенными (неизвестными) коэффициентами, затем подставляют ее в уравнение (17) и из полученного тождества находят значения неизвестных коэффициентов.
Случай I. Пусть правая часть уравнения имеет вид  , где
, где  - многочлен степени
- многочлен степени  . Тогда уравнение (17) запишется в виде
. Тогда уравнение (17) запишется в виде
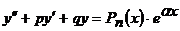 (19)
(19)
В этом случае частное решение 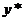 ищется в виде:
ищется в виде:
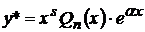 , (20)
, (20)
где 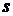 - число, равное кратности
- число, равное кратности  как корня характеристического уравнения
как корня характеристического уравнения 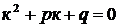 , т.е.
, т.е. 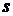 - число, показывающее, сколько
- число, показывающее, сколько
раз  является корнем характеристического уравнения;
является корнем характеристического уравнения;  - многочлен степени
- многочлен степени  , записанный с неопределенными коэффициентами
, записанный с неопределенными коэффициентами  .
.
Возможны следующие частные случаи:
а) Число  не является корнем характеристического уравнения
не является корнем характеристического уравнения 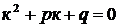 , т.е.
, т.е.  . Поэтому
. Поэтому 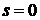 . В этом случае частное решение нужно искать в виде
. В этом случае частное решение нужно искать в виде
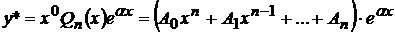
б) Число  является однократным (простым) корнем характеристического уравнения, т.е.
является однократным (простым) корнем характеристического уравнения, т.е.  или
или  ,
, 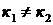 . Здесь
. Здесь  . Частное решение следует искать в виде
. Частное решение следует искать в виде
 .
.
в) Число  является двукратным корнем характеристического уравнения
является двукратным корнем характеристического уравнения 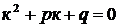 , т.е.
, т.е. 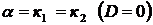 . В этом случае
. В этом случае 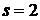 и частное решение ищем в виде
и частное решение ищем в виде
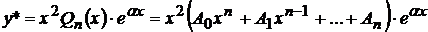
Особо отметим два частных случая уравнения (19):
1)  , т.е. правая часть уравнения (19) является многочленом степени
, т.е. правая часть уравнения (19) является многочленом степени  . В этом случае
. В этом случае 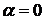 , т.к.
, т.к. 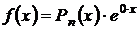 . Поэтому формула (20) имеет вид
. Поэтому формула (20) имеет вид  ,
,
где 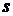 - кратность
- кратность 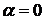 как корня характеристического уравнения
как корня характеристического уравнения 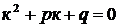 .
.
2) 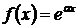 . Тогда
. Тогда  есть многочлен нулевой степени, а значит
есть многочлен нулевой степени, а значит  const.
const.
Пример 8Найти общее решение уравнения
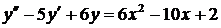 (21)
(21)
Решение: Характеристическое уравнение  имеет корни
имеет корни 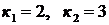 .
.
Следовательно, общее решение однородного уравнения определяется формулой 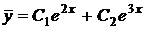 . Правая часть имеет вид
. Правая часть имеет вид 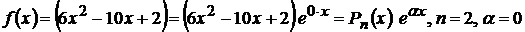 .
.
Так как 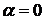 не является корнем характеристического уравнения (
не является корнем характеристического уравнения ( 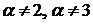 ), то
), то 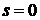 . Поэтому частное решение имеет вид
. Поэтому частное решение имеет вид 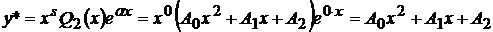 ,
,
где 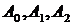 - неопределенные коэффициенты. Для удобства эти коэффициенты обозначим через
- неопределенные коэффициенты. Для удобства эти коэффициенты обозначим через  . Тогда частное решение следует искать в виде
. Тогда частное решение следует искать в виде 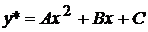 .
.
Коэффициенты  определяются методом неопределенных коэффициентов. Для этого сначала находим производные:
определяются методом неопределенных коэффициентов. Для этого сначала находим производные:
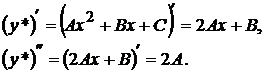
Подставив найденные выражения в исходное уравнение (21), будем иметь
 .
.
Приводя подобные члены, имеем:

Приравнивая коэффициенты при одинаковых степенях 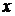 в левой и правой частях последнего тождества, получаем систему линейных уравнений:
в левой и правой частях последнего тождества, получаем систему линейных уравнений:


Решая эту систему, находим 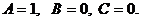
Следовательно,  .
.
Общим решением исходного уравнения (21) будет

Пример 9Найти частное решение уравнения

Решение:
Здесь  . Корнями характеристического уравнения
. Корнями характеристического уравнения  являются числа
являются числа 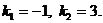 Число
Число 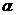 совпадает с
совпадает с 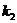 , т.е.
, т.е. 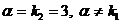 . Поэтому
. Поэтому 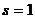 . Частное решение ищем в виде:
. Частное решение ищем в виде:
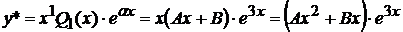 . Коэффициенты A и B определяем методом неопределенных коэффициентов. Для этого находим производные:
. Коэффициенты A и B определяем методом неопределенных коэффициентов. Для этого находим производные:

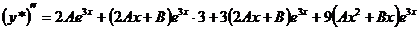
Подставляя найденные выражения в исходное уравнение (22) и сокращая обе части на  , получим тождество
, получим тождество
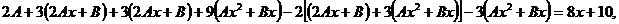
или 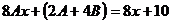 .
.
Приравнивая коэффициенты при одинаковых степенях 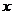 , имеем систему:
, имеем систему:
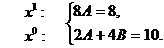
Решение этой системы есть 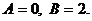
Итак, частное решение уравнения (22) имеет вид
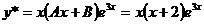 .
.
Пример 10Решить задачу Коши
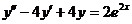 ,
, 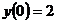 ,
, 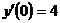 . (23)
. (23)
Решение: Характеристическое уравнение 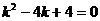 имеет один корень
имеет один корень  кратности 2 (D=0). Следовательно, общее решение однородного уравнения определяется формулой
кратности 2 (D=0). Следовательно, общее решение однородного уравнения определяется формулой  .
.
Правая часть уравнения имеет вид
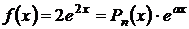 , где
, где 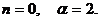
Число 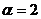 совпадает с обоими корнями характеристического уравнения, т.е.
совпадает с обоими корнями характеристического уравнения, т.е. 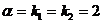 . Поэтому
. Поэтому 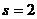 . Тогда частное решение следует искать в виде:
. Тогда частное решение следует искать в виде: 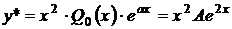 .
.
Находим производные:

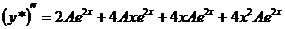 . Подставим эти выражения в исходное уравнение (23) и, сократим обе части на
. Подставим эти выражения в исходное уравнение (23) и, сократим обе части на 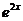 :
:
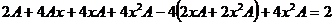 . Отсюда
. Отсюда 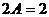 ,
, 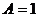 .
.
Тогда частное решение уравнения (23) имеет вид 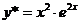 .
.
Но это частное решение не удовлетворяет начальным условиям. Поэтому находим общее решение исходного уравнения (23): 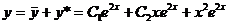 . Используя начальные условия
. Используя начальные условия 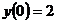 ,
, 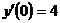 , получаем систему для вычисления значений
, получаем систему для вычисления значений 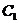 и
и 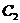 :
:

Подставив значения 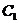 и
и 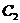 в общее решение, найдем решение задачи Коши:
в общее решение, найдем решение задачи Коши: 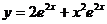 .
.
Случай II. Правая часть уравнения (17) имеет вид  , где
, где  и
и 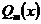 -многочлены степени
-многочлены степени 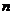 и
и 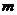 соответственно,
соответственно, 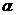 и
и 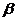 -действительные числа. Тогда уравнение (17) запишется в виде:
-действительные числа. Тогда уравнение (17) запишется в виде:
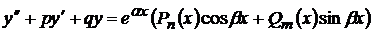 (24)
(24)
Доказывается, что в этом случае частное решение 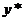 уравнения (24) следует искать в виде
уравнения (24) следует искать в виде
 , (25)
, (25)
где  - число, равное кратности
- число, равное кратности  как корня характеристического уравнения
как корня характеристического уравнения 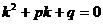 ,
,  ,
, 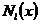 - многочлены степени
- многочлены степени  с неопределенными коэффициентами,
с неопределенными коэффициентами,  -наивысшая степень многочленов
-наивысшая степень многочленов  и
и 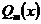 , т.е.
, т.е. 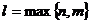 . Причем надо брать оба эти многочлена даже в том случае, когда один из многочленов
. Причем надо брать оба эти многочлена даже в том случае, когда один из многочленов  и
и 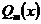 тождественно равен нулю.
тождественно равен нулю.
После подстановки функции (25) в уравнение (24) сокращают обе части уравнения на 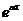 и приравнивают многочлены, стоящие перед одноименными тригонометрическими функциями в левой и правой частях уравнения. Другими словами, приравнивают коэффициенты при
и приравнивают многочлены, стоящие перед одноименными тригонометрическими функциями в левой и правой частях уравнения. Другими словами, приравнивают коэффициенты при 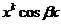 ,
, 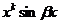 ,
,  в левой и правой частях последнего тождества и получают необходимое количество уравнений для вычисления неизвестных коэффициентов.
в левой и правой частях последнего тождества и получают необходимое количество уравнений для вычисления неизвестных коэффициентов.
Пример 11Найти общее решение уравнения
 (26)
(26)
Решение: Характеристическое уравнение  имеет корни
имеет корни 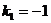 ,
, 
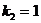 . Общее решение однородного уравнения
. Общее решение однородного уравнения  . Правая часть уравнения (26) имеет вид
. Правая часть уравнения (26) имеет вид  , т.е.
, т.е. 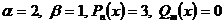 - многочлены нулевой степени. Поэтому
- многочлены нулевой степени. Поэтому 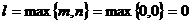 . По виду правой части уравнения составим комплексное число
. По виду правой части уравнения составим комплексное число  . Это число не является корнем характеристического уравнения, т.е.
. Это число не является корнем характеристического уравнения, т.е. 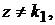
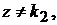 поэтому
поэтому  Следовательно, частное решение нужно искать в виде (25).
Следовательно, частное решение нужно искать в виде (25).
 , (27) где
, (27) где 
 .
.
Подставляем выражение (27) в уравнение (26). Для этого сначала находим производные: 
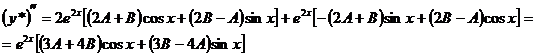
Подставляя найденные выражения в исходное уравнение (26) и сокращая обе части на 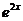 , получим тождество
, получим тождество
 .
.
Приравнивая коэффициенты при  и
и 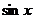 , имеем систему:
, имеем систему:

Отсюда находим 
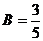 . Таким образом, частное решение имеет вид
. Таким образом, частное решение имеет вид 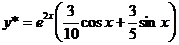 .
.
Тогда общее решение уравнения (26) определяется формулой
 .
.
Пример 12 Указать вид частного решения уравнения
 (28)
(28)
Решение: Характеристическое уравнение 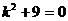 имеет корни
имеет корни  ,
, 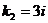 . Правая часть уравнения (28) имеет вид
. Правая часть уравнения (28) имеет вид  . Здесь
. Здесь  ,
, 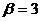 ,
, 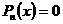 ,
, 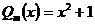 . Поэтому
. Поэтому 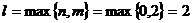 . По виду правой части составим число
. По виду правой части составим число 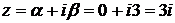 . Это число совпадает с одним корнем характеристического уравнения, т.е.
. Это число совпадает с одним корнем характеристического уравнения, т.е.  ,
,  , так что
, так что 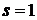 . Следовательно, искомое частное решение надо искать в виде:
. Следовательно, искомое частное решение надо искать в виде:
 .
.
Часто правая часть уравнения содержит несколько слагаемых, каждое из которых принадлежит виду I или II. В этом случае частное решение ищется в соответствии с так называемом принципом суперпозиции (наложении) решений.
Теорема 3.2 (о наложении решений). Если 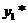 -решение уравнения
-решение уравнения 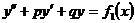 , а
, а 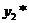 -решение уравнения
-решение уравнения 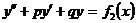 , то сумма
, то сумма  является решением уравнения
является решением уравнения  .
.
Пример 13Найти общее решении уравнения
 (29)
(29)
Решение: Характеристическое уравнение 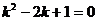 имеет корни
имеет корни 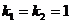 . Поэтому общее решение однородного уравнения имеет вид
. Поэтому общее решение однородного уравнения имеет вид 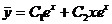 . Правая часть состоит из суммы двух функции
. Правая часть состоит из суммы двух функции 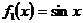 и
и  . В соответствии с теоремой 3.2 частное решение этого уравнения можно искать в виде
. В соответствии с теоремой 3.2 частное решение этого уравнения можно искать в виде  , где
, где 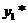 - частное решение уравнения
- частное решение уравнения
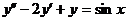 , (30)
, (30)
а 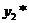 -частное решение уравнения
-частное решение уравнения
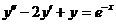 (31)
(31)
Сначала найдем частное решение 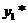 . Число
. Число  не является корнем характеристического уравнения, поэтому
не является корнем характеристического уравнения, поэтому 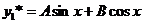 . Подставляя это выражение в уравнении (30) получаем
. Подставляя это выражение в уравнении (30) получаем 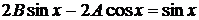 . Сравнивая коэффициенты при
. Сравнивая коэффициенты при 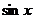 и
и  , имеем:
, имеем: 
Поэтому 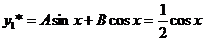 .
.
Найдем частное решение 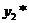 уравнения (31). Число
уравнения (31). Число 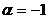 не является корнем характеристического уравнения, поэтому частное решение имеет вид
не является корнем характеристического уравнения, поэтому частное решение имеет вид 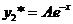 . Подставляя это выражение в уравнение (31) , находим
. Подставляя это выражение в уравнение (31) , находим  . Следовательно,
. Следовательно,  . Таким образом, частное решение данного уравнения имеет вид
. Таким образом, частное решение данного уравнения имеет вид  , а общее решение
, а общее решение  .
.
Задания для самостоятельного решения
Найти общие решения уравнений:
1) 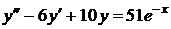 ,
,
2)  ,
,
3) 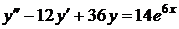 ,
,
4)  ,
,
5)  ,
,
6) 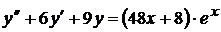 ,
,
7)  ,
,
8) 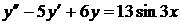 ,
,
9) 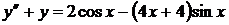 ,
,
10)  .
.
Найти решения задач Коши:
11) 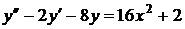 ,
, 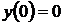 ,
,  ;
;
12) 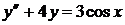 ,
, 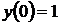 ,
,  ;
;
13)  ,
, 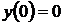 ,
, 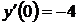 ;
;
14) 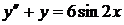 ,
,  ,
,  ;
;
15) 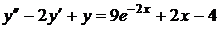 ,
, 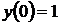 ,
, 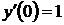
Библиографический список
1 Данко П.Е. и др. Высшая математика в упражнениях и задачах: В 2ч.-М.:Высш.шк.Ч.2.-1996.-416с.
2 Зайцев И.А. Высшая математика: Учеб.-М.: Высш.шк., 1998.-409с.
3 Пискунов Н.С. Дифференциальное и интегральное исчисления: Учебное пособие: В 2-х т.-изд. стереотип.-М.: Интегралпресс, 1997 т.1.-416с.
4 Шипачев В.С. Высшая математика: Учеб.пособие:-М.:Высш.шк., 1990.-480с.
Подписано в печать 28.06.2006 г. Формат бумаги 
Усл.печ.л. 2,44. Бумага типографская
Гарнитура «Таймс». Печать трафаретная. Заказ 518. тираж 100 экз.
4500010 г. Уфа, ул. 50 лет Октября, 34
