Второго порядка с постоянными коэффициентами
Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида
, (9)
где 
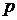и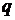 
- постоянные действительные числа.
Непосредственно можно доказать, что справедлива следующая теорема.
Теорема 2.1 Если функции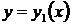 
и 
являются решениями уравнения (9), то функция 
также является решением этого уравнения при любых значениях постоянных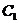 
и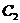 
.
Из теоремы 2.1, как следствие, вытекает, что если 
и 
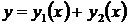- решения уравнения (9), то решениями его будут также функции 
и 
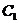. Итак, функции вида с произвольными постоянными и 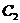являются решениями уравнения (9). Естественно возникает вопрос, не является ли выражение общим решением уравнения (9)? Для ответа на вопрос введем понятия линейной зависимости и линейной независимости функций и .
Функции и называются линейно зависимыми на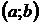 
, если существуют такие числа 
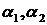, из которых хотя бы одно отлично от нуля, что для 
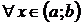имеет место равенство
(10)
Очевидно, что функции и линейно зависимы тогда и только тогда, когда они пропорциональны, т.е. 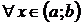выполняется равенство 
, или 
const.
Функции и называются линейно независимыми на 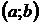, если не существуют таких чисел 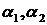, из которых хотя бы одно отлично от нуля, что для 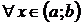имеет место равенство (10). Другими словами, равенство (10) выполняется для 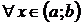тогда и только тогда, когда 
.
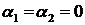Например, функции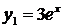 
и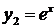 
линейно зависимы: 
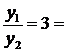const; функции 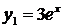и 
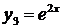- линейно независимы:
const.
Справедлива следующая теорема.
Теорема 2.2 (о структуре общего решения однородного уравнения). Если два частных решения и уравнения (9) являются линейно независимыми на 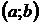, то общее решение этого уравнения имеет вид
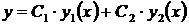, (11)
где 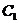и 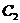- произвольные постоянные.
Из теоремы 2.2 следует, что для отыскания общего решения уравнения (9) достаточно найти два линейно независимых частных решения и составить выражения (11) с произвольными постоянным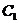и и .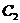
Будем искать эти частные решения уравнения (9) в виде
, (12)
где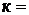 
const. Здесь 
- действительное или комплексное число, подлежащее определению. Тогда 
, 
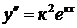. Подставляя эти выражения в уравнение (9), получим 
. Отсюда, учитывая, что 
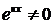, имеем:
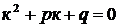(13)
Уравнение (13) называется характеристическим уравнением линейного однородного уравнения (9). Заметим, что характеристическое уравнение получается из дифференциального заменой 
на 
, 
на и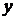 
на 1. Характеристическое уравнение (13) и дает возможность найти параметр .
Уравнение (13) является квадратным уравнением и возможны три случая.
Случай 1. Корн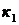и 
и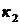 
действительные и различные: 
( 
).
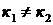В этом случае по формуле (12) получим два частных решения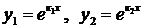 
, которые являются линейно независимыми.
Действительно,
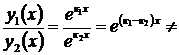const.
По теореме 2.2 следует, что общее решение уравнения (9) будет
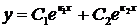(14)
Пример 5Найти частное решение уравнения 
, удовлетворяющее начальным условиям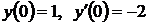 
.
Решение: Составляем характеристическое уравнение 
, откуда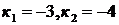 
. Поэтому общее решение есть 
. Найдем частное решение, т.е. постоянные 
и .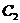
Дифференцируя общее решение, получим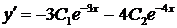 
.
Согласно заданным начальным условиям имеем:
Таким образом, искомое частное решение имеет вид
Случай 2. Корни характеристического уравнения (13) действительные и равные: 
.
В этом случае имеем лишь одно частное решение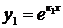 
. Вторым частным решением является функция 
(докажите самостоятельно!)
Заметим, что решения 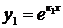и линейно независимы:
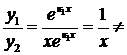const.
Следовательно, общее решение уравнения (9) имеет вид
(15)
Пример 6Найти общее решение уравнения
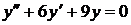
Решение: Характеристическое уравнение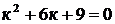 
имеет действительные и равные корни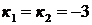 
. Поэтому согласно формуле (15) искомое общее решение имеет вид 
.
Случай 3. Корни характеристического уравнения (13) комплексные: 
Можно доказать, что следующие функции
,
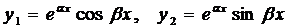являются решениями уравнения (9). Эти решения линейно независимы, так как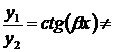 
сonst. Поэтому общее решение уравнения (9) в случае комплексных корней имеет вид
(16)
Пример 7Найти общее решение уравнения
Решение: Характеристическое уравнение имеет вид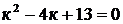 
. Находим его корни:
Отсюда 
. Поэтому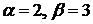 
. Согласно формуле (16) общее решение имеет вид 
.
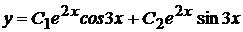Вывод: Таким образом, нахождение общего решения однородного уравнения (9) сводится к нахождению корней характеристического уравнения (13) и использованию формул (14)-(16) общего решения уравнения.
Задания для самостоятельного решения
Найти общие решения уравнений:
1) 
,
2) 
,
3) 
,
4) 
,
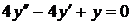5) ,
6) 
,
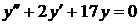7) 
,
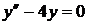8) 
,
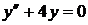9) 
,
10) 
.
Найти решения задач Коши:
11) 
, 
, 
;
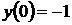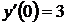12) 
, 
, 
;
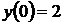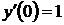13) 
, 
, ;
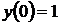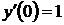14) 
, 
, 
.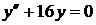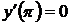