Многоканальная система обслуживания с неограниченной очередью.
Задача: В компанию приходят клиенты за консультацией о продаваемой продукции с интенсивностью 8 посещений в час. Два работника компании тратит на обслуживание каждого клиента в среднем 6 минут. Необходимо определить вероятность нахождения в приемной комнате 1, 2 и 3-х клиентов, среднее количество клиентов за час, среднее количество ожидающих консультации клиентов, среднее время ожидания.
Решение: Исходные данные для нашей задачи следующие:
λ = 8; μ =10; η = 0,8; S = 2.
 |
|
 |
|
 |
|
|
 |
|
 |
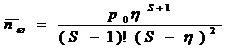Среднее время ожидания своей очереди определяется по формуле (5.13)
Подставляя исходные данные в формулы (5.9) – (5.13) получим:
1. вероятность отсутствия клиентов р0= 0,429
2. вероятность нахождения в приемной 1-го клиента р1 = 0,343
3. вероятность нахождения в приемной 2-х клиентов р2= 0,137
4. вероятность нахождения в приемной 3-х клиентов р3= 0,055
5. среднее количество клиентов, находящихся в приемной за 1 час 0,95 человека.
6. Среднее количество ожидающих обслуживания клиентов – 0,152 человека
7. Среднее время ожидания в очереди - 0,019 часа (1,14 минуты).
Многоканальная система обслуживания с ограниченной очередью
Задача: В компанию приходят клиенты за консультацией о продаваемой продукции с интенсивностью 8 посещений в час. Два работника компании тратит на обслуживание каждого клиента в среднем 6 минут. Количество мест в приемной для клиентов равно 3. Необходимо определить вероятность нахождения в приемной комнате 1, 2 и 3-х клиентов, среднее количество клиентов за час, среднее количество ожидающих консультации клиентов, среднее время ожидания.
Решение: Исходные данные для нашей задачи следующие:
λ = 8; μ = 10; η = 0,8; S = 2; К = 3; N = 5
Вероятность отсутствия в системе клиентов определяется по формуле (5.14)
 |
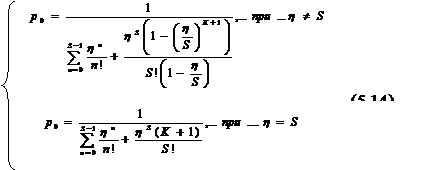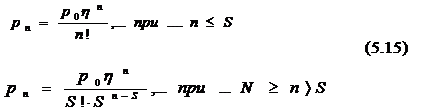Где р0 – вероятность клиентов нахождения в системе обслуживания n определяется по формуле (5.15)
 |
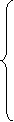Среднее количество ожидающих клиентов за час определяется по формуле (5.16)
 |
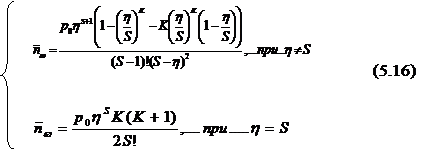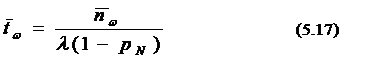Среднее время ожидания своей очереди определяется по формуле (5.17)
Подставляя исходные данные в формулы (5.14) – (5.17) получим:
1. вероятность отсутствия клиентов р0 = 0,431
2. вероятность нахождения в приемной 1-го клиента р1 = 0,345
3. вероятность нахождения в приемной 2-х клиентов р2 = 0,138
4. вероятность нахождения в приемной 3-х клиентов р3 = 0,055
6. Среднее количество ожидающих обслуживания клиентов – 0,126 человека
7. Среднее время ожидания в очереди - 0,0159 часа (0,95 минуты).
Теория игр
Задача: ЗАО «ПК Элина» продает свой товар в основном бюджетным организациям. Объём продаж зависит от финансирования организаций. Распределение объемов продаж различного вида товара от степени финансирования представлено в таблице 6.1.
Таблица 6.1 – Распределение объёмов продаж от степени финансирования
| Наименование товара | Финансирование | Прибыль, руб./шт. | Затраты на хранение, руб./шт. | |
| «Хорошее» | «Плохое» | |||
| «Южный Урал» | ||||
| «Патриот» | ||||
| «Смерч-100» | ||||
| «Смерч-200» |
Необходимо определить оптимальный объем производства каждого вида товара, обеспечивающий максимальную прибыль.
Решение: Для решения задачи воспользуемся теорией игр. Пусть игроки А и В имеют в игре между собой m и n вариантов хода. В процессе игры игрок А выбирая ход i выигрывает у игрока В сумму аij , тогда платежная матрица для игрока А будет иметь вид (6.1):
а11 а12 … а1n
а21 а22 … а2n
………………
аm1 аm2 … аmn
Математическую модель игры игрока А можно представить в следующем виде (6.2): а11 р1 + а21 р2 + …+ аm1 рm ≥ g
|
………………………………
а1n р1 + а2n р2 + …+ аmn рm ≥ g
р1 + р2 + …+ рm = 1
где рi – вероятность использования i – ой стратегии игры игроком А;
g – ожидаемый выигрыш игрока.
Для данной модели надо найти такие рi ≥ 0, удовлетворяющие уравнениям (6.2) и функция Z = g принимает максимальное значение.
Разделив все ограничения (6.2) на значение игры g и обозначив хi = рi / g для всех i, мы получим следующую систему уравнений (6.3)
а11 х1 + а21 х2 + …+ аm1 хm ≥ 1
|
………………………………
а1n х1 + а2n х2 + …+ аmn хm ≥ 1
Целевая функция примет вид: F = 1/g = х1 + х1 + …+ хm → min
(т.к. max g = min 1/g)
На основании исходных данных строим платежную матрицу (см. таблицу 6.2), где 1-я стратегия: объем производства, рассчитанный на хорошее финансирование, 2-я стратегия: объём производства, рассчитанный на плохое финансирование.
Таблица 6.2 – Платежная матрица
| «хорошее» | «плохое» | |
| 1-я стратегия | ||
| 2-я стратегия |
Элементы платежной матрицы вычисляются следующим образом:
а11 = 200 * 100 + 400 * 300 + 150 * 200 + 100 * 300 = 200000
а12 = 200 * 100 + 70 * 300 + 150 * 200 + 20 * 300 – 330 * 10 – 80 * 5 = 73300
а21 = 200 * 100 + 70 * 300 + 150 * 200 + 20 * 300 – 200 * 10 – 50 * 5 = 74750
а22 = 400 * 100 + 70 * 300 + 200 * 200 + 20 * 300 = 107000
Преобразуем платежную матрицу следующим образом:
|
|
74750 107000 1450 33700 1 23,24
Тогда система уравнений (6.3) запишется в виде:
87,38 х1 + х2 ≥ 1 х1 = 0,011
х2 ≥ 1 х2 = 0,043
Целевая функция F* = х1 + х2 = 0,011 + 0,043 = 0,054
Частота использования стратегий определяется как pi = xi * g = xi / F*, т.е. для наших данных р1 = 0,011/0,054 = 0,2
р2 = 0,043/0,054 = 0,8
Произведем противоположные действия преобразованию платежной матрицы и получим минимальную прибыль (цену игры):
υ = (1/ F* ) * 1450 + 73300 = (1/0,054) * 1450 + 73300 = 100152 руб.
Теперь определим объём производства каждого вида товара:
«Южный Урал»: 200 * 0,2 + 400 * 0,8 = 360 штук
«Патриот»: 400 * 0,2 + 70 * 0,8 = 136 штук
«Смерч-100»: 150 * 0,2 + 200 * 0,8 = 190 штук
«Смерч-200»: 100 * 0,2 + 20 * 0,8 = 36 штук.
Список использованной литературы
1. Авербах Л.И., Гельруд Я.Д. Эконмико-математические методы принятия решений: Краткий курс лекций. – Челябинск: Изд-во ЮурГУ, 2001. – 192с.