Теорема об эквивалентном генераторе

Метод эквивалентного генератора

При решении задач желательно упростить описание схемы. Один из приемов, позволяющий это сделать состоит в том, что часть схемы с двумя зажимами рассматривают как двухполюсник с описанными свойствами, не интересуясь процессами происходящими внутри него.

Двухполюсники – это любая часть схемы, рассматриваемая относительно двух зажимов.

Двухполюсники классифицируются следующим образом.

1. Пассивные двухполюсники – это такие, которые содержат только пассивные элементы и не содержат источников энергии.

2. Активные автономные двухполюсники содержат автономные источники. Если от двухполюсника отключить все внешние цепи и оставить его зажимы разомкнутыми, то обнаружится, что между ними есть напряжение (если замкнуть зажимы, то по ним потечет ток).

3. Активные неавтономные двухполюсники содержат пассивные элементы и только управляемые источники.

Метод эквивалентного генератора применяют для расчета тока в одной ветви схемы не содержащей управляемого источника и, в общем случае, не имеющей индуктивных связей с оставшейся частью схемы. Он основан на теореме об эквивалентном генераторе: любую часть схемы, рассматриваемую относительно двух зажимов, можно заменить эквивалентным генератором с параметрами 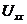, 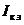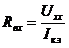_, при этом режим во внешней цепи не изменится.

МЭГ состоит в том, что сопротивление ветви, в которой требуется найти ток, считают сопротивлением нагрузки, а всю остальную часть схемы – активным двухполюсником. Этот двухполюсник заменяют эквивалентным генератором с параметрами 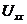, 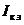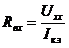_, и находят ток через сопротивление нагрузки.

Примерный порядок расчета

1. Выбирают положительное направление тока I_Н в ветви с нагрузкой.

2.Удаляют сопротивление нагрузки 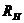и в месте разрыва изображают стрелку, направленную так же, как ток 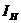в ветви нагрузки. Стрелка указывает направление напряжения холостого хода .

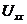3. Находят величину :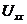

- записывают уравнение по второму закону Кирхгофа для фиктивного контура, включающего 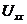и не вносящего дополнительных неизвестных U_J;

- в режиме холостого хода рациональным методом находят токи ветвей, входящие в уравнение для ;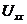

- рассчитывают величину .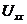

4. Определяют входное сопротивление R_BX относительно точек разрыва. Возможно несколько способов:

а) ,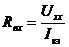

где 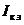- ток короткого замыкания, направленный также как ;

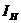б) при отсутствии в схеме управляемых источников расчет входного сопротивления рациональнее всего выполнять сворачиванием схемы к входным зажимам пассивной схемы, полученной из активной схемы, путем замены автономных источников энергии их внутренними сопротивлениями;

в) в схеме с автономными и управляемым источниками энергии автономные источники энергии заменяют их внутренними сопротивлениями. К зажимам полученной схемы подключают пробный источник и рассчитывают неизвестный пробный ток. Получают 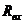как

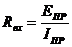
при одинаковом направлении .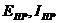

5. Рассчитывают ток через сопротивление нагрузки

.

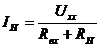Пример: Дано: , , , , , , .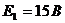

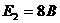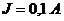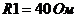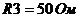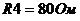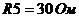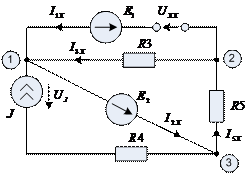
Рис. 2.6.1

=>

,

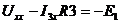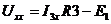
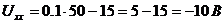где 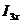- ток 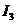в режиме холостого хода. 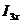можно найти:

1) из системы уравнений по законам Кирхгофа

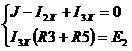
Откуда .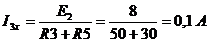

2) по методу наложения

, ,

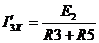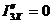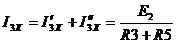
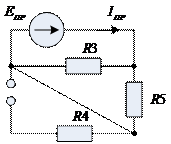
рис. 2.6.2

Согласно рис. 2.6.2:

.

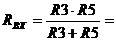
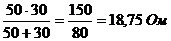Тогда: 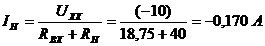.