Электрическая схема и её элементы
Электрический ток проходит по некоторым устройствам, совокупность которых называют электрической цепью (резисторы, катушки, конденсаторы, лампы, двигатели). В теории цепей рассматривают не саму цепь, а упрощенную модель, в которой сохраняют основные свойства цепи. Условное изображение этой модели называют электрической схемой или просто схемой. Схему составляют из типовых (стандартных) элементов, каждый из которых имеет строго описанное главное (одно) свойство реального устройства. Если реальное устройство обладает несколькими свойствами, которые необходимо учесть, то в схеме изображают несколько типовых элементов.
Типовые элементы
1. Провод
На схемах провода не имеют сопротивления Rпр=0. Поэтому при любой их длине и любом токе все точки провода имеют один и тот же потенциал (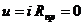 
). Длину провода и его конфигурация определяют из удобства изображения схемы.
2. Сопротивление R [Ом]
Главное свойство R - потребляет мощность.
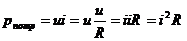[Вт].
Обратную величину называют проводимостью: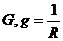 
[См].
3. Индуктивность L [Гн]
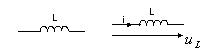
Главное свойство L - запасать энергию в магнитном пол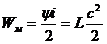е 
, где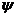 
- потокосцепление - сумма магнитных потоков, пронизывающих витки катушки. Индуктивность L – коэффициент пропорциональности 
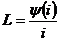[Гн],между потокосцеплением 
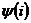магнитного потока, созданного током, проходящим через рассматриваемую катушку, с витками этой же катушки. По закону Ленца при L=const 
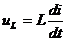. Таким образом, 
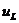зависит не от величины тока, а от скорости его изменения. При постоянном токе 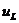=0 и индуктивность заменяется проводом.
4. Емкость С [Ф]
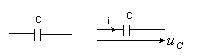
Главное свойство С - запасать энергию в электрическом поле.
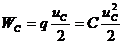, емкость 
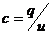- коэффициент пропорциональности между зарядами и напряжением между обкладками конденсатора. Тогда 
.
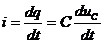Ток через емкость зависит не от напряжения, а от скорости изменения приложенного напряжения.
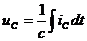. При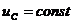 
ток через емкость не течет, и емкость заменяется разрывом.
Все рассмотренные выше элементы называют пассивными. Они не могут генерировать электрическую энергию. Есть и активные элементы, которые при определенных условиях могут генерировать электрическую энергию. Таких элементов два: идеальный источник напряжения (ЭДС) и идеальный источник тока.
1. Источник напряжения (ЭДС) e, E - это такой элемент, напряжение между зажимами которого при любом токе, по величине равно ЭДС.
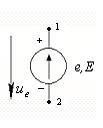
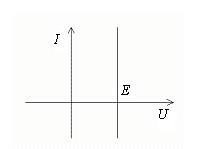
Стрелка внутри источника показывает направление возрастания потенциала внутри источника. Если е=0, то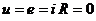 
на этом участке при любом токе. Это значит, что е=0 заменяется проводом Rпр = 0 и поэтому считают, что внутреннее сопротивление источника напряжения Rвн е = 0.
2. Источник тока j, J– это такой элемент, через который при любом напряжении между его зажимами проходит один и тот же ток равный величине источника тока. Если величина источника тока равна 0 (j=0), то i = j = u/R = 0, то при любом напряжении ток на этом участке будет равен нулю (разрыв цепи). Поэтому считают, что внутреннее сопротивление источника тока бесконечно: Rвн j =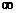 
.
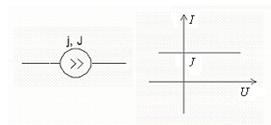
Источники тока обеспечивают смещения транзисторов; незаменимы в качестве активной нагрузки для усилительных каскадов с большим коэффициентом усиления и в качестве источников питания эмиттеров для дифференциальных усилителей; необходимы для работы таких устройств как генераторы пилообразного напряжения, интеграторы. Они необходимы для построения схем замещения транзисторов, ламп, любых активных устройств.
Рассмотренные источники ЭДС и тока называются автономными (неуправляемыми, независимыми). Существуют управляемые (зависимые) источники ЭДС и тока.
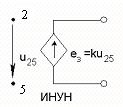
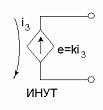
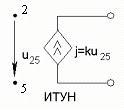
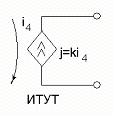
Рис.1.2.1
На рис.1.2.1 использованы следующие сокращения:
ИНУН – источник напряжения управляемый напряжением;
ИНУТ – источник напряжения управляемый током;
ИТУН – источник тока управляемый напряжением;
ИТУТ – источник тока управляемый током.
Используя стандартные элементы, можно строить схемы замещения реальных элементов цепи.
1.3 Топологические элементы схем
Кроме рассмотренных элементов существуют топологические элементы, которые позволяют описать структуру цепи.
Основные понятия:
1) Ветвь – соответствует участку цепи, в котором все элементы стоят последовательно, т.е. по которому протекает один и тот же ток.
2) Узел – место соединения трех и более ветвей (иногда даже двух ветвей – фиктивный узел).
3) Граф – условное изображение схемы, дающее положение всех узлов и ветвей без указания элементов. Графы делят на связные и несвязные.
связный граф несвязный граф
Связный – из любого узла можно попасть в любой другой по ветвям.
4) Любая часть графа называется подграфом.
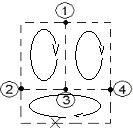
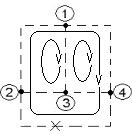
5) Контур – замкнутый путь по ветвям.
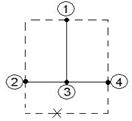
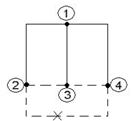
6) Дерево – связный подграф, содержащий все узлы, но не образующий ни одного контура. Примеры деревьев:
7) Ветви, не вошедшие в дерево, называются ветвями связи.
8) Главный контур – это контур, полученный из ветвей дерева и только одной ветви связи.
Пример:
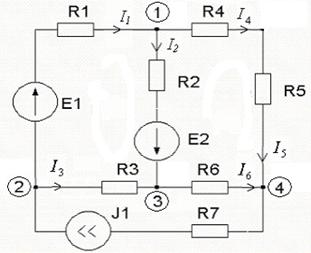
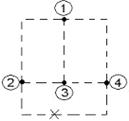
1.4 Основные законы цепей
1. Первый закон Кирхгофа
Алгебраическая сумма мгновенных значений токов ветвей, сходящихся в одном узле, равна нулю: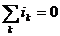 
.
Токи, входящие в узел, берутся с одним знаком, а выходящие – с противоположным.
2. Второй закон Кирхгофа
Алгебраическая сумма мгновенных значений напряжений на всех элементах контура равна нулю: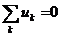 
.
Выбирают направление обхода контура и тогда напряжения, совпадающие с направлением обхода контура, берут со знаком плюс, а направленные навстречу – со знаком минус. Так как напряжение на источнике ЭДС в точности равно самой ЭДС, а направлено в обратную сторону, удобно применять другую формулировку второго закона Кирхгофа: Алгебраическая сумма мгновенных значений напряжений на всех элементах контура, кроме источников ЭДС, равна алгебраической сумме мгновенных значений ЭДС этого же контура.
.
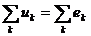Для напряжений правило знаков тоже, что и в первой формулировке, а ЭДС берут со знаком плюс, если направлено так же, как и обход контура.
3. В любой отдельно взятой цепи выполняется баланс мощностей
Сумма мощностей генерируемых равна сумме мощностей потребляемых:
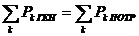или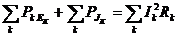 
Пример:
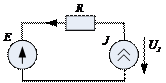
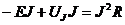, где 
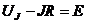и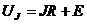 
.