Законы распределения случайной величины
Законы распределения случайной величины - это соотношения, устанавливающие связь между возможными значениями случайных величин и соответствующими значениями вероятностей или частот (частостей). Закон распределения случайной величины позволяет определить вероятность (частоту, частость) появления случайной величины в любом интервале ее возможных значений.
Дискретные случайные величины Х могут принимать только ряд отдельных значений х1,х2,...,хn; каждому значению соответствует определенное значение вероятностей Р1,Р2,...,Рn. Эти события образуют полную группу несовместных случайных событий, для которых
Р1+Р2+...+Рn=  =1.
=1.
Распределение прерывной случайной величины может быть представлено в виде таблицы (табл. 1), называемой рядом распределения, или графически (рис. 2) - многоугольника распределения.
(ЭНО), то есть модель испытания объектов на долговечность, применяют для определения вероятностных характеристик ресурса и срока службы объектов, а также наработки до первого отказа.
Статистическую информацию об отказах получаем при наблюдениях за эксплуатацией или испытаниями при определенных условиях N одинаковых объектов. При этом каждый объект работает от начала эксплуатации до первого отказа, не восстанавливается и не заменяется новым (работоспособным). Испытания заканчивают после отказа всех объектов. Наработка каждого объекта до первого отказа записывается в виде вариационного ряда
t1<t2<...<ti<...<tN.
Закон распределения случайной величины является ее универсальной вероятностной характеристикой.
В модели ЭНО случайным событием является отказ объекта, а случайной величиной - ресурс, то есть наработка объекта от начала эксплуатации до перехода в предельное состояние. Случайные события будут полностью описаны с вероятностной точки зрения, если задать распределение вероятностей соответствующих им случайных величин.
Законом распределения вероятностей называют соотношения, устанавливающие связь между возможными значениями случайной величины и соответствующими им вероятностями. Этот закон имеет разные формы:
1) ряд распределения;
2) интегральная функция распределения;
3) дифференциальная функция распределения.
Интегральная функция распределения вероятностей
Случайной величины
Интегральная функция распределения вероятностей случайной величины - одна из форм закона распределения.
Наибольшее распространение в теории надежности имеют события вида Х<х, то есть случайная величина Х принимает значение, меньшее некоторого действительного числа х. Рассматривая действительное число х как независимую переменную, получают интегральную функцию распределения случайной величины Х.
Интегральной функцией распределения случайной величины Х называется функция F(x), определяющая вероятность события Х<х для каждого значения аргумента х, то есть
F(x)=P(Х<х).
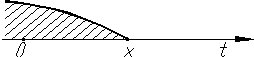 |
Геометрически это значит, что F(x) - вероятность того, что случайная величина х примет значение, изображенное на числовой оси точкой, расположенной левее точки х (рис. 7).
Рис. 7. Геометрический смысл интегральной функции распределения
Интегральная функция F(x), как всякая вероятность, - величина безразмерная. Она полностью характеризует случайную величину (с вероятностной точки зрения) и является самой универсальной характеристикой случайной величины, т.к. существует и для дискретных, и для непрерывных случайных величин. Для краткости используют следующие термины:
1) интегральная функция распределения;
2) интегральная функция;
3) функция распределения.
