Математические методы теории надежности

Механическое оборудование в результате эксплуатации в различных условиях подвергается не только переменным, но и случайным воздействиям. Поэтому для анализа и контроля надежности используется теория вероятностей и математическая статистика.

Оценка надежности объектов при помощи математических методов на основе обобщения накопленной статистической информации об их работе в реальных условиях эксплуатации позволяет выявлять вероятностные закономерности и соотношения между случайными факторами. Они в различной мере влияют на работоспособность, безотказность, долговечность объектов.

2.1. Основные понятия и определения

В теории вероятностей и основанной на ней математической статистике применяют следующие специфические понятия:

1) испытание (опыт);

2) событие;

3) случайная величина;

4) частота;

5) частость;

6) вероятность.

Испытание (опыт) - это практическое создание определенной совокупности условий, влияющих на некоторое физическое явление. Испытание сопровождается регистрацией результата.

Событие - это явление, происходящее в результате испытания (опыта). Оно является качественным результатом испытания. Например, результатом испытания механического оборудования в определенных условиях с целью оценки его надежности. Различают следующие события: достоверные, невозможные, случайные, единичные, массовые, несовместные.

Достоверное - событие, которое неизбежно произойдет при данных действующих условиях.

Невозможное - событие, которое при тех же условиях произойти не может.

Случайное - событие, которое при рассматриваемом сочетании условий может произойти, а может и не произойти, (например, появление отказов).

События в технике подразделяют также на единичные и массовые. Единичное - событие, которое возникло однократно и при многократном воспроизведении того же испытания (опыта) практически не повторится. Массовые - события, которые повторяются.

Несовместные - события, происходящие в том случае, если при испытании появление одного из них исключает возможность появления другого (например, отказ и работоспособность).

Случайная величина - это величина, которая может принять какое-либо неизвестное заранее возможное значение, зависящее от случайных факторов (причин), которые не могут быть учтены. Случайные величины могут быть дискретными и непрерывными.

Дискретной (прерывной) случайной величиной называется случайная величина, принимающая отделенные друг от друга возможные значения, которые можно записать в виде последовательности

t₁, t₂, ... , t_n, ... .

Число возможных значений дискретной случайной величины может быть конечным и бесконечным.

В теории надежности дискретными случайными величинами являются:

1) количество невосстанавливаемых объектов, отказавших в заданном интервале времени;

2) количество отказов восстанавливаемого объекта в заданном интервале времени;

3) количество объектов, восстановленных в заданном интервале времени.

Непрерывной случайной величиной называется случайная величина, возможные значения которой непрерывно заполняют некоторый конечный или бесконечный промежуток. Число возможных значений непрерывной случайной величины, очевидно, бесконечно.

В теории надежности непрерывными случайными величинами являются:

1) наработка;

2) ресурс;

3) срок службы;

4) время восстановления;

5) срок сохраняемости.

В теории вероятностей изучаются массовые случайные отказы или величины, имеющие к тому же устойчивую частоту появления.

Частота - число одинаковых или близких (полученных по наблюдениям) появлений событий или абсолютных значений случайных величин, соединенных в одну группу (интервал) или разряд.

Частость (относительная частота) - частота, выраженная в долях единицы или процента от общего числа испытаний или объектов изучаемой совокупности. Например, если проведено N испытаний машин и получена частота (количество) отказов m, то относительная частота (частость) отказов

Q= 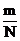или Q= 100 (%). (1)

При неограниченном увеличении N статистическое значение Q приближается или сходится к некоторому числу P, называемому вероятностью данного события:

P = lim Q = lim 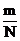, то есть P(A) ,

где P(A) - вероятность события А; m - число случаев, благоприятствующих наступлению события А; N - число несовместных единственно возможных и равновозможных событий.

При многократной реализации одной и той же совокупности условий обнаруживаются закономерности в наступлении случайных событий. Это и есть одна из задач теории вероятностей.

Изучение закономерностей появления отказов как случайных событий является центральным вопросом всей проблемы надежности.

Для количественной оценки случайного события используют вероятность того, что случайная величина окажется в указанном интервале ее возможных значений. Вероятность - объективная математическая оценка возможности реализации случайного события или случайной величины.

Теоремы теории вероятностей

1. Формула сложения вероятностей. Если при испытаниях может произойти только одно из рассматриваемых событий A₁, A₂,...,A_n, а вместе они появиться не могут, то эти события несовместные. Рассматриваемое сложное событие А называют суммой исходных событий:

A=A₁+A₂+...+A_n= 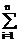A_i.

Если вероятности событий подчиняются таким же соотношениям, как и соответствующие им частости, то получим теорему (формулу) сложения вероятностей:

P(A)=P(A₁+A₂+...+A_n)=P(A₁)+P(A₂)+...+P(A_n)= 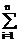P(A_i).

B общем случае для полной группы несовместных событий

P(A_n)= 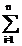P(A_i)=1. (2)

Полная группа событий - события, когда в результате испытаний обязательно наступит хотя бы одно из них. Например, при длительных испытаниях механического оборудования обязательно появится отказ.

Для двух несовместных событий A и 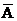, образовавших полную группу,

P(A)=1-P( 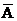). (3)

Например, в надежности чаще рассматриваются два несовместных противоположных события - состояние работоспособности и отказ. Они составляют полную группу.

Для двух совместных событий A₁ и A₂, образовавших полную группу,

P(A₁+A₂)=P(A₁)+P(A₂)-P(A₁A₂). (4)

2. Формула умножения вероятностей. Если события независимы, то появление одного из них не изменяет вероятности появления другого:

P(AB)=P(A)P(B). (5)

Для двух зависимых событий

P(A)=P(B)P(AB)=P(A)². (6)

Сложное событие A, заключающееся в одновременном осуществлении нескольких событий, называется произведением исходных событий A_i:

A=A₁A₂...A_n= .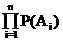

Вероятность независимых событий по теореме умножения вероятностей

P(A)=P(A₁,A₂,...,A_n)=P(A₁)P(A₂)...P(A_n)= 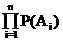. (7)

Если

P(A₁)P(A₂)=...=P(A)=P,

то

= .
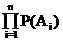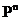