Статистика. Вопрос 2. Теоремы сложения и умножения вероятностей. Условные вероятности.

Статистика.

1.

Случайное событие – событие, которое в ходе испытании может произойти, а может и не произойти

Классическое определение вероятности:

Вероятностью Р(А) случайного события А называется отношение кол-ва m элементарных событий А к общему кол-ву элементарных событий n.

Р(А)=m/n

Статистическое определение вероятности:

Вероятность – это число Рст(А), около которого группируются значения относительной частоты р*(А) наступления случ.события А при неограниченном возрастании кол-ва испытаний

Совместные события (А1,А2,А3…). Осуществление любого из них в рез-те испытания не исключает осуществления при этом любого другого из перечисленных событий.

Несовместные события (А1,А2,А3…). Осуществление любого из событий в рез-те испытания исключает осуществление при этом других перечисленных событий.

Зависимое событие. На его вероятность оказывает влияние исход какого-либо иного события.

Независимое событие. Б независимо от А, если появление или не появление события А не влияет на вероятность события Б.

Статистика. Вопрос 2. Теоремы сложения и умножения вероятностей. Условные вероятности.

Теорема сложения: вероятность появления какого-либо события из нескольких несовместных равна сумме их вероятностей. P(A или B)=P(A)+P(B)

Теорема умножения: вероятность совместного появления независимых событий равна произведению их вероятностей. P(A и B)=P(A)*P(B)

Условная вероятность – вероятность некоторого события при условии того, что другое событие произошло, либо не произошло. Например, событие А произойдет при условии реализации события В. В таком случае используют обозначение Р(А/В).

Теорема умножения вероятностей для зависимых событий: вероятность наступления случайного события А и зависящего от него события В равна произведению вероятности события А на условную вероятность события В. P(A и B)=P(A)*P(B/А)

Статистика. Вопрос 6. Непрерывные и дискретные случайные величины. Закон распределения Пуассона. Формулы для математического ожидания и дисперсии. Примеры.

Непрерывные величины принимают бесконечное число возможных значений в конечном, или в бесконечном интервалах изменения. Например, время, масса, объем.

Дискретные величины могут принимать конечное, счетное число случайных значений. Например, год рождения, число людей в автобусе, число страниц в книге.

Распределению Пуассона удовлетворяют вероятности появления заданного кол-ва редко происходящих случайных событий, наблюдаемый в серии из большого числа независимых опытов. Это распределение описывает дискретные, целочисленные неотрицательные случайные величины, появляющиеся с вероятностью р, много меньшей 1.

P_n(m)= /m!)* ,

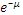Где m-число ожидаемых событий, P_n(m)-вероятность появления m искомых событий в серии из n независимых испытаний, μ-параметр распределения, совпадающий с математическим ожиданием, е-основание натурального логарифма.

Формулы для вычисления математического ожидания случайной величины.

Для дискретных величин M=∑Xi * Pi

Для непрерывных величин M=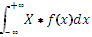

Формулы для вычисления дисперсии случайной величины, среднеквадратического отклонения

Для дискретных величин D=∑(Xi-Xср)² * Рi

Для непрерывных величин D= 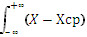² * f(x)dx

Среднеквадратическое отклонение δ=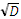

Вероятность

- предел, к которому стремится частота события при неограниченном увеличении числа испытаний. (статистическое определение)

P(A)=lim_n→∞(m/n)

- отношение благоприятствующих случаев к общему числу равновозможных случаев к общему числу равновозможных несовместимых событий. (классическое опредедение) P(A)=(m/n)

Распределение вероятностей — закон, описывающий область значений СВ и вероятности их принятия.

1. Распределение ДСВ. Дискретная величина (Х) считается заданной, если указаны ее возможные значения (x_n) соответствующие им вероятности Р(х_n)=p_n. Совокупность Х и Р называется распределением ДСВ.
2. Распределение НСВ.

dP=f(x)dx

dP – вероятность того, что НСВ Х принимает значения между х и х+dх. Вероятность dP прямо пропорциональна интервалу dx.

f(x) – плотность вероятности (функция распределения вероятностей). Показывает, как изменяется вероятность, отнесенная к интервалу dx случайной величины, в зависимости от самой этой величины.

f(x)=dP/dx

_x

F(x)=∫f(x)dx - функция распределения НСВ. Равна вероятности того, что СВ

^-∞

принимает значения, меньшие х.

F(x)=(-∞<X<x)

Нормальный закон распределения (закон Гаусса).СВ распределена по этому закону, если плотность вероятности имеет вид

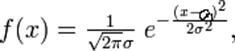
a=M(X) – мат.ожидание СВ, σ – среднее квадратическое отклонение, σ²- дисперсия СВ.

Дисперсия СВ – МО отклонения случайной величины от ее МО.

D(X)=M[X-M(X)]

Удобная формула: D(X)=M(X²)-[M(X)]²

Кривая закона носит колокообразную форму, симметричную относительно прямой х=а (центр рассеивания). В точке х=а функция достигает максимума.

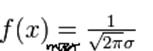
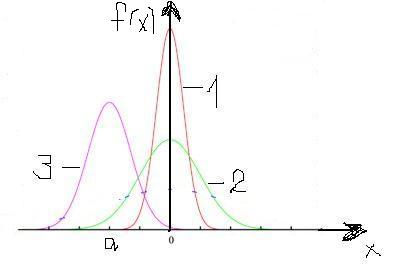
По мере возрастания |х-а| функция f(x) монотонно убывает, асимптотически приближаясь к нулю. С уменьшением σ кривая становится все более и более островершинной. Изменение а при постоянной σ не влияет на форму кривой, а лишь сдвигает ее вдоль оси абсцисс. Площадь, заключенной под кривой, согласно условию нормировки, равна единице. На рисунке изображены три кривые. Для кривых 1 и 2 а=0, но отличаются значением σ (σ₁<σ₂), кривая 3 имеет а≠0, σ=σ_2.

Вычислим функцию распределения.

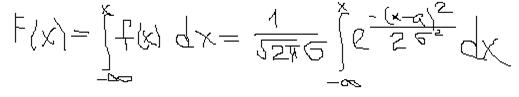
Обычно используют иное выражение. Введем новую переменную t=(x-a)/σ. Следовательно, dx=σdt. Подставляем это в формулу.

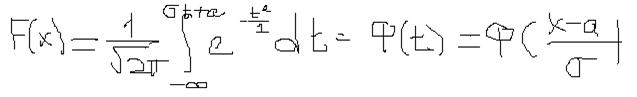
Значение функции Ф(t) обычно находят в составных таблицах, так как интеграл через элементарные функции не выражается. График:

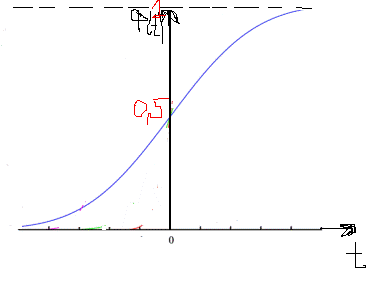
Случайная величина при нормальном распределении может находится в интервале (х₁, х₂). Вероятность этого равна

Р(х₁<x<х₂)=Ф((х₂-а)/σ)-Ф((х₁-а)/σ)

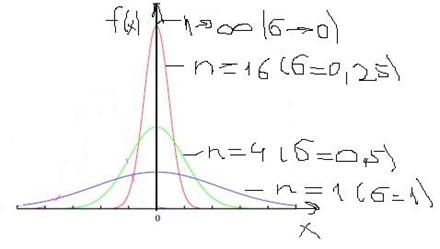
Допустим, что произвольно из нормальных распределений выбираются группы по n значений СВ. Для каждой группы можно найти средние значения (х₁, х₂, х_i). Они сами образуют нормальное распределение (только среднему значению будет соответствовать не вероятность, а относительная частота). МО будет соответствовать исходному, дисперсия и среднее квадратическое отклонение – отличаться в n и в √n соответственно.

D_n=D/n и σ_n=σ/√n.

На рисунке представлены графики нормальных распределений, полученных для групп со значением n, равными 1, 4, 16 и n→∞. При n=1 – исходное распределение, σ_n=σ. При n→∞ σ_n→0, фактически «группа СВ» - все исходное распределение, среднее значение выражается одним числом и соответствует МО, к которому сводится все распределение.

Стандартные интервалы

(вместо < должно быть </=)

1. М- σ <х< М+ σ (α = 68%)
2. М- 2σ <х< М+ 2σ (α = 95%)
3. М- 3σ <х< М+ 3σ (α = 99,7%)

Статистика 9. Понятие генеральной совокупности и выборки. Объём выборки, репрезентативность. Статистическое распределение (вариационный ряд). Примеры. Характеристики выборки

Основу статистического исследования составляет множество данных, полученных в результате измерения одного или нескольких признаков. Реально наблюдаемая совокупность объектов, статистически представленная рядом наблюдений случайной величины , является выборкой, а гипотетически существующая (домысливаемая) — генеральной совокупностью.

Пример. Практически одна и та же случайно отобранная совокупность объектов — коммерческих банков одного административного округа Москвы, может рассматриваться как выборка из генеральной совокупности всех коммерческих банков этого округа, и как выборка из генеральной совокупности всех коммерческих банков Москвы, а также как выборка из коммерческих банков страны и т.д.

Число наблюдений, образующих выборку, называется объемом выборки.

Репрезентативности выборки - полнота и адекватность свойств генеральной совокупности, по отношению к которой эту выборку можно считать представительной. Изучение статистических свойств совокупности можно организовать двумя способами: с помощью сплошного и несплошного наблюдения . Сплошное наблюдение предусматривает обследование всех единиц изучаемой совокупности, а несплошное (выборочное) наблюдение — только его части.

Выборка образует вариационный ряд, если выборочные значения случайной величины упорядочены по возрастанию (ранжированы), значения же признака называются вариантами.

Характеристики выборки:

Качественная характеристика выборки – кого именно мы выбираем и какие способы построения выборки мы для этого используем.

Количественная характеристика выборки – сколько случаев выбираем, другими словами объём выборки.

Выборочная средняя.

Пусть для изучения генеральной совокупности относительно количественного признака Х извлечена выборка объема n.

Выборочной средней называют среднее арифметическое значение признака выборочной совокупности.

Если все значения признака выборки различны, то

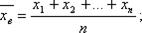
если же все значения имеют частоты n1, n2,…,nk, то

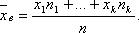
Выборочная средняя является несмещенной и состоятельной оценкой генеральной средней.

Генеральная дисперсия.

Для того чтобы охарактеризовать рассеяние значений количественного признака Х генеральной совокупности вокруг своего среднего значения, вводят сводную характеристику — генеральную дисперсию.

Генеральной дисперсией Dг называют среднее арифметическое квадратов отклонений значений признака генеральной совокупности от их среднего значения .

Если все значения признака генеральной совокупности объема N различны, то

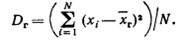
Если же значения признака имеют соответственно частоты N1, N2, …, Nk, где N1 +N2+…+Nk= N, то

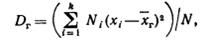
Кроме дисперсии для характеристики рассеяния значений признака генеральной совокупности вокруг своего среднего значения пользуются сводной характеристикой— средним квадратическим отклонением.

Генеральным средним квадратическим отклонением (стандартом) называют квадратный корень из генеральной дисперсии:

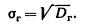
Выборочная дисперсия.

Для того, чтобы наблюдать рассеяние количественного признака значений выборки вокруг своего среднего значения , вводят сводную характеристику- выборочную дисперсию.

Выборочной дисперсией называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения .

Если все значения признака выборки различны, то

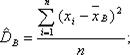
если же все значения имеют частоты n1, n2,…,nk, то

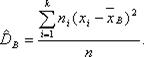
Для характеристики рассеивания значений признака выборки вокруг своего среднего значения пользуются сводной характеристикой - средним квадратическим отклонением.

Выборочным средним квадратическим отклоненим называют квадратный корень из выборочной дисперсии:

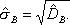
Вычисление дисперсии- выборочной или генеральной, можно упростить, используя формулу:

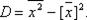
Замечание: если выборка представлена интервальным вариационным рядом, то за xi принимают середины частичных интервалов.

Статистика.

Вопрос.

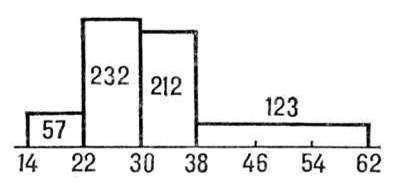
Гистограмма, столбчатая диаграмма, один из видов графического изображения статистического распределении каких-либо величин по количественному признаку. Г. представляет собой совокупность смежных прямоугольников, построенных на прямой линии. Площадь каждого прямоугольника пропорциональна частоте нахождения данной величины в изучаемой совокупности. Пусть, например, измерение диаметров стволов 624 сосен дало следующие результаты:

Диаметр, см

14—22

22—30

30—38

38—62

Число стволов

На горизонтальной оси откладываются границы групп, на которые стволы разбиты по их диаметру, и на отрезке, соответствующем каждой группе, строится как на основании прямоугольник с площадью, пропорциональной числу стволов, попавших в данную группу.

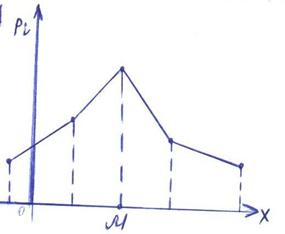
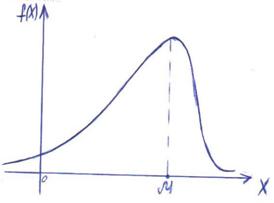
Модой случайной величины называется её наиболее вероятное значение. Термин «наиболее вероятное значение», строго говоря, применим только к прерывным величинам; для непрерывной величины модой является то значение, в котором плотность вероятности максимальна. На рис. А и Б показана мода соответственно для прерывной и непрерывной случайных величин.

а) б)

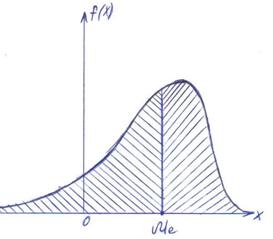
Часто применяется еще одна характеристика положения – так называемая медиана случайной величины. Этой характеристикой пользуются обычно только для непрерывных случайных величин, хотя формально можно её определить и для прерывной величины. Геометрически медиана – это абсцисса точки, в которой площадь, ограниченная кривой распределения, делится пополам.

Выборочной средней называют среднее арифметическое значение признака выборочной совокупности.

Если все значения признака выборки различны, то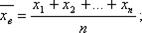

Если же все значения имеют частоты n1, n2,…,nk, то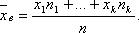

Критерий Стьюдента.

Статистика.

1.

Случайное событие – событие, которое в ходе испытании может произойти, а может и не произойти

Классическое определение вероятности:

Вероятностью Р(А) случайного события А называется отношение кол-ва m элементарных событий А к общему кол-ву элементарных событий n.

Р(А)=m/n

Статистическое определение вероятности:

Вероятность – это число Рст(А), около которого группируются значения относительной частоты р*(А) наступления случ.события А при неограниченном возрастании кол-ва испытаний

Совместные события (А1,А2,А3…). Осуществление любого из них в рез-те испытания не исключает осуществления при этом любого другого из перечисленных событий.

Несовместные события (А1,А2,А3…). Осуществление любого из событий в рез-те испытания исключает осуществление при этом других перечисленных событий.

Зависимое событие. На его вероятность оказывает влияние исход какого-либо иного события.

Независимое событие. Б независимо от А, если появление или не появление события А не влияет на вероятность события Б.

Статистика. Вопрос 2. Теоремы сложения и умножения вероятностей. Условные вероятности.

Теорема сложения: вероятность появления какого-либо события из нескольких несовместных равна сумме их вероятностей. P(A или B)=P(A)+P(B)

Теорема умножения: вероятность совместного появления независимых событий равна произведению их вероятностей. P(A и B)=P(A)*P(B)

Условная вероятность – вероятность некоторого события при условии того, что другое событие произошло, либо не произошло. Например, событие А произойдет при условии реализации события В. В таком случае используют обозначение Р(А/В).

Теорема умножения вероятностей для зависимых событий: вероятность наступления случайного события А и зависящего от него события В равна произведению вероятности события А на условную вероятность события В. P(A и B)=P(A)*P(B/А)