Доверительный интервал и доверительные вер-ти

Наряду с точечным оцениванием теория оценки пар-ов занимается вопросами интервального оценивания. Эту задачу можно сформулировать так: по данным выб-ки построить числовой интервал, относительно которого с заранее выбранной вероятностью м. сказать, что внутри этого интервала нах-ся оцениваемый пар-р. Интервальное оценивание особенно необх-мо при малом числе наблюдений, когда точечн. оценка малонадёжна. Доверительный интервал- отн-но него можно можно с заранее выбранной вер-ю р=1- 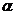близкой к ед-це утв-ть, что он содержит неизвестное значение пар-ра. Чем меньше этот интервал, тем точнее оценка неизвестного пар-ра и наоборот. Вероятность р=1- 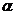-дов. вер-ть(ДВ), а 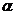-уровень значимости. Выбор ДВ не является матем-ой задачей, а опр-ся конкретной решаемой проблемой. Например, на двух п/п-ях вер-ть выпуска кач-ых изделий р=1- 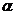=0, 99=> 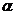=0,01. Нельзя в рамках мат. теории, не интересуясь хар-ом вып-ых изделий решить вопрос о том, мала или велика вер-ть 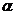. Одно п/п-ие выпускает кирпич, а другое-тормозные парашюты для самолётов. Если на 100 кирпичей встретится 1 брак, то это не страшно. Выбросить этот кирпич дешевле, чем усоверш-ть технологии. Если бракованный парашют, то…След-но, в превом случае вер-ть брака приемлима, во втором -.нет. На практике обычно принимают 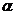=0,01 или 0,05.

Ошибки случайной выборки

Рассмотрим формулы ошибок выборки для случ. повторяющегося отбора, т.к.применительно к нему были впервые разработаны осн. положения выборочного метода. При случайном отборе каждая ед-ца имеет одинаковую вер-ть попасть попасть в выборку. Напр., имеем 4-х раб-х разной квал-ции:

Чем больше отклон-ся выборочная средняя от генер, тем меньше её вер-ть. В каждом случае выборки возникает ошибка (x с волной минус x с чертой), кот имеет туже вер-ть, что и выборочное среднее, плэтому возникает необходимость оценки выборочных данных. Различают среднюю и предельную ошибку выборки. Средняя ошибка выборки – есть среднее квадратич отклонение возможных значений выбор средней от генеральной. В мат ст-ке док-но, что дисперсия выборочной средней (µ² ) в n раз меньше дисперсии генер сов-ти, т е µ² = (G² генер / n) или µ = G / √n. µ =√ (G² генер / n), но G² генер не = G² выбор. G² генер не = G² выбор * n / (n-1). Но при большом значении n сомножитель n/(n-1) близок к 1, поэтому принмают, что G² генер приблизительно = G² выбор, следовательно, ошибка выборки явл-ся приблизительной. Фактическое расхождение между выбор средней и генер по абсолютной величине / x c волной минус x с чертой/ можно рассматривать, как некую предельную ошибку, связанную с µ, и гарантирует с определенной вер-тью P. Предельная ошибка ∆ = µ*t, где µ - ср ошибка выборки, t – коэф доверия, или кратности ошибки, завис от вер-ти опред предельн ошибки.

В теории Чебышева док-но, что при большом числе наблюдений разность между выборочной средней и генеральной будет небольшой, однако мы не можем указать вер-ть появления ошибок определенной величины. Эта неопред-ть была устранена Ляпуновым. Он док-л, что при большом числе наблюдений и огранич дисперсии вер-ть того, что расхождение между выборочн и генер средней не превзойдёт по абсол величине µ*t = интегралу Лапласа, значения которого рассчитаны и даются в спец-х таблицах. Вер-ть появления ошибки больше утроенной средней ошибки выборки крайне мала, поэтому ∆ = 3µ пожно принять за предел возможной ошибки выборки. Рассмотренные формулы применимы для опред ошибок выборки альтернат-х признаков, те е наличие признака (1) или его отсутствие (0). Теорема Бернилли утверждает, что при достат большом объёме выборки вер-ть расхождения между долей признака выбор сов-ти (w) и долей признака в генер сов-ти (p) будет стремиться к 1.P[/w – p/≤µ*t]→1. Поскольку µ = G / √n, а ср квадрат отклон генер сов-ти для альтернат признака = √(pq), где q=1-p, то ср ошибка для альтернат признака µ = √(pq/n), а ср ошибка для доли признака µ = √(w(1-w)/n). Все приведённые формулы ошибок выборки рассм-сь применительно к повторному отбору, но чаще примен-ся бесповторный отбор (меньше ошибка), поэтому для него в подкоренное выражение ввод дополнит сомножитель (N-n)/(N-1) или 1-n/N. Если пренебречь единицей при больших значения N, этот множитель всегда < 1, то очевидно, что предельная ошибка выб песповторного отбора будет меньше, чем при повторном отборе.