Правила построения относительных величин.

1) Относительные величины надо рассматривать тесной связи с абсолютными величинами, на базе которых они рассчитаны.

2) Необходимо обеспечить сопоставимость статистических показателей по территории времени единицы измерения.

№2

Наиболее распространенной формой статистических показателей, используемых в социально-Экономических исследованиях, является средняя величина, представляющая собой количественную характеристику признака статистической совокупности в конкретных условиях места и времени. Показатель в форме средней величины выражает типичные черты и дает обобщающую характеристику однотипных явлений по одному из варьирующих признаков. В средних величинах погашаются индивидуальные различия единиц совокупности, обусловленные случайными обстоятельствами.

Виды средних величин.

1.Средняя арифметическая простая – применяется в тех случаях, когда имеется значения признака по каждой единицы совокупности или когда каждое значение признака встречается одинаковое число раз. В статистике изучение изучаемого признака называются вариантами и обозначаются Х1..Хn.

Х̄̄=(Х1+..+Хn)/n n – число вариантов

2.среднее арифметическое взвешенное - исчисляется, когда значение признака встречается не одинаковое число раз или по сгруппированным данным.

Х̅=(Х1*f1+…+Хn*fn)/(f1+..+fn)

3.Средне гармоническая- представляет собой обратную величину средней арифметической из обратных величин. Применяется в тех случаях, когда имеются данные об индивидуальных значениях усредняемого признака и общем объеме совокупности, но не известные чистоты или веса(f)

X̅=∑W/∑(W/x) где Wi=Xi*fi выручка, цена, кол-во.

4.Средняя хронологическая – применяется в рядах динамики.

X̅=(1/2*X1+X2+X3+..+1/2Xn)/n-1

5.Средняя геометрическая – также используется в рядах динамики и так же как средне арифметическая может быть просто и взвешенной.

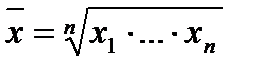
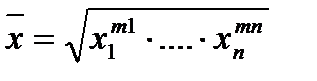
6.Средняя квадратическая -применяется при расчете показателей вариации.

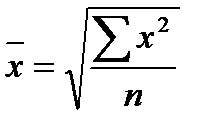
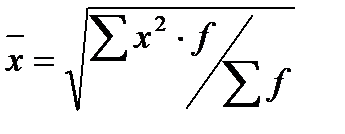
7. Структурная среднее: мода и медиана.

Мода– модой называется наиболее часто встречающаяся величина признака. В интервальном вариационном ряду формула моды выглядит следующим образом.

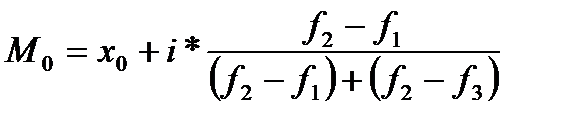
Где х0-нижняя граница модального интервала(модальный-интервал с наибольшей численностью)

i-величина интервала

F1 – величина интервала предшествующая…

F2- чистота модального интервала

F3 –чистота интервала следующего за модальным интервалом.

(таблица)

Медианой называется величина признака, которая находится в середине упорядоченного вариационного ряда. Где варианты расположены в порядке возрастания или убывания, если число членов ряда нечетное медианой будет средний член ряда по порядку.

Если число членов ряда четное медианой является среднее арифметическая простая из двух вариант находящихся в середине ряда.

В случае интервальных вариационных рядов, медиана рассчитывается по формуле:

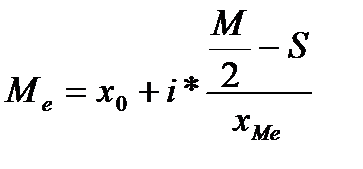
Гдех0-нижняя граница медианного интервала

i-величина медианно интервала

М- численность всех совокупности

S - сумма накопленных частот интервалов предшествующих медианному.

Хме- чистота медианного интервала.

Для того что бы определить в каком интервале находится медиана необходимо найти сумму накопленных частот интервалов превосходящую половину численности совокупности. Численность совокупности это число объектов, которые мы подвергаем исследованию.

Главное свойство медианы заключается в том, что сумма абсолютных отклонений значений признака от медианы меньше чем от другой любой величины. Если мода отражает типичный наиболее распространенный вариант значений признака, то медиана практически выполняет функции средней для неоднородной совокупности .Она так же используется, когда среднее не позволяет оценить исследуемую совокупность в следствии сильного влияния максимальных минимальных значений.

№3Средняя арифметическая сама по себе не достаточно для обобщающей характеристики совокупности. В средней отражаются общие условия присущие всей данной совокупности, но не отражаются индивидуальные частные условия порождающие вариацию отдельных единиц совокупности.

Вариация - отклонение индивидуальных значений от средней. Для обобщающей характеристики колеблимости или вариаций используют следующие показатели: размах вариаций, средние линейные отклонения, среднее квадратическое отклонение, дисперсия, и коэффициент вариаций.

Размах вариаций представляет собой разность между наибольшим и наименьшим значениями признака R=Xmax-Xmin.

Средние линейные отклонения представляют собой среднею из абсолютных величин отклонений всех значений от их средней арифметической.

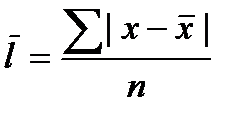простая

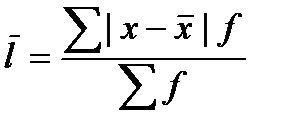взвешенная f-веса

n-число вариантов.

Среднее квадратическое отклонения представляет собой корень квадратный из дисперсии.

Дисперсия- средний квадрат отклонений индивидуального значения признака от их средней величины.

Среднее квадратическое отклонение так же как среднее линейное отклонение рассчитывается по простой или взвешенной формуле, выбор которой зависит от способа расчета средней арифметической

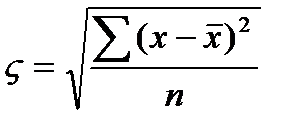
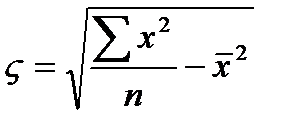
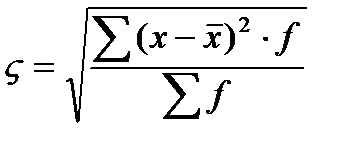средняя квадратическая взвешенная

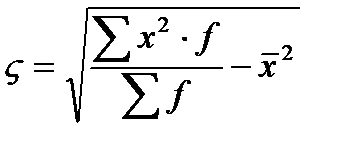
(если расчет дисперсии)

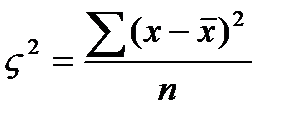
Среднее квадратическое отклонение показывает абсолютную меру колеблимости признака в тех же единицах измерения, что и средней величины, но оно не может служить для сравнения показателей колеблимости по различным совокупностям с этой целью используют следующий показатель коэффициент вариаций, который представляет собой отношения среднего квадратического отклонения к средней арифметической.

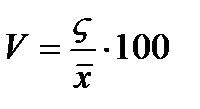выражается в процентах.

Если значение коэффициента вариаций меньше 33 % то совокупность по рассматриваемому признаку можно считать однородной.

№4

Показатели вариаций могут быть использованы не только в анализе колеблемости изучаемого признака, но и в оценки степени воздействия одного признака на вариацию другого признака, то есть в анализе взаимосвязей между показателями. При проведении такого анализа исходная совокупность должна представлять собой множество единиц каждая из которых характеризуется двумя признаками: факторным и результативным.

Факторнымназывается признак оказывающий влияние на взаимосвязанный с ним признак. Признак, поддержанный влиянию, называется результативным.

Для выявления взаимосвязи исходная совокупность делится на две и более групп по факторному признаку. Выводы о степени взаимосвязи базируются на анализе вариации результативного признака, при этом применяется правило сложения дисперсий.

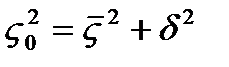общая дисперсия, средняя из внутригрупповых дисперсий, межгрупповая дисперсия(дельта).

Средняя из внутри групповых дисперсий выражает ту часть вариаций результативного признака, которая обусловлена действием всех прочих неучтенных факторов. Кроме фактора по которому осуществлялась группировка.

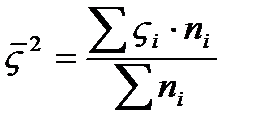колебания среднего р. рабочих активов= дисперсия результативности признака в i-той группе, ni – объем или численность.

Межгрупповая дисперсия отражает, ту часть вариаций результативного признака, которая обусловлена воздействием факторного признака. Это воздействие проявляется в отклонении групповых средних от общей средней.

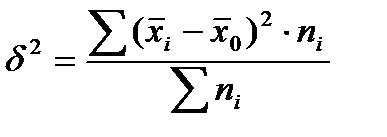
x̅i-среднее значение результативного признака i-той группе

x̅0- среднее значение результативного признака по совокупности в целом (общее среднее)

ni- объем или численность i- той группе

Если факторный признак, по которому производилась группировка не оказывает никакого влияния на результативный признак групповые средние будут равны между собой и совпадут с общей средней. В этом случае межгрупповая дисперсия будет равно нулю.

Теснота связи между факторным и результативным признаками оценивается на основе эмпирического корреляционного отношения.

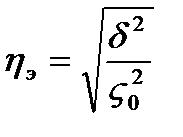
Данный показатель может принимать значения от 0 до 1, чем ближе к единице будет его величина, тем сильнее связь между рассматриваемыми признаками.

Ряды распределения представляют собой простейшую группировку, в которой каждая выделенная группа характеризуется одним показателем.

Статистический ряд распределения это упорядоченное распределение единиц совокупности на группы по определенному варьирующему признаку. В зависимости от признака положенного в основу ряда распределения различают атрибутивные(не имеют количественного выражении) и вариационные ряды распределения.

Вариационные рядами называют ряда распределения, построенные по количественному признаку. В зависимости от характера вариаций признака различают дискретные и интервальные вариационные ряды.

Дискретный вариационный ряд характеризуют распределения по дискретному признаку, принимающему только целые значения. (количество детей, 0,1,2,3)

Построение интервальных вариационных рядов целесообразно, прежде всего, при непрерывной вариации признака, а так же если дискретная вариация проявляется в широких пределах, то есть число вариантов дискретного признака достаточно велико.

Правило построения рядов распределения аналогичны правилам построения группировки.

Анализ рядов распределения наглядно можно проводить на основе графического изображения: полигон – этот график используется для дискретных рядов. (8 график)

Гистограмма- строится для интервальных рядов.

Кумулята – график накопленных частот. (9 график)

Огива – график схожий с кумулятой, если у кумуляты поменять местами оси X и Y.

При проведении группировки можно заметить определенную зависимость между изменений значений варьирующего признака и частот. Частоты с увеличением значений варьирующего признака первоначально увеличиваются, а затем после достижения максимальной величины середины ряда уменьшаются. Такие закономерности изменения частот в вариационных рядах называются закономерностями распределения.

(10график)

Под кривой распределения понимается графическое изображение в виде непрерывной линии изменений частот в вариационном ряду, функционально связанного с изменением вариантов.

В статистической практике встречаются следующие разновидности кривых распределения.

1.одновершинные кривые, которые могут быть семетричными , умеренно асиметричными и крайне ассиметричными.

2.Многовершинные кривые.

Для однородных совокупностей, как правило характерны одновершинные распределения. Многовершинность свидетельствует о неоднородности совокупности и в таком случае необходимо перегруппировка данных с целью выделения более однородных групп.

Выяснения общего характера распределения предполагает оценку его однородности, а так же вычисления показателя асимметрии. Для симметричных распределений частоты любых двух вариант равно отстоящих в обе стороны от центра распределения равны между собой, а так же равны среднее, мода и медиана. Х=М0=Ме

При сравнительном изучении асимметрий нескольких распределений с разными единицами измерения вычисляется относительный показатель асимметрии.

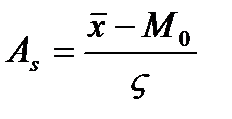
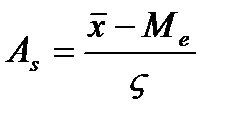
Если коэффициент асимметрии положительный имеет место правосторонняя асимметрия, если отрицательный – левосторонний. Если коэффициент асимметрии больше 0,5 независимо от знака – асимметрия значительна. Если меньше 0,25 асимметрия не значительна.

Выборочное наблюдение

1. Основные теоретические положения выборочного метода.

2. Виды выборки.

3. Ошибки выборочного наблюдение и их вычисления.

4. Определения необходимой численности выборки.

5. Оценка результатов выборочного наблюдения и распространение на генеральную совокупность.

6. Малая выборка.

№1

Выборочным называется такое наблюдение, которое дает характеристику всей совокупности на основе обследования некоторые ее части. Выборочный способ имеет ряд преимуществ перед сплошным.

1. необходимые сведения нужно получить с меньшими затратами материальных средств.

2. меньше затрат рабочего времени.

3.В ряде случаев статистическое наблюдение можно провести только путем выборочного обследования.

При выборочном способе допускается меньше ошибок регистрации. При проведении выборочного обследования необходимо соблюдать следующие положения.

1. Для каждой единицы должна обеспечиваться равная возможность попасть в выборку.

2. численность выборки должна быть достаточно большой, что бы результаты были надежными. Причем достаточно большой считается 10% выборка.

При выборочном наблюдении анализируют генеральную и выборочную совокупность.

Генеральной совокупностью называется общая масса единиц данного рода из которой производят отбор некоторой части для обследования.

Выборочная совокупность представляет собой массу единиц данного рода, отобранных из генеральной совокупности для выборочного обследования.

Выборочные наблюдения широко используются во первых для статистической оценки и проверки гипотез, то есть применяется в науке. Во вторых, для решения производственных и управленческих задач. 3.при отраслевых социально-экономических исследований. 4.для решения задач сфере предпринимательской деятельности.

№2

В зависимости от способа отбора различают следующие виды выборочного наблюдения.

1.собственно случайное наблюдение

2.механическое

3.типическое

4.серийное

Причем все они могут быть повторными и без повторными.

Повторным называется отбор, при котором ранее отобранные единицы после записи ее признаков возвращаются в генеральную совокупность и снова участвуют в выборки.

Без повторный это способ отбора, при котором ранее отобранная единица больше не возвращается в генеральную совокупность и в дальнейшей выборке не участвует.

1)Собственно случайно называется отбор, при котором каждая единица имеет равную возможность попасть в выборку. При этом формирование выборочной совокупности чаще всего производится путем жеребьевки. Однако применение жеребьевки связано с значительными затратами, кроме того не всегда возможно заранее составить перечень единиц совокупности, поэтому применяют один из следующих способов.

2) механический отбор, представляет собой разновидность случайного отбора заключается в том что отбор единиц производится в каком либо механическом порядке.

3) типическим называется отбор, при котором генеральная совокупность предварительно разбивается на более или менее однородные группы, из которых в случайном порядке производят отбор необходимой численность единиц, либо случайным либо механическим способом, но при этом важно соблюдать пропорции.

4) серийным называется такой отбор, при котором единица совокупности забираются сериями, а внутри серии проводится сплошное обследование.

На практике различные виды выборочного наблюдения используется не в чистом виде, а в различных сочетаниях(напрмер, случайные и механические) . Таким образом, получаем комбинированный отбор.

Многоступенчатый отбор, когда их генеральной совокупности сначала извлекаются укрупненные группы, затем более мелкие и так до тех пор пока не будут отобраны те единицы , которые подвергаются обследованию.

№3

Ошибки репрезентативности свойственны только выборочному наблюдению и представляют собой величину расхождения между сводными показателями генеральной и выборочной совокупности.