Понятие вариации, показатели вариации.

Показатели вариации

Вариация - различия в индивидуальных значениях признака у единиц совокупности. Наличие вариации и вызывает саму необходимость стат изучения соц-экономических явлений.

Существуют 2 типа показателей вариации:

1 абсолютные

1.1 Размах вариации

R=Xmax-Xmin

Разность между max и min значениями признака.

Он характеризует границы существования признаков совокупности. Прежде чем рассчитывать этот показатель надо оценить изучаемую совокупность на наличие выбросов и может исказить величину этой характеристики.

1.2 Среднее линейное отклонение

d= (Σ |‌‌‌‌‌‌‌‌Xi-X|)/n (по средней арифмет простой)

d= (Σ |Xi - X| fi) / Σ fi (по средней арифмет взвешенной)

Xi- индивидуальные значения признака

1.3 Дисперсия

G² = (Σ (Xi- X) ² fi) / Σ fi ( по средн квад-й)

1.4 Среднее квадратическое

G =√G² = √ (Σ (Xi - X)² fi) / Σ fi

‌Вышеперечисленные показатели, именованные величины измеряются в тех же единицах что и показатель вариации кот изучается.

Показатель дисперсия содержательно не интерпретируется, но используется во многих методах стат. анализа.

В нормально распределенных совокупностях между показателями средняя линейная и средняя квадратическая существует следующее соотношение: G= 1.250 t

Соотношение этих показателей рассчитанных по анализируемой совокупности позволяет предположить наличие или отсутствие эмпирического распределения нормальному.

В нормально распределенной совокупности существуют следующие соотношения между величиной среднего квадратического и числом единиц совокупности.

X+ 1G→68.3%

X+ 2G→95.4%

X+ 3G→99.7%

Это соотношение получило название трех сигм (3-x G) Суть: в совокупности распределения кот соответствует закону нормального распределения, практически не встречаются отклонения превышающие величину 3-х G.

X = 20000

G=1500

3G=4500

18500-21500

15500-24500- предельные изменения признаков совокупности

На основе абсолютных показателей вариации нельзя сравнить степень вариации разных признаков в пределах одной совокупности, а также вариацию одного и того же признака по разным степеням.

2 относительные

Рассчитываются как отношение абсолютных показателей вариации к средней величине по совокупности.

2.1 Коэффициент

Kr= R/X

2.2 Относительное линейное отклонение

Kd= d /X

2.3 Коэффициент вариации

V=G/X

Наиболее аналитические значения имеет коэф вариации. Он чаще всего выражается в %, если он меньше 33 % изучаемая совокупность признается количественно однородной т. е степень разброса значений признака не существенный, если более 33 % совокупность признается неоднородной разброс значений существенный.

Правило сложения дисперсий

Особенности отбора ошибки выборки при различных видах выборки.

Правило сложения дисперсий использ. Разные виды дисперсий при расчете различных видов выборки.

Правило сложения дисперсий : общая дисперсия это сумма межгрупповой 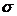и внутригрупповой .

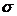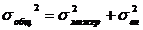
Все виды дисперсии могут быть рассчитаны по аналитической группировке.