Виды статистических показателей

Статистические показатели

Сложный характер социально-экономических явлений диктует необходимость расчета системы взаимосвязанных и взаимодополняющих показателей.

Выделяют группы:

1. абсолютные
2. относительные
3. средние величины

АБСОЛЮТЫЕ – показатели характеризующие объем совокупности или отдельных ее типов и групп, а так же объем признака в совокупности или группах.

Первые получаются путем суммирования единиц совокупности, вторые – суммированием значений признаков.

Всегда именованные величины. Несут определенную аналитическую нагрузку, а так же являются базой для расчета относительных и средних характеристик.

ОТНОСИТЕЛЬНЫЕ – м.б. получены путем сопоставления одноименных относительных величин. В результате получаются следующие показатели: показатель динамики, показатель структуры(отношение части к целому), показатель планового задания и выполненного плана, относительный показатель координации(сопоставление частей одного целого), показатель наглядности(сопоставление одноименных показателей в производстве).

Все перечисленные относительные показатели не именованные относительно величины. При сопоставлении разноименных абсолютных величин получают относительный показатель – показатель интенсивности, который характеризует степень распространенности (показатель уровня жизни населения, обеспеченности товарами) – именованные величины.

(8. Типы средних)СРЕДНИЕ ВЕЛИЧИНЫ: необходимо рассчитать средние характеристики обусловленные природой социально-экономических явлений. С одной стороны они устойчивы в массе, с другой стороны – сугубо индивидуальны. Это связано с тем, что формируются они под влиянием множества факторов. Одни из факторов называются основными – определяют типический, характерный для совокупности признак. Другие, случайные факторы, формируют отклонение отдельных значений этого типического уровня. В средних величинах происходит взаимопогашение отклонений, и поэтому средние значения характеризуют типический уровень признака в случайной совокупности. Отражают типический уровень только при условии, что они рассчитаны по однокачественной совокупности явлений и при решении ряда задач необходимым условием является количественная однородность изучаемой совокупности. Средние показатели рассчитываются на единицу совокупности, но характеризуют совокупность в целом. Китле: «Статистические средние представляют собой категорию объективной действительности. Типическое среднее – это истинная величина, отклонение о которой может быть только случайным».

Средние величины м.б. 2-х видов:

1. структурное среднее
2. степенные средние

2-среднее арифметическое, среднее гармоническое, среднее геометрическое, среднее квадратичное.

1-мода и медиана, т.к. их величина не зависит от значения признака по каждой единицы совокупности, а представлена составом(структурой) изучаемой совокупности.

Средняя арифметическая простая:

Таким образом средняя арифметическая это отношение объема признака к объему совокупности. Используется при расчете средних показателей по абсолютным, не сгруппированным данным.

Средняя арифметическая взвешенная:

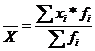
f_i – вес или частота, характеризует как часто в совокупности встречается то или иное значение признака

Среднее арифметическое взвешенное используется при расчете средних характеристик по сгруппированным показателям, а так же для определения средних значений по относительным величинам, при условии, что известен знаменатель исходной формулы усредняемого показателя.

Среднее гармоническое:

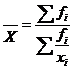
Средне гармоническая величина используется для характеристики типического значения, рассчитанного по относительным показателям, при условии, что известен числитель исходной формулы усредняемого показателя.

Среднее геометрическое:

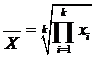k - число сомножителей подкоренного выражения

Используется в анализе рядов динамики при расчете средних темпов роста.

Среднее квадратическое:

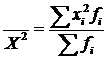
Свойства средней арифметической:

1. Произведение средней арифметической на сумму частот = сумме произведений индивидуальных значений на соответствующие частоты (Средняя арифметическая величина – это значение признака, которым обладала бы каждая единица совокупности, если бы V признака был равномерно распределен в изучаемой совокупности).

2. Сумма отклонений индивидуального значения признака от средней величины всегда =0

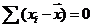Сумма отклонений с “+” и “-” равные

3. Сумма квадратов отклонений индивидуальных значений от средний величины всегда меньше суммы квадратов отклонений индивидуального значения от любой другой положительной величины.

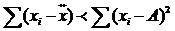
4. Если все значения в совокупности меньше или больше на одну и ту же величину, то средняя арифметическая изменится на эту же величин.

5. Если все частоты или веса меньше или больше на одну и ту же величину средняя арифметическая не изменится.