Изучение вариации признака в совокупности

Вариация - это различие в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период или момент времени. Она возникает в результате того, что индивидуальные значения признака складываются под совокупным влиянием разнообразных факторов (условий), которые по-разному сочетаются в каждом отдельном случае. Таким образом, величина каждого варианта объективна.

К показателям вариации относятся: размах вариации, среднее линейное отклонение, дисперсия и среднее квадратическое отклонение, коэффициент вариации.

Самым элементарным показателем вариации признака является размах вариации , представляющий собой разность между максимальным и минимальным значениями признака:

.

Среднее линейное отклонение и представляет собой среднюю арифметическую абсолютных значений отклонений отдельных вариантов от их средней арифметической (при этом всегда предполагают, что среднюю вычитают из варианта: ( ).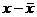

Среднее линейное отклонение:

для несгруппированных данных , (5.18)

где 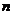- число членов ряда;

для сгруппированных данных , (5.19)

где 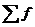- сумма частот вариационного ряда.

Среднее линейное отклонение как меру вариации признака применяют в статистической практике редко (только в тех случаях, когда суммирование показателей без учета знаков имеет экономический смысл).

Дисперсия признака представляет собой средний квадрат отклонений вариантов от их средней величины, она вычисляется по формулам простой и взвешенной дисперсий ( в зависимости от исходных данных):

простая дисперсия для несгруппированных данных

; (5.20)

взвешенная дисперсия для вариационного ряда

(5.21)

Формула (5.21) применяется при наличии у вариантов своих весов (или частот вариационного ряда).

Дисперсия имеет большое значение в экономическом анализе. В математической статистике важную роль для характеристики качества статистических оценок играет их дисперсия. Далее, в частности, будет показано разложение дисперсии на соответствующие элементы, позволяющие оценить влияние различных факторов, обуславливающих вариацию признака; использование дисперсии для построения показателей тесноты корреляционной связи при оценке результатов выборочных наблюдений.

Среднее квадратическое отклонение равно корню квадратному из дисперсии:

для несгруппированных данных , (5.24)

для вариационного ряда . (5.25)

Среднее квадратическое отклонение - это обобщающая характеристика размеров вариации признака в совокупности; оно показывает на сколько в среднем отклоняются конкретные варианты от их среднего значения; является абсолютной мерой колеблемости признака и выражается в тех же единицах, что и варианты, поэтому экономически хорошо интерпретируется.

Чем меньше значение дисперсии и среднего квадратического отклонения, тем однороднее (количественно) совокупность и тем более типичной будет средняя величина.

Для осуществления сравнений колеблемости одного и того же признака в нескольких совокупностях с различным средним арифметическим используют относительный показатель вариации - коэффициент вариации.

Коэффициент вариации представляет собой выраженное в процентах отношение среднего квадратического отклонения к средней арифметической:

. (5.30)

Коэффициент вариации используют не только для сравнительной оценки вариации единиц совокупности, но и как характеристику однородности совокупности. Совокупность считается количественно однородной, если коэффициент вариации не превышает 33 %.

Правило сложения дисперсий

Вариация признака обусловлена различными факторами, некоторые из этих факторов можно выделить, если статистическую совокупность разбить на группы по какому-либо признаку. Тогда, наряду с изучением вариации признака по всей совокупности в целом, становится возможным изучить вариацию для каждой из составляющих ее группы, а также и между этими группами. В простейшем случае, когда совокупность расчленена на группы по одному фактору, изучение вариации достигается посредством исчисления и анализа трех видов дисперсий: общей, межгрупповой и внутригрупповой.

Общая дисперсия измеряет вариацию признака по всей совокупности под влиянием всех факторов, обусловивших эту вариацию. Она равна среднему квадрату отклонений отдельных значений признака 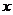от общей средней 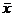и может быть вычислена как простая дисперсия или взвешенная дисперсия.

Межгрупповая дисперсия характеризует систематическую вариацию результативного порядка, обусловленную влиянием признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений групповых (частных) средних , от общей средней :

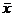, (5.31)

где 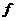- численность единиц в группе.

Внутригрупповая (частная) дисперсия , отражает случайную вариацию, т.е. часть вариации, обусловленную влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений отдельных значений признака внутри группы 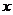от средней арифметической этой группы , (групповой средней) и может быть исчислена как простая дисперсия или как взвешенная дисперсия по формулам, соответственно:

; (5.32)

. (5.33)

На основании внутригрупповой дисперсии по каждой группе, т.е. на основании можно определить общую среднюю из внутригрупповых дисперсий:

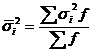. (5.34)

Согласно правилу сложения дисперсий общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий:

. (5.35)

Пользуясь правилом сложения дисперсий, можно всегда по двум известным дисперсиям определить третью - неизвестную, а также судить о силе влияния группировочного признака.

Очевидно, чем больше доля межгрупповой дисперсии в общей дисперсии, тем сильнее влияние группировочного признака (квалификашюнного разряда) на изучаемый признак (количество изготавливаемых изделий).

Поэтому в статистическом анализе широко используется эмпирический коэффициент детерминации ( )- показатель, представляющий собой долю межгрупповой дисперсии в общей дисперсии результативного признака и характеризующий силу влияния группировочного признака на образование общей вариации:

. (5.36)

Эмпирический коэффициент детерминации показывает долю вариации результативного признака 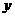под влиянием факторного признака 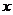(остальная часть общей вариации 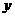обуславливается вариацией прочих факторов). При отсутствии связи эмпирический коэффициент детерминации равен нулю, а при функциональной связи - единице.

Эмпирическое корреляционное отношение - это корень квадратный из эмпирического коэффициента детерминации:

,

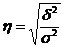оно показывает тесноту связи между группировочным и результативным признаками.

Эмпирическое корреляционное отношение , как и , может принимать значения от 0 до 1.

Если связь отсутствует, то корреляционное отношение равно нулю, т.е. все групповые средние будут равны между собой, межгрупповой вариации не будет. Значит, группировочный признак никак не влияет на образование общей вариации.

Если связь функциональная, то корреляционное отношение будет равно единице. В этом случае дисперсия групповых средних равна общей дисперсии ( ), т.е. внутригрупповой вариации не будет. Это означает, что группировочный признак целиком определяет вариацию изучаемого результативного признака.

Чем значение корреляционного отношения ближе к единице, тем теснее, ближе к функциональной зависимости связь между признаками.

Для качественной оценки тесноты связи на основе показателя эмпирического корреляционного отношения можно воспользоваться соотношениями Чэддока:

0,1-0,3 0,3-0,5 0,5-0,7 0,7-0,9 0,9-0,99

Сила Слабая Умеренная Заметная Тесная Весьма тесная

связи

Выборочное наблюдение

Выборочное наблюдение - это такое несплошное наблюдение, при котором отбор подлежащих обследованию единиц осуществляется в случайном порядке, отобранная часть изучается, а результаты распространяются на всю исходную совокупность.

Наблюдение организуется таким образом, что эта часть отобранных единиц в уменьшенном масштабе репрезентирует (представляет) всю совокупность.

Совокупность, из которой производится отбор, называется генеральной, и все ее обобщающие показатели - генеральными.

Совокупность отобранных единиц именуют выборочной совокупностью, н все ее обобщающие показатели - выборочными.

Принципы выборочного наблюдения:

- обеспечение случайности (равной возможности попадания в выборку) отбора единиц

- достаточное число единиц выборочной совокупности

Основная задача выборочного наблюдения в экономике состоит в том, чтобы на основе характеристик выборочной совокупности (средней и доли) получить достоверные суждения о показателях средней и доли в генеральной совокупности.

Ошибки репрезентативности присущи только выборочному наблюдению и возникают в силу того, что выборочная совокупность не полностью воспроизводит генеральную. Они представляют собой расхождение между значениями показателей, полученных по выборке, и значениями показателей этих же величин, которые были бы получены при проведенном с одинаковой степенью точности сплошном наблюдении, т.е. между величинами выборных и соответствующих генеральных показателей.

По методу отбора различают повторную и бесповторную выборки.

При повторной выборке общая численность единиц генеральной совокупности в процессе выборки остается неизменной.

Ту или иную единицу, попавшую в выборку, после регистрации снова возвращают в генеральную совокупность, и она сохраняет равную возможность со всеми прочими единицами при повторном отборе единиц вновь попасть в выборку ("отбор по схеме возвращенного шара"). Повторная выборка в социально-экономической жизни встречается редко. Обычно выборку организуют по схеме бесповторной выборки.

При бесповторной выборке единица совокупности, попавшая в выборку, в генеральную совокупность не возвращается и в дальнейшем в выборке не участвует; т.е. последующую выборку делают из генеральной совокупности уже без отобранных ранее единиц ("отбор по схеме невозвращенного шара").

По степени охвата единиц совокупности различают большие и малые (п<30) выборки.

Основные характеристики параметров генеральной и выборочной совокупностей обозначаются символами:

N - объем генеральной совокупности (число входящих в нее единиц);

_ n - объем выборки (число обследованных единиц);

х - генеральная средняя (среднее значение признака в 0 2генеральной совокупности);

~

х - выборочная средняя;

р - генеральная доля (доля единиц, обладающих данным значением признака в общем числе единиц генеральной совокупности);

w - выборочная доля;

s²- генеральная дисперсия (дисперсия признака в генеральной совокупности);

S²- выборочная дисперсия того же признака;

s- среднее квадратическое отклонение в генеральной совокуп-

ности;

S - среднее квадратическое отклонение в выборке.

При случайном повторном отборе средние ошибки теоретически рассчитывают по следующим формулам:

для средней количественного признака

для доли (альтернативного признака)

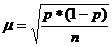
Поскольку практически дисперсия признака в генеральной совокупности s² точно неизвестна, на практике пользуются значением дисперсии S² , рассчитанным для выборочной совокупности на основании закона больших чисел, согласно которому выборочная совокупность при достаточно большом объеме выборки достаточно точно воспроизводит характеристики генеральной совокупности. В теории вероятностей доказано, что генеральная дисперсия выражается через выборную следующим соотношением:

Так как n/(n -1) при достаточно больших n - величина, близкая к единице, то можно принять, что , а следовательно, в практических расчетах средних ошибок выборки можно использовать формулы (6.5) и (6.6).

При случайном бесповторном отборе в приведенные выше формулы расчета средних ошибок выборки необходимо подкоренное выражение умножить на (1 - (n/N)), поскольку в процессе бесповторной выборки сокращается численность единиц генеральной совокупности.

Следовательно, для бесповторной выборки расчетные формулы средней ошибки выборки примут такой вид:

для средней количественного признака

для доли (альтернативного признака)

Так как n всегда меньше N, то дополнительный множитель (1 -(n/N) всегда будет меньше единицы. Отсюда следует, что средняя ошибка при бесповторном отборе всегда будет меньше, чем при повторном. В то же время при сравнительно небольшом проценте выборки этот множитель близок к единице ( например, при 5 %-ной выборке он равен 0,95; при 2 %-ной - 0,98 и т.д.). Поэтому иногда на практике пользуются для определения средней ошибки выборки формулами без указанного множителя, хотя выборку и организуют как бесповторную. Это имеет место в тех случаях, когда число единиц генеральной совокупности неизвестно или безгранично, или когда n очень мало по сравнению с N, и по существу, введение дополнительного множителя, близкого по значению к единице, практически не повлияет на значение средней ошибки выборки.

Выборочные средние и относительные величины распространяют на генеральную совокупность с учетом предела их возможной ошибки.

В каждой конкретной выборке расхождение между выборочной средней и генеральной может быть меньше средней ошибки выборки ц., равно ей или больше ее.

Причем каждое из этих расхождений имеет различную вероятность (объективную возможность появления события). Поэтому фактические расхождения между выборочной средней и генеральной можно рассматривать как некую предельную ошибку, связанную со средней ошибкой и гарантируемую с определенной вероятностью Р.

Предельную ошибку выборки для средней при повторном отборе можно рассчитать по формуле:

где t - нормированное отклонение - "коэффициент доверия", зависящий от вероятности, с которой гарантируется предельная ошибка выборки;

m - средняя ошибка выборки.

Аналогичным образом может быть записана формула предельной ошибки выборки для доли при повторном отборе:

При случайном бесповторном отборе в формулах расчета предельных ошибок выборки необходимо умножить подкоренное выражение на (1 - (n/N)).

Формула предельной ошибки выборки вытекает из основных положений теории выборочного метода, сформулированных в ряде теорем теории вероятностей, отражающих закон больших чисел.

На основании теоремы П.Л.Чебышева (с уточнениями А.М.Ляпунова) с вероятностью, сколь угодно близкой к единице, можно утверждать, что при достаточно большом объеме выборки и ограниченной генеральной дисперсии выборочные обобщающие показатели (средняя, доля) будут сколь угодно мало отличаться от соответствующих генеральных показателей.

Таким образом, величина предельной ошибки выборки может быть установлена с определенной вероятностью.

Значения функции Ф(1) при различных значениях ( как коэффициента кратности средней ошибки выборки, определяются на основе специально составленных таблиц. Приведем некоторые значения*, применяемые наиболее часто для выборок достаточно большого объема ( n>= ЗО):

t 1,000 1,960 2,000 2,580 3,000

Ф(t) 0,683 0,950 0,954 0,990 0,997

Предельная ошибка выборки отвечает на вопрос о точности выборки с определенной вероятностью, значение которой определяется коэффициентом (в практических расчетах, как правило, заданная вероятность не должна быть менее 0,95). Так при t = 1 предельная ошибка составит .

Следовательно, с вероятностью 0,683 можно утверждать, что разность между выборочными и генеральными показателями не превысит одной средней ошибки выборки. Другими словами, в 68,3% случаев ошибка репрезентативности не выйдет за пределы ± . При t=2 с вероятностью 0,954 она не выйдет за пределы ±2 , при t = 3с вероятностью 0,997 - за пределы ±3 и т.д.

Выборочное наблюдение проводится в целях распространения выводов, полученных по данным выборки, на генеральную совокупность.

Одной из основных задач является оценка по данным выборки исследуемых характеристик (параметров) генеральной совокупности.

Предельная ошибка выборки позволяет определить предельные значения характеристик генеральной совокупности и их доверительные интервалы.

При проектировании выборочного наблюдения с заранее заданным значением допустимой ошибки выборки очень важно правильно определить численность ( объем ) выборочной совокупности, которая с определенной вероятностью обеспечит заданную точность результатов наблюдения. Формулы для определения необходимой численности выборки п легко получить непосредственно из формул ошибок выборки:

для средней количественного признака

для доли (альтернативного признака)

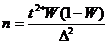
Эти формулы показывают, что с увеличением предполагаемой ошибки выборки значительно уменьшается необходимый объем выборки.

Для расчета объема выборки нужно знать дисперсию. Она может быть заимствована из проводимых ранее обследований данной или аналогичной совокупности, а если таковых нет, тогда для определения дисперсии надо провести специальное выборочное обследование небольшого объема.