Дать определение функции распределения случайного вектора.
Функция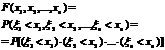 
называется n-мерной ФР случайного вектора 
.
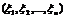Перечислить основные свойства многомерной функции распределения.
1) неубывающая функция по каждому аргументу.
2) непрерывна слева по каждому аргументу.
3) 
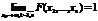
(если все xk®¥).
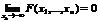
(если хотя бы один xk®¥).
4) "(a1,a2,b1,b2):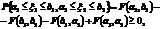 
a для n-мерного параллелепипеда аналогично, по формуле расширенного сложения вероятностей
Дать определение частного распределения.
Распределение любого подмножества случайных величин, полученных из исходного вектора, называется частным распределением.
Как найти частное распределение с помощью многомерной функции распределения?
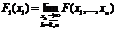
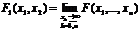
Перечислить основные виды случайных векторов.
Дискретные, непрерывные, смешанные.
Что такое «матрица распределений»? Какие у неё свойства?
Матрицей распределения называется матрица вида:
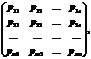
где m – число случайных величин в векторе, а e – число принимаемых значений.
Свойства:
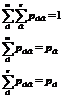
Как получить частное распределение дискретной случайной величины?
Просуммировать элементы матрицы распределений по переменным, не входящим в частное распределение
Как определяется плотность вероятностей многомерных непрерывных случайных величин?
Если существует такая функция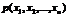 
, что при любых 
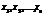имеет место равенство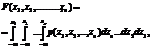 
, то эта функция называется плотностью распределения вероятностей случайного вектора.
Перечислить основные свойства плотности вероятностей СВ
1. p(x1,x2…xn)³0.
2. Вероятность попадания точки (x1,x2,…,xn) в некоторую область G равна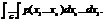 
Для элементарного параллелепипеда:
P(xk<xk £xk+dxk, k=1…n)@
@p(x1,x2…xn)dx1 dx2 dxn.
Как получить частные распределения для непрерывных случайных величин?
Проинтегрировать в бесконечных пределах плотность вероятности по переменным, не входящим в частное распределение
Дать определение условного закона распределения.
F(x|B)=P(x<x|B) – условная функция распределения СВ при условии B.
Как определяется условное распределение для дискретных СВ?
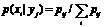
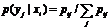
p(xi|yj)=pij/pj
Как определяется условное распределение для непрерывных СВ?.
p(x2,…xn|x1=X1)= p(x2,…xn)/p(x1)]|x1=X1 – условная плотность распределения при x1=X1.
Дать общее определение независимых СВ.
(x1,x2,…,xn) – независимы Û
"(x1,x2…xn)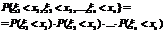 
Сформулировать условие независимости дискретных СВ.
(x1,x2,…,xn) – независимы Û
"(x1,x2…xn)
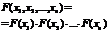
Сформулировать условие независимости непрерывных СВ.
1. (x1,x2,…,xn) – независимы Û
"(x1,x2…xn)
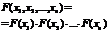
2. (x1,x2,…,xn) – независимы Û "(x1,x2…xn)
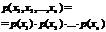
ФУНКЦИОНАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН.
130. Сформулировать задачу преобразования СВ.
По ФР F(x1,x2,…xn) совокупности СВ (x1,x2,…,xn) определить ФР F(y1,y2,…yk) величин h1=f1(x1,x2,…,xn),h2=f2(x1,x2,…,xn),…, hk=fk(x1,x2,…,xn)
131 Привести общий подход к решению задачи преобразования случайной величины
Искомая функция распределения определяется равенством
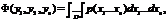D: {fi(x1,x2,…,xn)<yi, i=1..k}
В случае дискретных СВ решение даётся с помощью n-мерной суммы, также распространённой на область D.